數學愛好者 說,一個問題或定理的文本越短,它的解或證明越長,這個問題或定理就越漂亮。數學哲學家和歷史學家說,定理(作為猜想)被證明的時間越長,它對數學的發展以及對數學本質和基礎的探究就越重要。
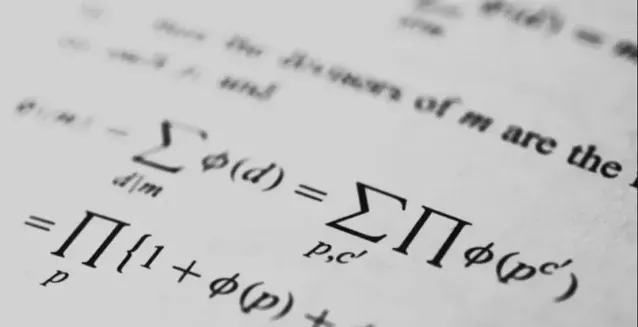
數學史證明他們在這方面是正確的。為了解決這些猜想,數學家們已經掙紮了幾十年,甚至幾百年,幾千年。他們被敦促把現有的不同性質、結構和語言的數學理論聯系起來,甚至創造出比這些猜想更復雜的新理論。隨著新的聯系、結構、概念框架 和內容的增加,它們促進了數學本身和科學的適用性的增加。
這篇文章,我列出了10個基於基礎數學 的猜想——即在基礎代數、數論、歐幾裏得幾何 和基本幾何拓撲中。這些猜想都是經過至少幾十年才被證明。
Abel-Ruffini定理 (25年)

也被稱為阿貝爾不可能定理,它表明五次或更高次的一般多項式方程式 不存在一般代數解(即根式解)。該猜想起源於1799年高斯的研究,同年保羅·魯菲尼首次嘗試解決該猜想。然而,魯菲尼的解對於當時的偉大數學家(包括柯西 )來說並不是令人信服的,因為使用的激進式的定義是不完整的。
N. H.阿貝爾 被認為是該猜想的證明者(1824年)。他的證明是基於伽羅瓦理論 的一些結果;然而,這個理論在證明的時候還沒有具體化。幾年後,在J.劉維爾 的合著下,伽羅瓦的理論發表了,並被公認為在方程式理論方面帶來了重大發現。
1963年,V. Arnold提供了Abel-Ruffini定理的拓撲 證明,奠定了拓撲伽羅瓦理論的基礎。
希爾伯特 的第17個問題(27年)
希爾伯特在1900年提出了著名的「23個數學問題」,其中第十七個問題是:
給定一個只在實數上取非負值的多變量多項式 ,這個多項式能被表示為有理函數 的平方和嗎?
這個問題起源於1885年H. Minkowski(閔考斯基 )的博士論文答辯,他認為存在著實多項式,它們在整個R^n 上是非負的,不能寫成實多項式的有限平方和。
希爾伯特在1893年解決了n = 2的特殊情況,E. Artin在1927年用有序體 的Artin- schreier理論肯定地解決了一般問題,並套用於代數群理論和模型理論。
費馬小定理 (43年)

這個猜想最早是由P·德·費馬在1640年寫給他朋友的信中提出的,它說,如果p是質數 ,那麽對於任何整數a,整數a^p - a是p的倍數。
在組合、多項式、動力系統 、模運算或群論項中,這個定理得到了一些證明。歐拉 在1736年首次發表了一個證明(用模運算 )。然而,在1683年之前,萊布尼茨 在一份未發表的手稿中留下了同樣的證明。該定理是數論的一個基本結論,是一個重要的質數檢驗。這個定理的一個直接推廣是數論中的歐拉定理 。這一定理最相關的理論套用是在群論中;至於實際套用,其中一個是密碼學 。
龐加萊猜想(98年)
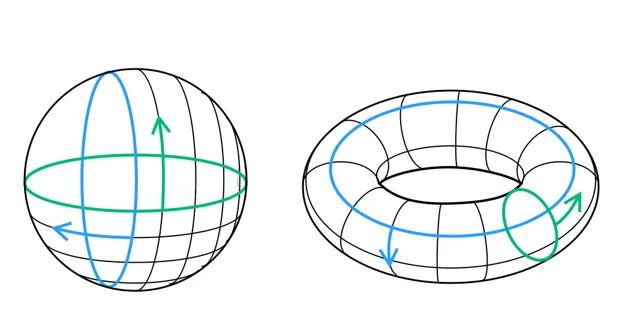
在拓撲學中,龐加萊猜想 是一個描述3維球(在四維空間包圍單位球的超球)的命題,它說每一個單連通的、封閉的3維流形與3維球是同胚的。
換句話說,對於一個局部看起來像三維空間,但是連線的空間,有限的大小,沒有任何邊界的空間,如果這樣的空間具有空間中的每一個環都可以連續地收緊到一個點的特性,那麽它必然是一個三維球體。
亨利·龐加萊 在1904年提出了這個猜想,並在2000年被評為千禧年獎問題之一。在20世紀50年代和60年代,其他數學家嘗試證明這個猜想。
1958年,R. H. Bing證明了Poincaré猜想的一個弱版本:如果一個緊湊的3維流形的每個簡單閉曲線 都包含在一個3維球中,那麽這個流形與3維球是同胚的。
俄羅斯數學家佩勒曼以咸美頓 的裏奇流 理論為基礎,利用Cheeger、Gromov和Perelman自己在度規空間上的結果,提出了一個完整的解決方案。該解決方案在2002年至2003年間在網上釋出了三份預印本 ,並在2006年進行了審查和確認。
佩勒曼因其工作而被授予費斯獎章。龐加萊猜想屬於代數拓撲 的早期歷史。將該猜想推廣到更高維度(已被證明)與黎曼幾何 中的變形概念有關,對萬有重力和宇宙學具有啟示和套用。
四色定理 (124 年)
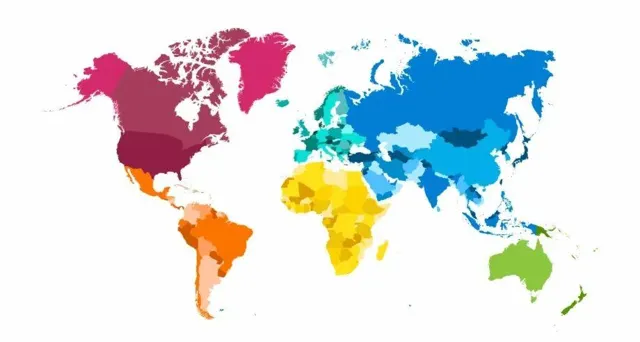
該定理指出,四種顏色足以為任何地圖上色,使兩個相鄰的區域不會共享相同的顏色。這個猜想是由法雷迪 ·格思裏在1852年向他的教授、數學家奧古斯都·德·摩根 提出的,後者將這個猜想公之於眾,並對其解決方案做出了貢獻。
在第二階段,數學家們專註於尋找技術,將復雜的地圖簡化為一組可測試的可分類案例。最初,這個集合被認為包含將近9000個成員,所以數學家們求助於電腦技術來編寫可以為他們做測試的演算法。
1976年,阿佩爾 和哈肯將測試問題簡化為1936個構型,並在電腦的幫助下實作了四色猜想 的完整解決方案。該定理在圖論中得到了證明,歐拉公式 起到了關鍵作用;然而,隨著時間的推移,射影幾何 、結論、拓撲學和組合學對證明做出了貢獻。
Catalan猜想(158年)

數學家 Catalan在1844年推測,8和9是唯一的 連續冪, 即
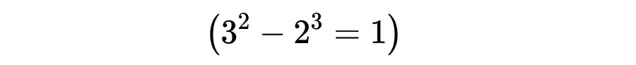
換句話說,(8,9)是方程式x^p - y^q =±1的唯一 非平凡解。 早在Catalan前500年,Levi ben Gerson就已經提出,平方數和3次方數相差為1的唯一滿足條件的是8和9。Hyyrő和馬可夫斯基證明了不存在三個連續的冪。蒂伊德曼在1976年指出,如果猜想不成立,可能只有有限數量的例外。
M. Mignotte在1999年證明,如果存在非平凡解 ,則p < 7.15 x 10^11和q < 7.78 x 10^16。羅馬尼亞 數學家P. Mihăilescu於2002年在發給多位數學家的手稿中解決了該猜想,並於2004年發表。該解利用了切圓場理論和伽羅瓦模。Catalan 猜想的推廣套用於復數理論。其他的套用是在伽羅瓦群理論中。
費馬大定理 (358年)
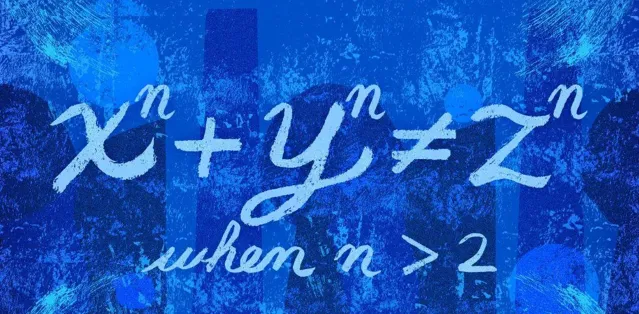
費馬在1637年提出的猜想說,對於任何大於2的整數n,都不存在a, b, c這樣的正整數滿足a^n + b^n = c^n。這是數學史上最著名的定理之一,它可以用多種方法等價地表達出來,無論是在數論中還是在橢圓曲線理論 中。
費馬只是在n = 4的特殊情況下證明了這個猜想;然而,這產生了一個重要的簡化,即充分證明指數 n為質數 的猜想。然後,數學家們花了350年的時間來尋找一個證明,他們中的許多人都取得了進展。
在費馬的部份證明之後的兩個世紀裏,這個猜想只在質數 3、5和7上得到了證明。在19世紀中葉,E. Kummer證明了所有 正則質數 都是如此。最後的證明是由A.懷爾斯在1995年提出的,他用伽羅瓦表示代替了橢圓曲線。這一證明為他帶來了2016年的阿貝爾獎 。在尋找解的過程中,我們發現了橢圓曲線和模形式 這兩個完全不同的數學領域之間的聯系。這個問題及其解決方法促進了代數數論 的發展和模性定理的證明。
開普勒猜想(403年)

1611年,天文學家約翰內斯·開普勒 提出了這一猜想,該猜想與三維空間中的球體堆積有關:它說,填充空間的同等大小的球體的平均密度,都比不上立方體緊密堆積和六邊形緊密堆積的球體的平均密度。高斯在1831年證明,如果球體排列在一個規則的晶格中,這個猜想是正確的。
1900年,希爾伯特將該猜想列入了他著名的23個未解數學問題清單 中。1953年,托特 表明,確定所有排列的最大密度的問題可以簡化為有限數量的計算。這意味著,在一台足夠快的電腦的幫助下,窮竭證明是可能的。根據這個想法,黑爾斯將線性規劃方法 套用到5000多個球體構型的函數上,並在1998年宣布他的證明已經完成。
該證明還廣泛地依賴於全域最佳化理論和區間演算法的方法。這對黑爾斯來說還不夠。2014年,他和21名合作者一起完成了為開普勒猜想尋找正式證明的專案,該專案可以透過自動證明檢查軟件進行驗證。雖然開普勒猜想 看起來像一個娛樂數學問題,但它與其他涉及各種最佳化模型的幾何拓撲問題有關聯。
蜂窩猜想 (2035年)

這個猜想是迄今為止等待證明時間最長的猜想,它具有實際套用和哲學意義。它說正六邊形 網格是把一個表面劃分成面積相等且總周長最小的區域的最好方法。它也可以用二維空間中具有光滑曲線的有限圖 來表示。這個問題的起因還不清楚;馬科斯 ·特倫提烏斯·瓦羅在公元前36年左右的一篇文章中提到過它;然而,據推測,齊納多魯斯更早的作品【等距圖】(約公元前180年)可能提到過它。
同樣是黑爾斯 在1999年提供了證據。證明的關鍵引理是周長面積的「等周」估計,證明是基於有限簇的縮減。該定理及其推廣在最佳化空間、物理結構和材料浪費方面有直接的套用,例如在建築方面。將該定理推廣到描述蜜蜂蜂巢形狀的三維空間中,成為科學哲學 中爭論的話題。
因為在物理上,它回到了前進演化的事實,六邊形的形狀。當蜜蜂為一個給定的蜂巢消耗最少的蜂蠟時,科學哲學家們就這一事實的解釋性質提出了幾個問題:這是一種真正的數學解釋 ,還是生物學解釋,還是兩者的結合?蜜蜂(和一般的動物)是否具有由前進演化所提供的符合形式數學 的感性數學知識?為什麽蜜蜂「知道」這個猜想的真相,而人類卻要等上兩千多年才能證明呢?











