2023.5.5更新,這是老文章與最新的rwkv-rnn無關。寫的時候錯誤很多,請選擇性觀看
導言
眾所周知,現在transformer及其變種是NLP和CV領域已經殺瘋了。但其中最核心的self-attention機制因為其O(N2)的時間復雜度(二次依賴問題)被詬病。
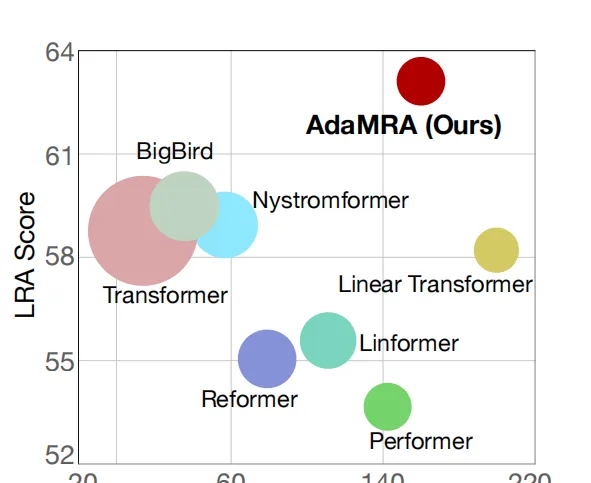
在不改變transformer block這個整體架構的前提下,現在學術界解決二次依賴問題的主要是兩個思路。一種是實作self-attention的線性化。這方面的工作是很多的,比如Performer[5]、Reformer[6]、Linformer[7]、Nyströmformer[9]、AdaMRA[10]等。關於這部份工作更多的內容大家可以在蘇劍林的網誌中了解到[8].雖然關於線性attention的工作很多,但參考AdaMRA[10]論文的圖。只有Nyströmformer[9]和AdaMRA[10]相較於Transformer能獲得速度和效果的雙重提升,其他的大多需要付出效果的代價才能獲取一定的速度提升。但就是這哥倆由於用了平均池化作為特征聚類,因此無法mask未來資訊從而喪失了自回歸的能力。因此透過替換線性attention從而提升transformer速度這一思路是必須付出代價的。
另一種思路將self-attention換成其他線性復雜度的部件。比如前段時間谷歌發現用膨脹摺積取代self-attention也能取到不錯的效果[1]。而在CV領域殺瘋的MLP-Mixer[2],兼具CV和NLP能力的gMLP、aMLP,[3]MLP-Mixer的NLP版本Synthesizer[4]。但都有或多或少的缺點,就比如Synthesizer和gMLP在NLP領域相較於self-attention還是差了點的。而aMLP雖然效果好了吧,但其實還是要用到self-attention,提速的目的還是沒達到。不過今年暑假那會,蘋果提出的AFT模型[11]號稱自己是最快的transformer模型。

上述是標準AFT的公式,其中σ是sigmoid函數,QKV就是sefl-attention的那一套,w是一個訓練出來的參數矩陣。不難看出AFT是透過點乘的方式實作的註意力,在做自回歸時只需要對W矩陣進行mask即可。並且W矩陣是內建位置資訊的,不僅解決了部份線性attention不能做自回歸的問題,還順便把transformer裏位置編碼的問題給解決了。可以說AFT實作了一舉三得。但成也蕭何敗也蕭何,W矩陣是AFT成功的核心也是AFT的最大缺點。一般來說W應該是一個[max_len,max_len]大小的方陣。換而言之AFT所能處理的文本長度受限於W矩陣的大小,如果想要處理一萬字的長文本,W矩陣的參數量就快趕上Bert了。為了解決這個問題,下面該本文的主角RWKV出場了。RWKV的原文在https:// zhuanlan.zhihu.com/p/39 7985790 ,不過原文實在過於簡短了不便閱讀和理解。因此筆者寫了此文介紹一下RWKV是怎麽實作魚和熊掌兼得的。
RWKV
整體結構 RWKV的整體結構依然采用的是transformer block的思路,其整體結構如圖所示。相較於原始transformer block的結構,RWKV將self-attention替換為Position Encoding和TimeMix,將FFN替換為ChannelMix。其余部份與transfomer一致的。

Position Matrix RWKV采用的位置編碼類似於AliBi編碼[12]的形式。原文作者並沒有給他的位置編碼命名,為了便於介紹參考該位置編碼主要考慮距離衰減的特性,本文將其命名為distance編碼。對於第i個head的第j個token而言,其位置編碼如下述公式所示。其中n head表示頭的數量,max _len表示為所允許的最大長度。
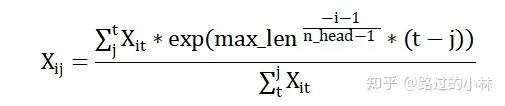
目前學術界的主流觀點是RNN結構是天然的時序結構,不需要transformer模型必須的位置編碼。而如果我們檢視RNN的計算流程,可以發現RNN只考慮到當前token及之前的資訊,而隨著距離的延長前面的資訊會逐漸減少。而distance位置編碼便是參考RNN時序特點所設計的。
不過RWKV模型中,不會直接對輸入的X進行上述計算。而是得到類似AFT中的W矩陣參與後續Time-Mix計算。其中W矩陣的形狀為[n_head,seq_len,seq_len]。因此對於W矩陣中的而言,其數值如下述公式所示。

從這裏不難看出,AFT中的W矩陣在RWKV中是透過公式得到而不是訓練得到的,因此解決了AFT中無法解決長文本,或解決長文本時參數爆炸的問題。
當然,在處理的任務文本長度有限的情況下。比如機器轉譯,或者是RWKV目前套用的ai寫小說這類套用場景。在這類套用場景中,由於不會面臨長文本的情況,因此可以為W矩陣添加更多的位置資訊。參考公式如下

其中和分別為形狀[n_head,seq_len,1]和[n_head,1,seq_len]的向量,在初始化時為全1矩陣。即將作為W矩陣的初始化。結合該步後,在形式上W矩陣融合了distance編碼中的距離資訊與相對資訊。
值得註意的是,原作者是設計distance編碼時專門設計了一個不考慮位置資訊衰減的頭。即該頭的W矩陣是一個全一的下三角矩陣。
Time-shit 在介紹TimeMix之前,要先介紹一下RWKV所使用的Time-shit技巧。
原文:https:// zhuanlan.zhihu.com/p/39 9480671
Time-shiit是原作者提出的一種幾乎零成本提升模型效果的trick,實作程式碼如下所示。
Torch實作
C=x.shape[-1]
self.time_shift = nn.ZeroPad2d((0,0,1,0))
x = torch.cat([self.time_shift(x)[:, :-1, :C//2], x[:, :, C//2:]], dim = -1)
Keras實作
d=K.shape(x)[-1]
x=K.concatenate(K.temporal_padding(x,(1,0))[:,:-1,:d//2],x[:,:,d//2:])
可以看出不論哪個框架也就兩行就能實作了,為了便於讀者理解。假設存在一個3x4的矩陣。

在經過time-shift後變為

其實就相當於插入一個小的RNN,實驗表明簡單的trick能讓模型的更快更好地收斂。
TimeMix TimeMix是RWKV中用於代替self-attention的部份,基於AFT的基礎上做出改進兼具了線性的速度和較好的效能。在進行該步前,需要對輸入的x進行time-shift。
同self-attention中的QKV矩陣一樣,RWKV中也有對應的RKV矩陣。對與輸出矩陣中第i個頭的第j個token而言計算步驟如下所示。
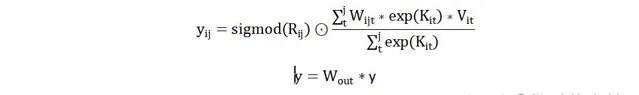
這其中是一個[hiden_size,hiden_size]大小的方陣,與常規attention一樣用於最後的輸出。而是一個[seq_len,hiden_size]大小的矩陣,其作用筆者猜測應該是類似於bias的作用。
ChannelMix ChannelMix 是RWKV中用於替代FFN的部份。類似於tiny attention之於attention。ChannelMix本質上來說是一個tiny TimeMix。
在進行該步計算前,和TimeMix一樣要先進行一次time-shift。隨後依然要計算出RKV矩陣和W權重。不過有所不同的是在這一步中假設輸入x的維度是embed_size,則R的維度應和X相同。KV的維度是使用者所自訂的hidden_size,W的形狀為[hidden_size,embed_size].
透過設定較小的hidden_size可以實作一個tiny版TimeMix,能在對效能影響較小的情況下實作提速。當hidden_size==embed_size時,可以看作一個不考慮位置資訊和歸一化的TimeMix或者看作點乘式的FFN。
具體計算公式如下所示
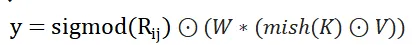
總結 本文介紹了一種魚和熊掌兼得的模型。既能和AFT一樣兼具通用性和高效,distance位置編碼的設計使得模型也具備面對超長文本的能力。
實際實驗效果可以去看原文的內容,本文只對其結構進行介紹。但總體而言,筆者測試過基於GPT的ai寫小說和基於RWKV的ai寫小說。相比較而言,RWKV的寫出來的文章會更流暢,並且在訓練時收斂速度頁更快。
參考文獻
[1] Are Pre-trained Convolutions Better than Pre-trained Transformers https:// arxiv.org/pdf/2105.0332 2.pdf
[2] MLP-Mixer: An all-MLP Architecture for Vision https:// arxiv.org/pdf/2105.0160 1.pdf
[3] Pay Attention to MLPs https:// arxiv.org/pdf/2105.0805 0.pdf
[4] Synthesizer: Rethinking Self-Attention in Transformer Models https:// arxiv.org/abs/2005.0074 3
[5] Rethinking Attention with Performers https:// arxiv.org/abs/2009.1479 4
[6] Reformer: The Efficient Transformer https:// arxiv.org/abs/2001.0445 1
[7] Linformer: Self-Attention with Linear Complexity https:// arxiv.org/abs/2006.0476 8
[8] 線性Attention的探索:Attention必須有個Softmax嗎? https:// spaces.ac.cn/archives/7 546
[9] Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention https:// arxiv.org/abs/2102.0390 2
[10] Adaptive Multi-Resolution Attention with Linear Complexity https:// arxiv.org/abs/2108.0496 2
[11] An Attention Free Transformer https:// arxiv.org/abs/2105.1410 3
[12] Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation
https:// arxiv.org/abs/2108.1240 9











