來一個不需用到傅立葉級數的方法
我們考慮如下積分 I=\int_0^1\int_0^1\frac{1}{1-xy}dxdy ,有如下計算方法
方法一:
\begin{align} I&=\int_0^1\int_0^1\sum_{n \ge 0}(xy)^ndxdy=\sum_{n \ge 0}\int_0^1\int_0^1x^ny^ndxdy\\ &=\sum_{n \ge 0}\left(\int_0^1x^ndx\right)\left(\int_0^1y^ndy\right)=\sum_{n\ge0}\frac{1}{n+1}\cdot\frac{1}{n+1}\\ &=\sum_{n=1}^{\infty}\frac{1}{n^2} \end{align}
方法二: 考慮座標變換 s=\frac{y+x}{2},t=\frac{y-x}{2} ,原積分區域為邊長為1的正方形,變換後逆時針旋轉45°再縮小為原來的 \frac{1}{\sqrt{2}} 得到新的積分區域
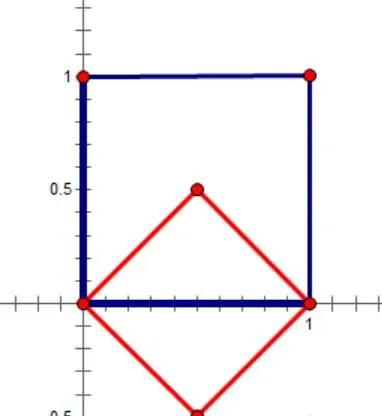
由 x=s-t,y=s+t 有 \frac{1}{1-xy}=\frac{1}{1-s^2+t^2} ,再由 \mathbb{Jacobi} 行列式可得 dxdy=2dsdt ,註意到積分區域的對稱性我們有 \begin{align} I&=4\int_0^{\frac{1}{2}}\left(\int_0^s\frac{1}{1-s^2+t^2}dt \right)ds+4\int_{\frac{1}{2}}^1\left(\int_0^{1-s}\frac{1}{1-s^2+t^2}dt \right)ds\\ &=4\int_0^{\frac{1}{2}}\frac{1}{\sqrt{1-s^2}}\arctan\frac{s}{\sqrt{1-s^2}}ds+4\int_{\frac{1}{2}}^1\frac{1}{\sqrt{1-s^2}}\arctan\frac{1-s}{\sqrt{1-s^2}}ds\\ &=2\arctan^2\frac{s}{\sqrt{1-s^2}} \Bigg|_0^{\frac{1}{2}}-4\arctan^2\frac{1-s}{\sqrt{1-s^2}} \Bigg|_{\frac{1}{2}}^1\\ &=2\cdot\frac{\pi^2}{36}+4\cdot\frac{\pi^2}{36}\\ &=\frac{\pi^2}{6} \end{align}
綜上即證明了 \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}
還可以利用 \int_0^1\int_0^1\frac{1}{1-x^2y^2}dxdy 證明 1+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\cdots=\frac{\pi^2}{8}











