這道題看起來像是一道演算法題,本質上卻是披著豬皮的 消息理論 問題。解答這道題並不是我的目的,我的目的是用消息理論的思維來思考,達到觸類旁通,一通百通。
用消息理論去思考的另一個好處就是,消息理論給了這類問題的一個邊界,讓我們在邊界範圍內思考問題。很難想象,70多年前的 山農 已經用嚴格的理論證明為這類問題設定了一個極限,任何想逾越這個極限去解決問題的人最後都會被證明是徒勞的。
這也是理論武裝頭腦的好處,當別人還在嘗試是否有更優的解法時,你可以直接給出最優答案,用消息理論降維打擊。即使我可能暫時無法想出具體的方案,但我知道這類問題的一個理論極限在哪裏,沒有必要為超越極限做無用功。
所以,在解題之前我覺得有必要補充一下理論知識,讓我們了解一下消息理論中「 資訊熵 」。
資訊熵
1. 熱力學中的熵
熵 的概念最早起源於物理學,用於度量一個熱力學系統的無序程度,也就是系統混亂程式。
熵增定律 指出:
在一個孤立系統裏,如果沒有外力做功,其總混亂度(熵)會不斷增大熵增定律讓我們知道,如果將一杯熱水和一杯涼水倒在一起,並且不對水杯中的水做功,這杯水的冷熱分子最終一定呈最混亂的分布,也就是最終整體溫度均勻分布,絕對不會出現冷熱水分層的現象。
如果把宇宙當成一個孤立系統,那麽宇宙一定是從有序變為無序混亂的狀態,當宇宙的熵達到最大值時,宇宙中的其他有效能量已經全數轉化為熱能,所有物質溫度達到熱平衡。這種狀態稱為熱寂。這樣的宇宙中再也沒有任何可以維持運動或是生命的能量存在。
2. 消息理論中的熵
在消息理論中,熵的概念和熱力學中是類似的,描述的是「 資訊的不確定程度 」。
所以資訊中的不確定性類似於熱力學中系統的混亂程度。
所以也就是說,資訊的不確定程度越大,資訊熵也就越大。那什麽樣的資訊不確定程度大呢?
比如拋一枚硬幣,如果我來猜正反的話,那麽我基本只能靠瞎蒙,因為不確定程度很大,正反的概率都是0.5。對於拋一次硬幣猜正反這類事件來說,它的不確定程度很大,資訊熵也很大。
如果中國男足和巴西男足比賽,讓我來猜勝負,那麽我幾乎可以斷言,巴西隊一定會贏。也就是巴西隊和中國隊勝負這個事件的不確定程度很小,資訊熵也就很小。
如果比賽後巴西隊真的贏了,那麽這條資訊的資訊量幾乎為零,因為這條資訊幾乎沒有降低資訊的不確定度。
上面提到了 資訊熵、資訊、資訊量 ,它們之間的比較如下:
上面都只是定性的分析,山農把隨機變量 X 的熵值 Η定義如下,其值域為{ x 1, ..., xn }
\mathrm{H} (X)=-\sum _{{i}}{{\mathrm {P}}(x_{i})\log _{b}{\mathrm {P}}(x_{i})}
b是 對數所使用的底。當 b = 2,熵的單位是 bit 。
P為 X 的概率質素函數(probability mass function),我們可以理解為事件xi 發生的概率。
公式看起來可怕,其實非常簡單。
讓我們用拋硬幣來舉例,「拋一次硬幣是正面」這個隨機變量X的 資訊熵 為
\mathrm{H} (X)=-(\frac{1}{2}log _{2}\frac{1}{2} + \frac{1}{2}log _{2}\frac{1}{2}) = -log_{2}\frac{1}{2}=1
也就是拋一次硬幣是正面這個事件的資訊熵只需要1 bit,也就是只需要用1位的二進制數就可以表示這個資訊大小。
題目的簡化版本
在我們學習了資訊熵的知識以後,讓我們再來看題目。原題其實略微復雜一些,先將題目簡化一下。
1000桶水,其中一桶有毒,豬喝毒水後會在15分鐘內死去,想用15分鐘內找到這桶毒水,至少需要幾頭豬?上面這道題其實也是當年google的一道面試題,只不過面試題中的小白鼠在這裏被替換成了豬。原題是多次試驗問題,簡化後的版本是單次試驗,更容易看到這道題的本質。於是我們利用上面介紹的資訊熵的知識來求解一下。
首先,」 1000桶水其中有一桶有毒 「這個隨機變量X的 資訊熵 為
\mathrm{H} (X)=-log _{2}\frac{1}{1000} =9.966
1只豬喝水以後的要麽活著,要麽死去,一共有兩種狀態,所以」1只豬喝完水以後的狀態「這個隨機變量Y的資訊熵為
\mathrm{H} (Z)=-(\frac{1}{2}log _{2}\frac{1}{2} + \frac{1}{2}log _{2}\frac{1}{2}) = -log_{2}\frac{1}{2}=1
n只豬喝完水會有 2^n 種狀態,即"n只豬喝完水以後的狀態"這個隨機變量Y的資訊熵為
\mathrm{H} (Y)=-\sum _{{i=1}}^{2^n}{\frac{1}{2^n}}{\log _{2}{\frac{1}{2^n}}}=-\log _{2}{\frac{1}{2^n}}=n
所以,按照題目要求,如果至少需要n頭豬能夠找到這桶毒水,那麽隨機變量Y的資訊熵必須要大於隨機變量X的資訊熵,也就是
H(Y) >= H(X) ,也就是 n >= 9.966,即 n = 10
當我們用資訊熵算出來了n的最小值以後,我們就可以堅信,理論上n=10一定是最優解,任何想方設法想找到小於10的值都是徒勞的。
其實,上面的資訊熵計算的簡化版本可以寫成如下更好理解的形式
2^n \ge 1000
同樣可以解得 n = 10 ,雖然形式簡單,但我們一定要記住它背後的原理是資訊熵。
至於到底采用什麽方案,這涉及到術的層面,即使我們暫時想不到,我們也會有努力的方向,並且知道努力的邊界在哪裏,不會做類似尋找永動機的事情。
下面我們來看下圖具體的方案
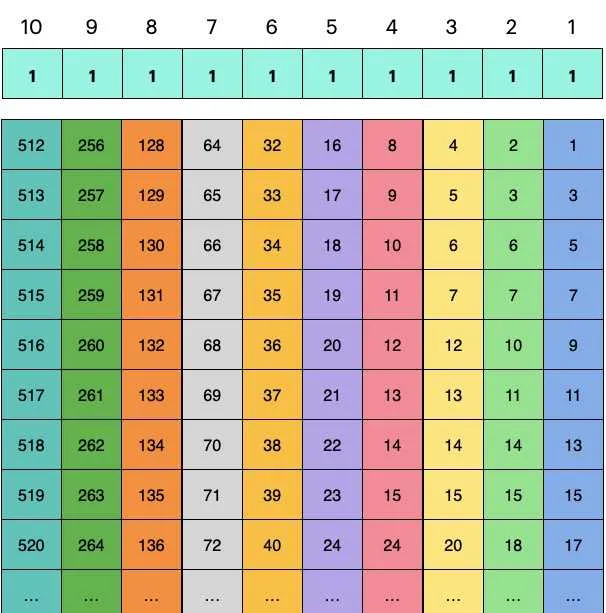
我們將1000桶水按照2進制編碼,如上圖第一行,需要10位二進制數。於是有
於是,我按照如下方案讓豬進行喝水,如上圖所示:
如果15分鐘後1,3,5號豬被毒死,那麽對應的二進制編碼就是00000 10101b,也就是21號水桶有毒。更一般的,豬死的任何一種排列方式都對應了二進制的唯一編碼。
這裏為什麽采用二進制的編碼方式?
首先,我們要理解為什麽電腦內部運算都采用二進制的方式,這是因為開關電路在電腦中實作起來非常簡單,而開關兩種狀態正好對應了二進制的0和1。老式的電腦都是用繼電器的開關實作的,而現代電腦也是利用邏輯電路的通斷實作高低電壓來表示0和1。所以電腦內部的運算其實都是將其轉化為二進制再進行運算的。
而豬的生死正好對應了電腦中的開關電路,所以我們這裏采用二進制進行編碼。
而原題目多次試驗的情況就不能采用二進制編碼了。
原題目
1000桶水,其中一桶有毒,豬喝毒水後會在15分鐘內死去,想用一個小時找到這桶毒水,至少需要幾頭豬?有了前面簡化的版本的理解,我們容易得知
」 1000桶水其中有一桶有毒 「這個隨機變量X的 資訊熵 為
\mathrm{H} (X)=-log _{2}\frac{1}{1000} =9.966
而對於豬的狀態就不太一樣了,我們可以想象一下,一只豬在一個小時內會有幾種狀態?
- 在第0分鐘的時候喝了一桶水以後,第15分鐘死去。
- 第15分鐘依然活著,喝了一桶水以後,第30分鐘死去。
- 第30分鐘依然活著,喝了一桶水以後,第45分鐘死去。
- 第45分鐘依然活著,喝了一桶水以後,第60分鐘死去。
- 第45分鐘依然活著,喝了一桶水以後,第60分鐘依然活著。
可見,1只豬1個小時以後會有5種狀態,所以」1只豬1個小時後的狀態「這個隨機變量Z的資訊熵為
\mathrm{H} (Z)=-( 5 \times \frac{1}{5}log _{2}\frac{1}{5} ) = log_{2}5=2.3219
n只豬1個小時後會有 5^n 種狀態,即"n只豬1個小時以後的狀態"這個隨機變量Y的資訊熵為
\mathrm{H} (Y)=-\sum _{{i=1}}^{5^n}{\frac{1}{5^n}}{\log _{2}{\frac{1}{5^n}}}=-\log _{2}{\frac{1}{5^n}}=n \log_{2}{5}=2.3219n
所以,按照題目要求,如果至少需要n頭豬能夠找到這桶毒水,那麽隨機變量Y的資訊熵必須要大於隨機變量X的資訊熵,也就是
H(Y) >= H(X) ,也就是 n >= 9.966 / 2.3219 = 4.292,即 n = 5
事實上, 對於 n = 5來說,不僅可以檢測1000桶水,甚至檢測3000桶水都是沒有問題的。有興趣的童鞋可以試著計算一下 。
到此,山農給了我們一個理論極限,但是具體的方案還是需要我們自己進行構造。 得出n=5是依靠我們的理論功底,而得出具體的方案就是我們的工程水平了。
根據前面簡化版本的二進制編碼方式的思路,我們是不是可以利用豬的5種狀態構造一個5進制編碼方式呢?如下圖所示。

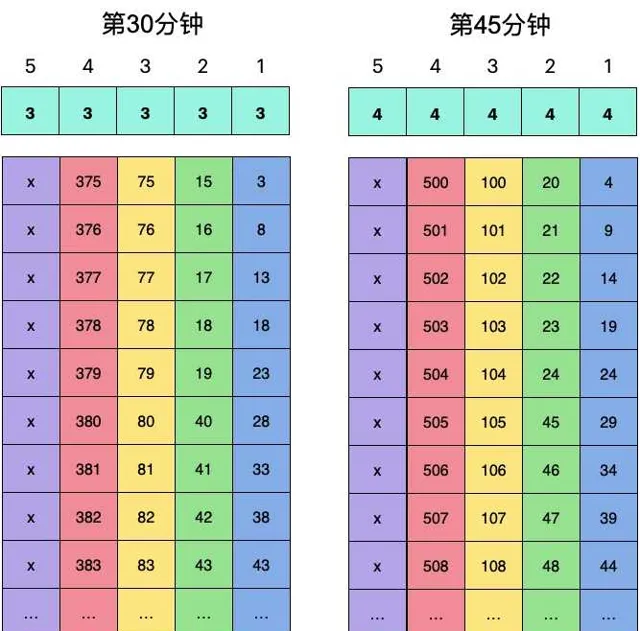
首先,將1000桶水按照5進制編碼的方式排列,如上圖所示,需要5位5進制數。
然後按照如下方案讓豬進行喝水,如上圖所示:
上面,豬的編號代表5進制編碼數碼所在的位數,1號豬代表最末位,5號豬代表最高位。而第幾分鐘死代表當前位數的權重,15分鐘死表示權重是1,30分鐘死表示權重是2,... ,60分鐘死表示權重是4,60分鐘依然活著表示權重是0。
如果1號豬第30分鐘死了,2號豬第15分鐘死了,3號豬第45分鐘死了,4,5號都活到了最後。則毒水對應的5進制編碼是
0 \times 5^4 + 0 \times 5^3 + 3 \times 5^2 + 1 \times 5^1 + 2\times5^0 = 82
也就是第82桶水有毒。
到此,這個問題從理論和工程上都給出了答案。資訊熵讓我們明確了工程上努力的方向並明確了那條不可逾越的鴻溝。
熵的拓展
前面提到了熱力學中的「熵增定律」,其實在社會中「熵」也有重要的意義。
對於國家來說,如果閉關鎖國,相當於一個孤立系統,就好比鴉片戰爭前的清政府,不與外界進行交流,也不進行貿易,也就相當於沒有能量的交換,最終的結果必定是「熵增」,即越來越混亂,越來越沒有效率。
所以必須保持對外開放的政策,與外界環境不間斷的交換。比如:與世界各國進行貿易往來,招商引資,引進競爭,這些都是「負熵」的表現。
對於企業也是同理,必須引進「負熵」,比如現代化的管理方式,先進的技術等等。否則,企業內部不了解外部經濟環境變化,也不了解終端使用者,只能是最終能量耗盡而亡。
最後,希望本篇回答讓你不僅了解了題目本身,更能知道消息理論在解決類似問題時給出的指導意義,讓我們具備自頂而下的思考方式,首先直擊問題本質,將現實問題抽象成數學或者其他已知問題,然後用理論給出答案的邊界,也明確的努力的方向和極限。接下來在工程上,保證在理論邊界內去嘗試,而不是一味地試圖超越理論極限,做無用功。
而常人的做法往往是先嘗試一種方案,發現應該還有最佳化空間,於是逐步最佳化,但是不知道努力的方向和邊界。
所以往往要麽在努力的過程中離邊界值還有很大距離的時候就放棄了,要麽就是試圖突破邊界而做無用功,要麽努力了一大頓最後才發現極限的最佳化提升空間也只有2%,不得不更換方案。
這可能也是高手與常人的區別,希望本文能讓大家了解這種自頂向下的思考方式。
2020-6-10號更新
看到評論中有很多對答案有疑問的,所以補充一下答疑,不一一回復了,謝謝。
1. 有的評論說,一只豬就夠,每隔兩秒鐘喝一次。
請參見題目詳情限制條件1
「1.一滴毒水足以導致一頭豬的死亡。死亡時間為15分鐘內不確定的某個時間點。」請仔細審題,不是恰好15分鐘,而是最長15分鐘。豬每隔兩秒喝一次即使死了也是無法區分哪桶水有毒的。
仔細審題很重要啊!
2. 為什麽題目中在計算豬的資訊熵時采用了等概率?
很抱歉,這個我在解釋的過程中忽略了。
首先要明確的是,豬在喝毒水的時候生和死的概率確實不一定是等概率的,這個是對的。
比如原題中,對於5號豬來說,因為它喝的水位於5進制的最高位上,所以它活的概率是 \frac{624}{1000} = 0.624 。
既然不是等概率,那正文中為什麽采用等概率的方式呢?這是因為在計算資訊熵的時候,我們考慮的是n只豬所能表達的最大資訊熵。
數學上可以證明,當隨機事件等概率發生的時候,資訊熵是最大的 。
題目要求最少n只豬,意思就是在最差情況下用n只豬也能找到毒水。而最差的情況就是每只豬生死的概率是相等的。
所以我們用等概率的方式求出最大資訊熵時最小的n,當n再小,最差情況下已經無法測出1000桶水了。
如果你覺得對你有幫助,請幫忙點贊,謝謝。











