你能求出 \vec{b}=\begin{bmatrix}2\\3\\4\end{bmatrix} 在 z 軸和 xy 平面的投影(projection)嗎?分別向 z 軸和 xy 平面做垂線,不難得出 \vec{b} 在 z 軸的投影 p_{1}=\begin{bmatrix}0\\0\\4\end{bmatrix} , \vec{b} 在 xy 平面的投影 p_{2}=\begin{bmatrix}2\\3\\0\end{bmatrix} 。前瞻性的多說一句,因為 z 軸和 xy 平面互為正交補餘,所以 p_{1} 和 p_{2} 正交,且 p_{1}+p_{2}=\vec{b} 。
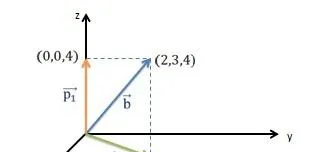
投影包含了兩層意思:
上面例子的投影空間分別是 z 軸和 xy 平面,它們太特殊,現在我們看看一般情況下如何求投影:
問題一:求 \vec{b} 在直線 \vec{a} 方向的投影。
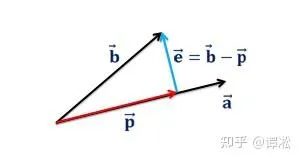
有一條過原點且沿著 \vec{a}=\begin{bmatrix}a_{1}\\a_{2}\\...\\a_{n}\end{bmatrix} 方向的直線,我們要求 \vec{b}=\begin{bmatrix}b_{1}\\b_{2}\\...\\b_{n}\end{bmatrix} 在這條直線的投影 \vec{p} 。因為 \vec{p} 和 \vec{a} 共線,所以 \vec{p}=x\vec{a} 。 求投影的關鍵就是要利用正交性: \vec{b}-\vec{p} 和 \vec{a} 正交。 \vec{b}-\vec{p} 是原向量和投影的差,代表誤差,通常用字母 \vec{e} 表示。從幾何角度我們就可以知道投影意味著 \vec{e} 和 \vec{a} 正交,即 \vec{a}\cdot\vec{e}=0 。根據正交關系立刻可以得出 \vec{a}\cdot (\vec{b}-\vec{p})=0\Rightarrow\vec{a} \cdot (\vec{b}-x\vec{a})=0\Rightarrow x=\frac{\vec{a}\cdot \vec{b}}{\vec{a}\cdot\vec{a}}=\frac{\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}} ,我們率先求出了系數 x , x 運算式中分子分母是兩個點乘,結果都是純量數碼,所以 x 也如我們所料是個數碼。那麽相應的投影 \vec{p}=\frac{\vec{b}\cdot\vec{a}}{\vec{a}\cdot\vec{a}}\vec{a} ,它和 \vec{a} 同方向,它是 \vec{a} 的 x 倍。事實上,投影還可以看作 \vec{p}=\frac{\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}}\vec{a}=(\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}})\vec{b} ,其中 \vec{b} 前面的部份 \frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}} 不再是數碼,而是個矩陣,記為 P ,即 \vec{p}=P\vec{b} ,求一個向量的投影,就是對這個向量進行線性變換,也就是用矩陣乘向量。投影矩陣 P 只和 \vec{a} 有關, P=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}} 。
我們看一個具體例子。將 \vec{b}=\begin{bmatrix}1\\1\\1\end{bmatrix} 投影到 \vec{a}=\begin{bmatrix}1\\2\\2\end{bmatrix} 所在直線,系數 x=\frac{\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}}=\frac{5}{9} ,投影 \vec{p}=x\vec{a}=\frac{5}{9}\begin{bmatrix}1\\2\\2\end{bmatrix} 。我們可以驗證一下 \vec{e}=\vec{b}-\vec{p}=\begin{bmatrix}\frac{4}{9}\\-\frac{1}{9}\\-\frac{1}{9}\end{bmatrix} ,\vec{e}\cdot \vec{a}=\begin{bmatrix}\frac{4}{9}\\-\frac{1}{9}\\-\frac{1}{9}\end{bmatrix}\cdot\begin{bmatrix}1\\2\\2\end{bmatrix}=\vec{0} , \vec{e} 與 \vec{a} 正交。
投影矩陣P=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}=\frac{1}{9}\begin{bmatrix}1\\2\\2\end{bmatrix}\begin{bmatrix}1&2&2\end{bmatrix}=\frac{1}{9}\begin{bmatrix}1&2&2\\2&4&4\\2&4&4\end{bmatrix} ,它是個對稱陣。 P 可以投影任何向量到 \vec{a} 所在直線,例如本例中 \vec{p}=P\vec{b}=\frac{1}{9}\begin{bmatrix}1&2&2\\2&4&4\\2&4&4\end{bmatrix}\begin{bmatrix}1\\1\\1\end{bmatrix}=\begin{bmatrix}\frac{5}{9}\\\frac{10}{9}\\\frac{10}{9}\end{bmatrix} 。
如果 \vec{b}=\vec{a} ,則有 x=1 ,向量投影到自身仍是它本身。如果 \vec{b} 和 \vec{a} 正交,那麽 \vec{b}\cdot\vec{a}=0 ,所以 x=0,\vec{p}=0 ,向量在與它正交方向的投影為0。如果 \vec{a} 變為 2\vec{a} , P 是不變的,因為直線仍然是那條直線,所以投影和投影矩陣都不會改變,這是合乎預期的(但 x 會改變)。 P^{2}=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}=\frac{\vec{a}(\vec{a}^{T}\vec{a})\vec{a}^{T}}{(\vec{a}^{T}\vec{a})^{2}}=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}=P , 再投影一次是不會改變投影的,這也符合常識。
問題二:求 \vec{b} 在以 a_{1},a_{2}..a_{n} 為基的子空間 S 的投影。
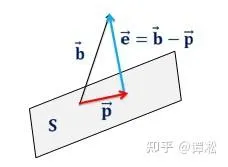
我們把 a_{1},a_{2}..a_{n} 作為矩陣 A 的列,這樣一來以 a_{1},a_{2}..a_{n} 為基的子空間 S 就是矩陣的列空間 C(A) , \vec{b} 在 C(A) 的投影 \vec{p} 是 C(A) 中的向量,自然可以表示成 Ax ,確定了 x 就知道了投影。 求解的關鍵依然是正交性:誤差 \vec{e}=\vec{b}-\vec{p} 與 S 中所有向量正交,等效於 \vec{e} 與 S 的基 a_{1},a_{2}..a_{n} 正交: \vec{a_{1}}^{T}\vec{e}=0,\vec{a_{2}}^{T}\vec{e}=0,...\vec{a_{n}}^{T}\vec{e}=0 , 用矩陣乘法表示為 A^{T}\vec{e}=A^{T}(b-Ax)=0 , \vec{e} 在 A 的左零空間中,我們通常覆寫為 A^{T}Ax=A^{T}b 。讓我們停留片刻消化一下這個方程式:本來 \vec{b} 不在 C(A) 中, Ax=b 無解;現在我們兩邊乘 A^{T} 改求 A^{T}Ax=A^{T}b ,這樣解得的 x 作為系數對 A 的列線性組合得到的 Ax 是 C(A) 內最「接近」 \vec{b} 的向量,也就是 \vec{b} 在 C(A) 的投影。
現在我們來求解。根據 A^{T}Ax=A^{T}b 解得 x=(A^{T}A)^{-1}A^{T}b , 進而得到投影\vec{p}=Ax=A(A^{T}A)^{-1}A^{T}b ,投影矩陣 P=A(A^{T}A)^{-1}A^{T} 。
細心的讀者一定會在 (A^{T}A)^{-1} 這裏停下來思考。 A^{T}A 是方陣,但它一定可逆嗎?事實上我們在之前的文章中一再的證明過一個結論: A^{T}A 和 A 有相同的零空間。 當 A 的列線性獨立, Ax=0 便只有 0 解,那麽 (A^{T}A)x=0 也只有零解,即 A^{T}A 可逆。換句話說, 只要 A 的列線性獨立,A^{T}A 就可逆。
投影矩陣 P=A(A^{T}A)^{-1}A^{T} 也頗具迷惑性。讀者或許會想起矩陣相乘然後求逆的公式 (A^{T}A)^{-1}=A^{-1}(A^{T})^{-1} ,然後得出 P=A(A^{T}A)^{-1}A^{T}=AA^{-1}(A^{T})^{-1}A^{T}=I ,向量在任意子空間的投影 P\vec{b}=I\vec{b}=\vec{b} ,這顯











