在日常生活中,我們常常使用相機APP幫助我們對照片進行美化處理,包括人物磨皮、美白、紅潤、亮眼、美牙等多種美化維度,也包括了虛擬試妝的效果等。想要打造自然美顏的效果,這背後離不開AI演算法。本文邀請到曠視演算法員師寧遠同學,來給大家分享一種實作簡單、效果很好的磨皮演算法以及對它的最佳化思路。
磨皮演算法
磨皮的基本方法
磨皮演算法的核心就是讓皮膚區域的像素變得平滑,過渡自然,這樣皮膚上的瑕疵就不容易察覺了,皮膚看起來十分光滑。這裏包括了兩部份演算法:1. 影像濾波演算法;2. 皮膚區域檢測演算法。整體的流程如下:
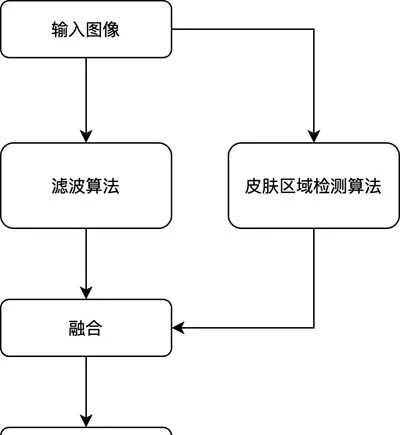
皮膚區域檢測可參考從AR口紅試妝了解人工智能試妝技術,此文不再贅述。
濾波演算法一般有兩類作用:一是讓畫面變得平滑甚至模糊,二是去除畫面中的噪點。在磨皮演算法裏主要的作用是過濾掉畫面中微小的瑕疵、讓顏色過渡更加平滑。其主要的思想是讓中心像素顏色和周圍像素顏色取加權均值,然後更新中心像素的顏色值。濾波視窗中的各像素權重有很多種選取方式,由此產生了多種濾波演算法。
常見的濾波演算法
常用的濾波方法有盒型濾波(如均值濾波)、統計排序濾波(如中值濾波)、高斯濾波和保邊濾波(如雙邊濾波)等。不同濾波演算法產生的效果會有很大區別。其中一些對去除噪點效果很好,如中值濾波;一些產生平滑的畫面效果,如均值濾波、高斯濾波、保邊濾波等。
為什麽要用保邊的濾波演算法

左圖使用的是高斯濾波,權重符合二維高斯分布,中間權重高,越往外權重越低,在各個方向上距中心同一距離的位置上的權重是一致的。這樣的摺積核簡單粗暴,不管影像顏色資訊如何,統一對待,所以在輸出影像上可見山石邊緣也變得非常模糊。
右圖使用的是雙邊濾波,摺積核在高斯核的基礎上增加了顏色差異的權重。對於顏色差異大的鄰近點,它的權重變小,對中心點的平滑影響減弱,邊緣可以被有效地保留下來。
人臉上有眉毛、眼睛、嘴等與皮膚顏色差異很大的區域,而且立體的五官上也會有明暗變化。這些邊緣如果使用高斯濾波會模糊成一團。但是使用保邊濾波,可以清晰地保留下五官和明暗區域,防止變平、失真。
讓我們來看一下雙邊濾波和高斯濾波套用在真實人像上的效果對比(點選圖片可檢視大圖):


套用高斯濾波演算法(sigma=4.0),可以觀察到人物臉部變得朦朦朧朧,眼鏡邊緣、鼻子邊緣和嘴部邊緣都變得不清晰了。

而套用雙邊濾波演算法(spaceSigma=4.0,colorSigma=18),可以觀察到人物五官基本上仍然是清晰,眼鏡邊緣也沒有什麽變化。
可見在對人像磨皮的演算法選擇上,使用雙邊濾波更為合理。
雙邊濾波演算法
雙邊濾波的原理
雙邊濾波演算法由C. Tomasi和R. Manduchi在1998年提出,論文名稱是Bilateral Filtering for Gray and Color Images。
雙邊濾波組合了空間上鄰近程度的權重和像素顏色值相似程度的權重。公式如下:
h(x)=k^{-1}(x)\int_{-\infty}^\infty\int_{-\infty}^\infty{f(\xi)c(\xi,x)s(f(\xi),f(x))d\xi}
k(x)=\int_{-\infty}^\infty\int_{-\infty}^\infty{c(\xi,x)s(f(\xi),f(x))d\xi}
c(\xi,x)=e^{-\frac{1}{2}\left(\frac{d(\xi,x)}{\sigma_d}\right)^2}, where, d(\xi,x)=d(\xi-x)=||\xi-x|| s(\xi,x)=e^{-\frac{1}{2}\left(\frac{\delta(f(\xi),f(x))}{\sigma_r}\right)^2}, where, \delta(\phi, f)=\delta(\phi-f)=||\phi-f||
其中,f是原始影像,h是濾波後影像,x是摺積核中心點, \xi 是x的相鄰點。摺積核包括了兩部份:空間權重 c(\xi, x) 衡量幾何空間上的鄰近程度(Geometric C loseness),顏色權重 s(f(\xi),f(x)) 衡量色彩空間上的相似程度(Photometric S imilarity)。
權重c和權重s都遵循高斯分布:離中心點的幾何距離越遠,權重c越小;和中心點的顏色差異越大,權重s越小。

上圖從左到右依次為:輸入影像(含有明顯的顏色變化邊界);空間摺積核c;顏色摺積核s;疊加了空間摺積核和顏色摺積核的完整摺積核c x s;濾波後的影像(保留了顏色邊界)
雙邊濾波的參數和效果
讓我們對比一下高斯濾波和雙邊濾波的效果。這兩種濾波器在OpenCV中都有實作,所以直接呼叫OpenCV的介面得到如下結果(點選圖片可檢視大圖):
註:實驗圖片使用經典的lena影像,512x512像素,tiff格式。

對比上面幾幅影像,可以看到雙邊濾波可以明顯地去處原圖上的噪點,並且保留了相對清晰的物體輪廓。對比原圖和spaceSigma=4,colorSigma=32的雙邊濾波結果,人物臉上和肩膀上的斑點都消失了,皮膚看起來光滑水潤。隨著參數改變,我們看到濾波結果發生了很大變化。
由於spaceSigma和colorSigma都是摺積核的變異數。某一部份的變異數變大,鐘形曲線變得平緩,各個權重的差異變小,說明不強調這一部份的影響。
spaceSigma值越小,畫面越清晰,值越大,畫面越模糊,大到極限時,變為值域濾波(閾值化)。
colorSigma值越小,邊緣越清晰,值越大,邊緣越模糊,大到極限時,變為高斯濾波。
如果spaceSigma相對於colorSigma變小,說明摺積核更強調距離中心點近的點。比如colorSigma=32,spaceSigma由16變為4時,可以看到顏色接近的區域內部變得沒那麽模糊了。
如果colorSigma相對於spaceSigma變小,說明摺積核更強調與中心點顏色接近的點。比如spaceSigma=16,colorSigma由128變為32時,可以看到邊緣沒那麽模糊了。
註1:
使用OpenCV時,如果不指定摺積核的尺寸,按照3通道 sigma\times6+1 計算。因此計算此組圖片時,當spaceSigma=4時,摺積核尺寸為25x25;當spaceSigma=16時,摺積核尺寸為97x97。
註2:
PSNR(Peak Signal to Noise Ratio),是一種最普遍,最廣泛使用的評價影像的客觀標準,單位是dB,其數值越大,失真越少。
雙邊濾波的缺點
雙邊濾波的摺積核是非線性的,因此計算復雜度高。不同位置的摺積核不同,不能預先計算或者執行FFT,計算起來比較費時。因此很多前輩做出了很多嘗試,提出了一些最佳化方法可以近似雙邊濾波的效果。
雙邊濾波的實作和最佳化
0. 基本實作
最基本的實作方式就是按照上文中的公式,對每個像素進行二維摺積計算。這裏使用OpenCV實作基本的雙邊濾波演算法,以RGB3通道為例:
void BilateralBlur(const Mat &srcImage, Mat &dstImage, int kernelSize, double sigmaColor, double sigmaSpace) {
int height = srcImage.rows;
int width = srcImage.cols;
int channel = srcImage.channels();
if (dstImage.rows == 0 || dstImage.cols == 0)
dstImage = Mat::zeros(srcImage.size(), srcImage.type());
double ct = -0.5 / (sigmaColor * sigmaColor);
double st = -0.5 / (sigmaSpace * sigmaSpace);
int radius = (kernelSize - 1) / 2;
double w;
double sw;
double cw;
for (int row = 0; row < height; ++row) {
for (int col = 0; col < width; ++col) {
double sumr = 0, sumg = 0, sumb = 0, sumw = 0;
Vec3b bgr0 = srcImage.at<Vec3b>(row, col);
for (int n = -radius; n <= radius; n += step) {
int y = clamp(row + n, 0, height - 1);
for (int m = -radius; m <= radius; m += step) {
int x = clamp(col + m, 0, width - 1);
Vec3b bgr = srcImage.at<Vec3b>(y, x);
sw = exp((m * m + n * n) * st);
double c = abs(bgr0[0] - bgr[0]) + abs(bgr0[1] - bgr[1]) + abs(bgr0[2] - bgr[2]); // sum of difference of each channel
cw = exp(c * c * ct);
double w = sw * cw;
sumb += b * w;
sumg += g * w;
sumr += r * w;
sumw += w;
}
}
dstImage.at<Vec3b>(row, col) = Vec3b(saturate_cast<uchar>(sumb / sumw),
saturate_cast<uchar>(sumg / sumw),
saturate_cast<uchar>(sumr / sumw));
}
}
1. 使用尋找表減少計算
在計算高斯函數的時候,因為含有指數運算,運算量比較大。同時,自變量部份都是整數,所以可以預先計算好權重尋找表,在摺積時直接找到對應的權重值。權重表計算如下:
vector<double> CalculateBilateralBlurColorWeights(int channel, double sigma)
{
vector<double> weights(256 * channel, 0);
double t = -0.5 / (sigma * sigma);
for (int i = 0; i < 256 * channel; ++i)
weights[i] = exp(i * i * t);
return weights;
}
vector<double> CalculateBilateralBlurSpaceWeights(int kernelSize, double sigma)
{
vector<double> kernel(kernelSize * kernelSize, 0);
int radius = (kernelSize - 1) / 2;
double t = -0.5 / (sigma * sigma);
int k = 0;
for (int i = -radius; i <= radius; ++i)
for (int j = -radius; j <= radius; ++j)
kernel[k++] = exp((i * i + j * j) * t);
return kernel;
}
2. 使用可分離的摺積近似計算
對於摺積核可以分解成一個行向量乘以一個列向量的形式時,例如:
\left( \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix} \right) = \left( \begin{matrix} a_h & b_h & c_h \end{matrix} \right) * \left( \begin{matrix} a_v \\ b_v \\ c_h \end{matrix} \right)
就可以把一次二維摺積分解成兩次一維摺積,單個像素摺積操作的計算復雜度從 O(N^2) 下降為O(N)。對於較大的摺積核而言,最佳化振幅是相當可觀的。實作時需要先對整幅影像做一次一維摺積,把摺積結果保存到臨時影像上,再對臨時影像做第二次一維摺積。
對於雙邊濾波的權重s部份,雖然分離後的結果不完全一樣,但是誤差不大,可以以這種方法做近似計算。
3. 使用遞迴方法近似計算
R. Deriche在1993年提出了一種遞迴高斯濾波方法,論文名稱是Recursively implementating the Gaussian and its derivatives。在這種方法中,二維高斯摺積核被分解成兩個一維高斯摺積核相乘,每一次摺積計算包含6次乘法和6次加法,與摺積核的尺寸無關。計算復雜度下降為O(1)。對於大小超過7x7的摺積核,效能都可以有所提升,摺積核越大提升越明顯。
受到這篇論文的啟發,很多學者都在探索如何遷移這種方法到雙邊濾波演算法中。比如Q. Yang在2012年提出了遞迴雙邊濾波方法,論文名稱是Recursive Bilateral Filtering。
本實驗使用了https:// github.com/ufoym/recurs ive-bf 提供的程式碼。
以下是上述最佳化方法的結果對比(點選圖片可檢視大圖):

實驗參數均為spaceSigma=4,colorSigma=32。
從PSNR數值來看,幾種最佳化方法和標準演算法區別不大。肉眼觀察,可見一些細微的差異,但整體效果接近。
4. 使用SIMD指令集
在CPU上,還可以使用SIMD指令集做進一步的加速,加速比例一般可以做到接近於數據並列數目。一般來說,比如在64位元寬的寄存器上使用8x8位元數據進行運算,加速比可以達到6-8倍。受限於篇幅,本文不進行詳細討論。可以參考https:// github.com/Fig1024/OP_R BF 提供的程式碼。
參考文獻
延展閱讀:











