直接上結論第一個人存活概率就是最高的。
題目是經典約瑟夫環問題的概率版本。
對於概率遊戲直接暴力模擬就好,如果沒有好的結果,那一定是模擬次數太少了,增加模擬次數即可。
另外,類似約瑟夫環的問題,基本可以用遞推公式求解。
兩種理解方式
不過看了一下評論區,看起來對開槍的概率有兩種理解。
1) 死亡概率不是定值
只有裝填子彈的的那個人,才會旋轉手槍旋轉輪。也就是剛填子彈時,開槍是1/6死亡率,如果沒有射出子彈,下一個人開槍,就會有1/5的概率射出子彈,然後1/4, 1/3,1/2, 1/1。
2) 死亡概率是定值
每次開槍都是1/6死亡率,也就是每個人在射擊前,都隨機旋轉一下手槍旋轉輪。
當然不管是哪種理解方式,都是第1個存活概率最高。
死亡概率不是定值時理論計算
采用遞推方式求解這個問題。
狀態定義
記 P(n, m, k) 表示 當遊戲有 n 個人且第1個人開槍射出子彈的概率為 \frac{1}{k} 時,第 m 個人的最終存活概率。
遞迴關係
於是可以找它的遞推公式,並不會復雜,按第一個人開槍後是否射出子彈分兩種情況就好。
1) 如果第一個人打出子彈,第2個人直接死亡,那麽人數就變為 n-1 , 而且槍會到第3個人手中並且概率會重設為 \frac{1}{6} 。於是相當於從第3個人開始對每個人重新標號繼續進行遊戲,所以原來的第1個人變為 n-1 人,第 m 個人變為 m-2 人。
2)如果第一個人沒打出子彈,那麽槍到2號手中,而且2號開槍射出子彈的概率增加為 \frac{1}{k - 1} 。於是相當於從第2個人開始對每個人重新標號繼續進行遊戲,所以原來的第1個人變為第 n 人,第 m 個人變為 m-1 人。
根據兩種情況得到如下遞推公式:
P(n, 1, k) = \frac{1}{k}P(n - 1, n - 1, 6) + (1 - \frac{1}{k})P(n, n, k - 1)\\ P(n, 2, k) = (1 - \frac{1}{k})P(n, 1, k - 1)\\ P(n, 3, k) = \frac{1}{k}P(n - 1, 1, 6) + (1 - \frac{1}{k})P(n, 2, k - 1)\\ \vdots\\ P(n, m, k) = \frac{1}{k}P(n - 1, m - 2, 6) + (1 - \frac{1}{k})P(n, m - 1, k - 1)\\ \vdots\\ P(n, n, k) = \frac{1}{k}P(n - 1, n - 2, 6) + (1 - \frac{1}{k})P(n, n - 1, k - 1)
其實就2號的遞推比較特殊,他可能第一槍就死掉。
邊界條件
邊界條件 P(1, 1, k) = 1 這是顯然的,只有一個人時,他總不會自殺吧。
目標
求解的目標是 P(n, i, 6) 對每個 1\leq i \leq n 。
然後實作就簡單記憶化搜尋了,關鍵程式碼如下:
from
functools
import
lru_cache
@lru_cache
(
maxsize
=
None
)
def
P
(
n
,
m
,
k
):
if
n
==
1
and
m
==
1
:
return
1.0
if
m
>
n
or
m
<=
0
:
return
0.0
if
m
==
1
:
prob_shoot
=
(
1.0
/
k
)
*
P
(
n
-
1
,
n
-
1
,
6
)
prob_not_shoot
=
(
1.0
-
1.0
/
k
)
*
P
(
n
,
n
,
k
-
1
)
if
k
>
1
else
0.0
return
prob_shoot
+
prob_not_shoot
else
:
prob_shoot
=
(
1.0
/
k
)
*
P
(
n
-
1
,
m
-
2
,
6
)
prob_not_shoot
=
(
1.0
-
1.0
/
k
)
*
P
(
n
,
m
-
1
,
k
-
1
)
if
k
>
1
else
0.0
return
prob_shoot
+
prob_not_shoot
def
compute_probabilities
(
n
,
k
=
6
):
probabilities
=
{}
for
m
in
range
(
1
,
n
+
1
):
probabilities
[
m
]
=
P
(
n
,
m
,
k
)
return
probabilities
具體結果如圖1所示,顯然第1個人的存活概率最大,不過跟第100個人差別不大。然後比較有意思的就是1到7的存活概率遞減,第8個人出現一個小峰值,其余的人存活概率整體趨勢上升。
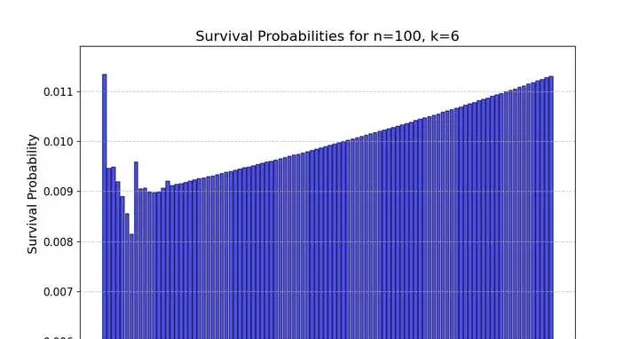
死亡概率不是定值時模擬實驗
進行1200萬模式實驗得到的存活概率和理論值對比結果如圖2,會發現幾乎重, 因此理論計算沒有什麽問題。
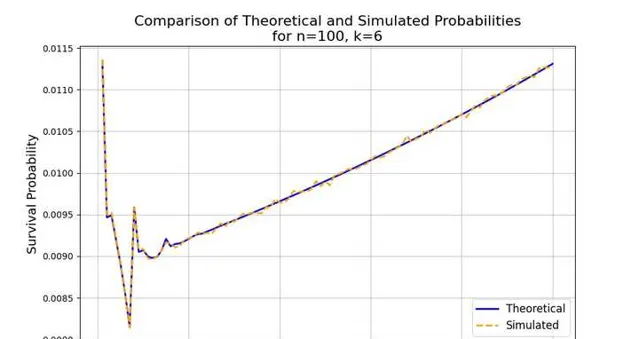
死亡概率不是定值時關鍵程式碼
import
random
#死亡概率不是定值
def
simulate_game
(
total_people
,
simulations
):
survival_counts
=
[
0
]
*
total_people
for
i
in
range
(
simulations
):
people
=
list
(
range
(
1
,
total_people
+
1
))
m
=
6
while
len
(
people
)
>
1
:
shooter
=
people
.
pop
(
0
)
if
random
.
randint
(
1
,
m
)
==
1
:
people
.
pop
(
0
)
m
=
6
else
:
m
-=
1
people
.
append
(
shooter
)
if
people
:
survival_counts
[
people
[
0
]
-
1
]
+=
1
return
survival_counts
具體1200萬次模擬實驗數據如下:
[136348, 113994, 114275, 110564, 107032, 102645, 97681, 115055, 108950, 109036, 107689, 107479, 108013, 108768, 109982, 109844, 109259, 109428, 110391, 110588, 110787, 111405, 111206, 111356, 111210, 111993, 112712, 112253, 113064, 112961, 113604, 114108, 114071, 114312, 114214, 114176, 115046, 115038, 116230, 115751, 115741, 116309, 117383, 117267, 117312, 117263, 117736, 118797, 118066, 118777, 118223, 119616, 119856, 120148, 120555, 120513, 120643, 121042, 121264, 121861, 122409, 122210, 122385, 122925, 123308, 123654, 124216, 125325, 124400, 124942, 125103, 126217, 125747, 126337, 126902, 127028, 127287, 127764, 127839, 128510, 127983, 128841, 129748, 129415, 130387, 130922, 131171, 131123, 131585, 132309, 132694, 132661, 133449, 133725, 134008, 133762, 135055, 135226, 135142, 135396]
死亡概率是定值時模擬實驗
這種理解的理論推導和實驗評論區都有,這裏就不重復推導了,就讓電腦做一下模擬實驗,做一個補充。進行1200萬次模擬實驗,得到的結果如圖3所示。
存活次數最多的是第1個人129708次,存活次數最少的3個是第2個人108017次
所以結論是
第1個人的存活率是最高的,但是和第100個人,第99個人沒有顯著的差別。
第2個人的存活旅明顯低於其他人,然後就是2到100的存活概率基本在增加。
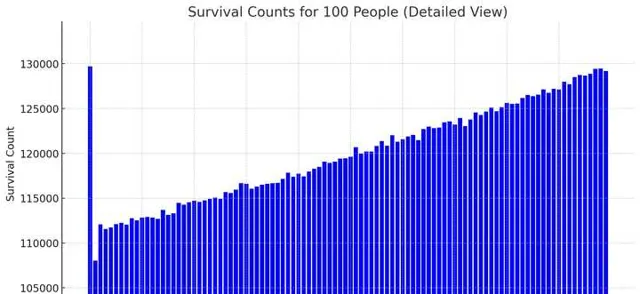
死亡概率是定值的關鍵程式碼
import
random
#死亡概率是定值
def
simulate_game
(
total_people
,
simulations
):
survival_counts
=
[
0
]
*
total_people
for
i
in
range
(
simulations
):
people
=
list
(
range
(
1
,
total_people
+
1
))
while
len
(
people
)
>
1
:
shooter
=
people
.
pop
(
0
)
if
random
.
randint
(
1
,
6
)
==
1
:
people
.
pop
(
0
)
people
.
append
(
shooter
)
if
people
:
survival_counts
[
people
[
0
]
-
1
]
+=
1
return
survival_counts
模擬1200萬次的實驗具體數據如下:
[129708, 108017, 112087, 111569, 111733, 112116, 112248, 112045, 112753, 112508, 112820, 112887, 112844, 112704, 113683, 113131, 113312, 114477, 114278, 114560, 114712, 114587, 114743, 114939, 115076, 114925, 115664, 115581, 115969, 116664, 116613, 116047, 116279, 116505, 116596, 116663, 116693, 117143, 117824, 117382, 117731, 117441, 117980, 118277, 118489, 119072, 118928, 119057, 119404, 119448, 119614, 120669, 119956, 120201, 120205, 120834, 121370, 120872, 122029, 121318, 121566, 121880, 122052, 121477, 122694, 122983, 122823, 122889, 123463, 123570, 123240, 123929, 123049, 123782, 124559, 124293, 124655, 125094, 124705, 125139, 125623, 125533, 125566, 126189, 126513, 126378, 126567, 127151, 126756, 127195, 127134, 127992, 127712, 128501, 128756, 128681, 128875, 129422, 129454, 129180]
最後
如果有幸玩這種遊戲,可以先寫遺書準備後事。
然後盡量讓自己是第一個開槍,如果不能,那就最後一個開槍。










