我來主要談一談 微分拓撲學 在數理經濟學中的套用。
德布魯教授在諾貝爾經濟學獎的獲獎演說中,提到過大數學家S.Smale(斯梅爾,沒錯就是非線性泛函分析中著名的Palais.Smale條件的斯梅爾,著名的微分拓撲學家,主要研究動力系統)向他介紹過一個重要的定理——Sard定理及其拓展:橫截-稠密性定理。橫截性的抽象定義如下:
橫截-稠密性定理:假設 Z\subset N 為 s 維光滑流形,稱對映 f:M\rightarrow N 橫截於 Z ,指下式成立:
df(x)(T_{x}M)\oplus T_{f(x)}Z=T_{f(x)}N 。
很多人可能光看定義頭都大了(其實這個定義有很直觀的幾何意義)。在這裏我不想過多地去談所謂橫截性的抽象定義, 我直接轉譯成初等微積分的語言 ,相信都能看懂:
假設有 M 個(非線性的)方程式, N 個未知數,組成的方程式組:
f^{1}(v_{1},v_{2}...v_{N};q_{1},q_{2}...q_{S})=0\\ ......\\ f^{M}(v_{1},v_{2}...v_{N};q_{1},q_{2}...q_{S})=0
或者縮寫成 f(v;q)=0 ,其中 q 是 S 個參數。 橫截-稠密性定理說的是 :
如果當 f(v;q)=0 時, M\times (N+S) 維矩陣的秩 rank Df(v;q) 為 M (行滿秩的),那麽對於 幾乎(按Lebesgue測度)所有的 q ,當給定這個 q 之後(比如 q=\bar{q} ), M\times N 矩陣 D_{v}f(v;q) 的秩也為 M 。
這跟經濟學有什麽關系呢?在進行大範圍分析的時候,我們總是把經濟的初始稟賦 w 作為參數。我們需要證明,對於幾乎所有的初始稟賦,經濟都是正則的!(經濟正則的重要意義後面會講述)
給定經濟體中第 i 個人對第 h 種商品的 超額需求函數:
z_{h}^{i}(p,w)=x_{i}^{h}(p,pw^{i}-w_{h}^{i}) ,那麽第 h 種商品的 總超額需求函數 為 :
Z_{h}(p,w)=\sum_{i=1}^{n}x_{h}^{i}(p,pw^{i}-w_{h}^{i})
從而 整個經濟體 的 總超額需求函數 為 C^{1} 對映 Z=[Z_{1}...Z_{h}...Z_{L-1}] 。根據我前面說的橫截性定理,我們可以證明對於幾乎所有的初始稟賦 w ,經濟都是 正則 的。
由於價格球體的正象限部份是緊的,因此,根據反函數定理,任何正則經濟都有有限個均衡點,使得超額需求 z(p)=0 ,即市場出清。
正則經濟之所以重要,一個關鍵點是在於我們可以進行指數分析,所謂指數,直觀理解,我們首先從一維開始:
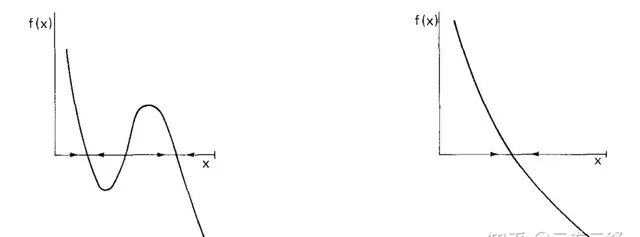
當價格(橫座標)很小的時候,超額需求(縱座標)為正,當價格很高時,超額需求(縱座標)為負。這是非常一般的假設,也非常符合常識。也就是說, 超額需求是指向區間內的(這個邊界條件非常重要!!!!!!!!) 。問題是我們如何透過這一最最普遍的假設入手,分析市場動力學的定性行為呢?
對於 高維空間的指數,也有非常直觀的畫面演示, 可以參考我的另一篇回答:
(Poincare-Hopf定理) 設N 是一個n 維緊致 帶邊光滑流形 ,f 為其上的光滑向量場,具有有限個零點。若對於\forall x\in\partial N ,有f(x)\cdot g(x) 為正(其中g(x) 為超曲面\partial N 的Gauss對映), 也就是說,要求向量場在流形邊界處指向外。 則該動態系統的指數和等於流形N 的歐拉示性數\chi(N) 。
我們剛剛說過,超額需求是指向區間內的。因此我們需要把向量場乘以負號(翻轉過來)以滿足定理的要求,因此就有:


註: 歐拉示性數\chi(D^{n}的正象限部份)=1 。(因為與 單點同倫! )。同時要使用Poincare-Hopf 定理,只有對正則經濟才有效,所以橫截-稠密性定理才那麽重要!











