看了很多回答,好像理解起來感覺還是 ......有點勉強,依然讓人覺得很「玄學」!我試試用一種初中物理水平就可以理解的方式聊聊這個問題。
本來零極點就是各種線性物理物件數學的抽象,不是簡單的特指某個元件,倒不如這樣說更準確,一個訊號經過一個零點或極點的作用後,會有什麽影響或變化!因為增加一個極點或一對極點(零點一樣),本質上就是傳遞函數上多乘了一個環節,也就是上一個環節出來的訊號,再經過這個環節大概會發生如何的變化。
先說一下極點,極點就兩種情況,一種是實數軸上的極點,一種是共軛極點,再復雜的線性系統都是由他們所組成的。先看單個實數軸上的極點,呃,增加了一個極點,這……不就是訊號又經過了一個慣性環節嗎?我們知道,一個階躍訊號經過一個慣性環節,經過3到4個 \tau (時間常數)差不多就進入穩態的訊號。我們先做個小實驗,如下圖。
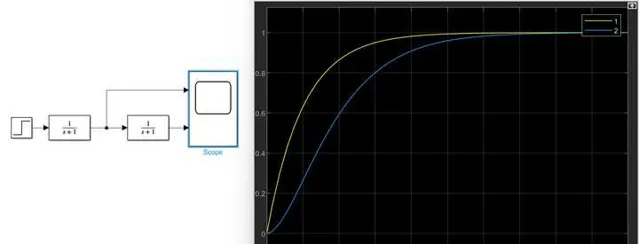
這個圖很簡單,關鍵怎麽去理解他。看黃色的曲線1,學自控的都懂,太熟悉了,一個階躍訊號經過一個慣性環節後本來陡峭突變的曲線變成了前面變化快,然後變化變慢的上升曲線,並且3到4個 \tau 的時間後就達到穩態。也就是說,一個激勵,或一個訊號,經過一個極點的環節之後,由於受到一階慣性的作用,他變緩了!用自控的語言說,上升率變慢了,上升時間和調節時間增加了。所以再看藍色曲線2,就是曲線1又經過了一個極點後的情況,所以他肯定更緩了!而且不可能會多出一個震蕩出來,畢竟階躍那麽劇烈的訊號經過慣性環節都沒引發震蕩。所以說每多一個負實數極點就是讓響應變緩,不管他在哪個負實數位置,位置只是影響變緩的程度。
那不同位置的極點(就是時間常數不同),影響的程度有多大呢?看下面的圖,時間常數分別是0.1,1,10的慣性環節(對應極點位置-10,-1,-0.1),階躍訊號經過這些環節的處理之後訊號變化的情況。

既然階躍訊號經過極點是這樣的效果,那其他訊號大家可以想象出來嗎?如果極點的位置離虛軸越近(就是時間常數越大,用ts+1=0,求極點位置),減緩的作用越強,反之減緩作用越弱。比如我們試試看用一個二階震蕩環節,分別經過時間常數不一樣的慣性環節,一個時間常數遠小於二階的時間常數,一個在同一個數量級,一個高於一個數量級的,看看效果如何?為了大家看得舒服,我直接把結果放出來,自己琢磨一下。
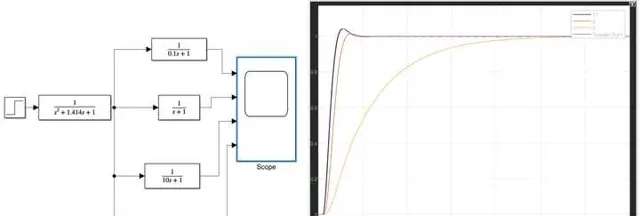
紫色的是典型的二階欠阻尼訊號,時間常數是1,可以看出來,經過時間常數是0.1的極點,響應曲線基本不變,經過同一級別時間常數的,響應變緩了,超調減少了,經過時間常數是他10倍的,那影響大了,連震蕩都緩沒了!所以我們的教材在二階系統的零極點影響那裏都會介紹,具有負實數極點動態特性的震蕩線減弱,上升時間和調節時間增長,超調減少,也就是慣性增強了。多了一個極點,就是多乘以一個慣性環節,慣性不增強了才怪!這,不就是簡單的線性思維的推論嗎?
如果這種說法對大家有幫助,有一點點贊或收藏,我再繼續說其他的影響。不過按照這種物理思維實驗的方式,應該對大家有了足夠啟發了。








