Meta-learning可以理解為一種求解問題的工具,下面舉一個例子,通俗的說明meta-learning的作用。在正常的machine learning中,需要將數據集分成trainset和testset,模型在trainset上進行訓練,在testset上評測效果。但是,在trainset上的訓練過程可能導致過擬合,進而引起在testset上效果較差。如何才能設計一種面向testset上效果的訓練方法呢?Meta-learning就能達到這個目的。Meta-learning直接評測在trainset訓練幾輪後的模型在testset上的效果,再使用這個效果作為訊號計算並回傳梯度,指導模型更新。Meta-learning的learn to learn,相比傳統的機器學習,進行了一個兩層的最佳化,第一層在trainset上訓練,第二層在testset上評測效果。
本文首先從不同角度介紹對meta-learning的理解,然後進一步介紹meta-learning的典型模型MAML的原理。在此基礎上,介紹了5篇近3年的頂會的論文,從3個角度揭示了meta-learning在學術界的最佳化方向。
1. Meta-learning的不同角度解釋
本小節從不同角度理解meta-learning,相關資料可以參考這篇meta-learning的survey,介紹的比較全面: Meta-Learning in Neural Networks: A Survey(2020) 。下圖給出了論文中對於meta-learning的詳細分類。
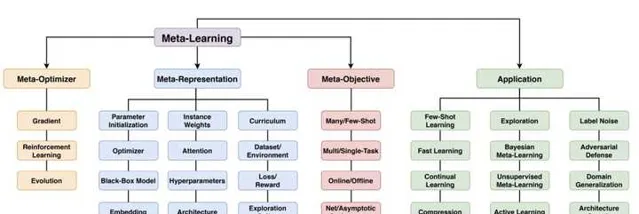
Meta-learning經常被理解為learn to learn,可以分為兩個階段:內迴圈和外迴圈。內迴圈階段,模型利用訓練樣本擬合某個特定任務;在外迴圈階段,對外迴圈的某個目標函數進行最佳化。內迴圈和外迴圈叠代交替進行。在上一節的例子中,在trainset上訓練就可以理解為內迴圈,而評估testset上的效果並以此為訊號更新網絡參數則可以理解為外迴圈。內迴圈的最佳化目標是trainset的效果,即模型的擬合能力,外迴圈的最佳化目標是testset的效果,即模型的泛化能力,也可以理解為外迴圈以泛化能力作為最佳化目標。對於meta-learning,從不同的視角也有不同的解釋,下面主要介紹從任務分布角度和兩層最佳化角度對於meta-learning的理解。
1.1 Task分布角度
從task分布視角理解,meta-learning的功能是利用多個task學習一個比較好的初始化參數,這個初始化參數在之前沒見過的task上finetune幾輪,能達到非常好的效果。為了達到這個目的,在學習階段,會有很多不同task的數據,比如貓狗分類、車船分類等等多個不同的任務,每個任務都被分為trainset和testset。在meta-learning的過程中,隨機采樣一些任務,首先透過內迴圈在這些任務的trainset上訓練,然後在外迴圈中,利用各個任務的testset評估模型效果,再用這個效果更新模型參數。整個過程在模擬訓練+finetune的過程,這樣得到的模型參數的意義,其實是「學習幾輪後,在當前任務上效果最好」的參數。
這個視角下的理解經常和多工聯合pretrain+finetune的思路形成對比。Pretrain-finetune的方法,首先用所有任務數據一起訓練模型,再在各個任務上finetune子模型,由於沒有meta-learning的最佳化目標,在pretrain階段關註的是所有任務整體效果最好,而不是finetune後每個任務的效果最好。而meta-learning是直接以finetune後效果最好為目標的。下面這個圖形象表達了meta-learning的學習過程,訓練階段找到的可能不是兩個任務最優點,而在finetune幾輪後能達到最優的點。

1.2 兩層最佳化視角
兩層最佳化視角指的是模型的最佳化目標包含兩層,例如上面提到的內迴圈和外迴圈,可以表示為如下的公式形式:
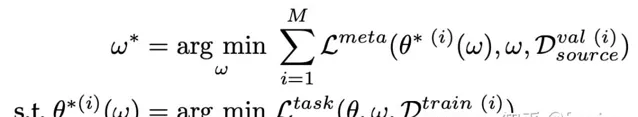
公式的第一行代表外層最佳化(外迴圈),第二行代表內層最佳化(內迴圈),兩層最佳化是依賴關系。內迴圈在trainset上以具體task為目標訓練得到一個中間參數,中間參數在外迴圈以外層最佳化目標在testset上訓練得到最終參數。
2 Meta-learning經典模型MAML原理
Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks(2017,MAML) 提出了MAML模型,也是目前最經典的meta-learning演算法之一,是很多後續meta-learning研究的基礎,理解MAML演算法原理是理解meta-learning的核心。首先我們明確MAML的目的,傳統的機器學習方法是在樣本維度進行學習,在單個任務的訓練集上訓練模型,希望模型在測試集上表現好。而MAML是在task維度進行學習,模型在訓練集可見的task上訓練模型,希望在未見過的task上效果好。為了達到這個目的,MAML在訓練過程中基於meta-learning思想,利用訓練集的task學習一個初始化參數,使這個參數在未見過的任務上finetune幾輪,就能達到較好的效果。
MAML的演算法流程如下圖,分為內迴圈和外迴圈兩個部份。首先采樣一部份task,將task劃分為trainset(support set)和testset(query set)。內迴圈階段,模型在這些task的support set上分別進行訓練,得到一個臨時的模型參數。外迴圈階段,模型使用這個臨時參數評估在每個task的query set上的效果,用這個效果去更新最初的模型參數。這個過程模擬了模型在一個任務上fintune幾輪效果能夠達到最優的過程,因此能夠實作我們最初的目標。
在MAML訓練完成後,如果想要套用於下遊任務中,需要在下遊任務的數據上finetune,以達到最優效果。總結起來,MAML可以分為兩個階段:meta-train(內迴圈+外迴圈叠代更新)、meta-test(在具體任務上finetune)。

3. Meta-learning近年最佳化方向
理解了MAML的核心思路後,我們重點介紹一下近幾年來,學術界對於MAML存在問題的進一步改進和最佳化,了解meta-learning最新研究方向。本文主要介紹數據增強、short-horizon bias、自適應超參數選擇三個方面。
3.1 數據增強
Meta-learning requires meta-augmentation(NeurIPS 2020) 指出,meta-learning存在兩方面的overfitting問題,分別為Memorization Overfitting和Learner Overfitting。其中Memorization Overfitting指的是,模型不需要用support set訓練,指根據query set的輸入就能準確預測出結果,這樣support set不起作用了,也就失去了meta-learning的意義。Learner Overfitting類似於傳統機器學習在trainset上的overfitting,指的是模型在meta-train階段的樣本上overfitting,在meta-test階段的新任務上效果不好。
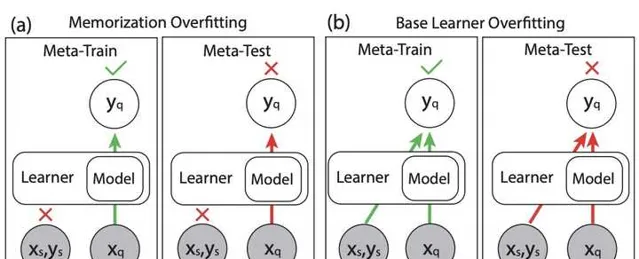
為了Memorization Overfitting,解決本文提出用CE-increasing進行數據增強,以此來讓模型必須透過學習support set才能把query set預測好。CE-increasing數據增強的核心是,對特征X和標簽Y進行變換後,一個特征X可能對應多個標簽Y,即根據X預測Y的條件熵增大。這相當於把一個任務變成多個任務(相同的輸入x,不同的輸出y),預測出query set必須要根據support set才能預測好,其本質上是在做task的數據增強。
Data Augmentation for Meta-Learning(ICML 2021) 探索了support set、query set、task、shot等4多個因素的增強對於meta-learning效果影響,並提出了meta max-up演算法,思路借鑒了max-up演算法,每次采樣task後,從多種數據增強方法中隨機生成新的樣本,選擇當前模型下loss最大的增強數據進行模型參數更新。
3.2 Short-horizon Bias
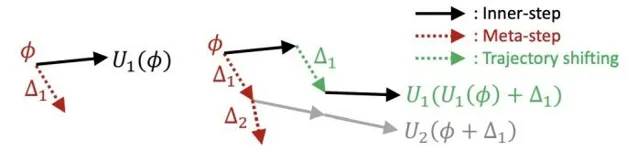
UNDERSTANDING SHORT-HORIZON BIAS IN STOCHASTIC META-OPTIMIZATION(ICLR 2018) 首先提出了meta-learning中存在的short-horizon bias問題。該問題指的是,內迴圈其實是在模擬模型finetune的過程,內迴圈輪數如果較小,對應的finetune輪數較小,這種情況下模型會出現貪心效應,finetune輪數小和finetune輪數大最終達到的最優點是不同的。只有當內迴圈輪數足夠大的時候,才能更真實模擬finetune過程,達到更好效果。然而,增大內迴圈輪數,意味著訓練時間大幅增加,因為多輪內迴圈後,才能進行一次外迴圈真正更新模型參數。
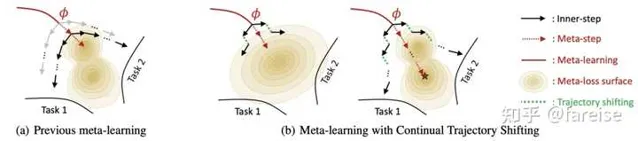
為了能夠增大內迴圈輪數,同時又能提升模型更新頻率, Large-Scale Meta-Learning with Continual Trajectory Shifting(ICML 2021) 提出了一種meta-learning新的最佳化方法。該方法每一次內迴圈,都伴隨著一次外迴圈,而不是原來的n次內迴圈對應一次外迴圈。該方法的核心如下圖左側更新方法和右側公式。在右側的公式中,約等號左側為正常的meta-learning第k個內迴圈後模型中間參數,在外迴圈進行更新得到的模型參數,可以近似等於右側。而右側的物理意義為,每輪內迴圈後,都外迴圈更新一次,並把模型初始參數進行一個和梯度相同的移動。該方法和傳統meta-learning的對比以及演算法細節如下圖。

3.3 自適應超參數
Meta-Learning with Adaptive Hyperparameters(NIPS 2020) 提出內迴圈中每個任務的學習率自適應的方法。原來的MAML在內迴圈更新參數時,學習率都是固定的,更好的應該是動態改變學習率、weight decay的,每個task在每個內迴圈step能夠自適應的更新。本文提出的方法為,在內迴圈的損失函數中給參數加一個l2正則,相當於約束當前task不能過擬合它的loss,推導梯度得到一個新的更新方法,如下面的公式。有a和b兩個參數確定,透過網絡自動學習這兩個參數。每個task每個step都有不同的a和b。a和b的生成函數采用一個NN網絡,輸入當前梯度和當前參數(反應當前的訓練狀態),輸出當前的a和b。生成a和b的NN網絡使用外迴圈更新。
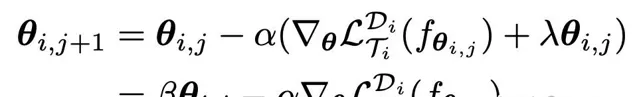
4. 總結
本文從基礎的meta-learning原理出發,從不同角度理解meta-learning,並進一步介紹了meta-learning中的代表性工作MAML。在此基礎上,介紹了5篇近3年來針對meta-learning進行最佳化的頂會論文。
如果覺得我的演算法分享對你有幫助,歡迎關註我的微信公眾號「 圓圓的演算法筆記 」,更多演算法筆記和世間萬物的學習記錄~









