對很多文科生來說,數學是十分困難的學科。我們經常會聽到有學生說,自己選文科是因為自己數學成績不好,不擅長計算,對數碼沒有感覺,所以只能選文科。
然而很少人知道,在西方很多大學裏, 數學系授予的其實是文學學士學位,數學也被認為是文科的一門。 數學為什麽會是文科?它可以被當成文科一樣學習嗎?
今天的文章就想和大家討論一下這個問題,同時希望大家不要再因為先入為主的文理分科觀念而害怕了數學。即使你是文科生,學習數學也能帶來很多好處。
為什麽數學是文科?
在我看來,大部份文科生害怕數學,或者不擅長數學,其原因不外是文理科截然二分的觀念深入人心。
事實上,當今教育體制裏的文理分科只有短短一百多年的歷史。相對之下,我們今天熟悉的基礎學科,比如數學、物理學、生物學、化學、歷史、文學等等,自誕生以來的兩千多年歷史裏,都是沒有明確分家的。古時的哲學家、思想家、學問家都不只精通一門學科。古希臘的教育就包括了文法、邏輯、修辭等等,與中國古時六藝兼備禮、樂、射、禦、書、數一樣,都是全人教育。
當今教育體制裏的文理分科在二十世紀形成。當時西方社會為了配合工業革命,把教育分成文科和理科,方便快速培育工業建設的人才,這種 分科完全是為了社會經濟的考量,不是學科的性質使然。
如果我們勉強要分文科和理科,它們的差別在哪裏?這個問題其實是不太好回答的,只可以勉強這樣講: 理科研究的是自然,文科研究的是人的精神活動。 物理現象、化學現象、乃至生理現象,都是發生在自然之中的,人類只能甪科學方法去理解和研究它;但歷史、政治、文學、藝術等等,是人精神活動的產物,如果沒有人,就不會存在這些領域。
根據這個文理科的定義,數學之所以是文科,因為數學也是人類精神活動的結果。這並不表示數學是人類主觀的創造,就如我們創作文學作品一樣;數學有它的客觀真理和規律,但它的客觀性只存在於人的理念之中,如果沒有人的精神活動,世界上沒有任何東西稱作「一」、「二」、「一加一等於二」。因此,數學研究的不是自然的規律,而是理念的規律。
如何用文科思維學習數學?
這個對數學的界定還是比較抽象,作為一個文科生,如果我就是對數碼不敏感,記不住公式,不理解數學,能怎麽辦?這個問題就牽涉到教授和學習數學的方法。

由於文理科的分科定型,學校都傾向於以理科的方法來教授數學,按研究物件分為代數、幾何學、統計、微積分等等,然後教授各種定理、公式和運算方法,最後是大量的解題練習。這種教學方法把數學塑造成了運算工具和解題遊戲。這種教學方式自然是對運算能力較高的學生有利的,但如果我天生對數碼不敏感,運算能力較低,是否就不適合學習數學呢?
事實上,運算能力、邏輯能力等等都是可以透過練習提高的,就好像我們能透過鍛練身體來提高體能一樣。因此如果你有意要提高自己做題解難的能力,只要努力做題,在錯誤中學習就可以了,沒有哪個人天生數學不好。不過這種機械式的操練仍然是把數學看成工具和遊戲。如何才是像文科一樣學習數學呢?如果我就是個「文科腦」,不想操練,是不是數學就學不好呢?
首先,所謂的「文科腦」通常指的是語言表達的能力。上面說過,文科是人類精神活動的成果,而 人類精神活動的成果,都可以在某種意義上被理解成語言和符號。 「文科式思維」就是利用語言和符號記錄精神活動的過程,例如我們用詩歌記錄情感、用畫筆記錄對風景的體會、用文字記錄歷史事件等等。如果這樣來理解,數學其實也只是一種語言,用來記錄和表達我們思維和推理的過程。

我們可以想想小時候是怎樣學習數碼的。我看到一個蘋果,爸媽說這是 1;然後他們又拿來另一個蘋果放在一起,說這是 2。我直接就能看到一個蘋果和另一個蘋果放在一起會有兩個蘋果。對小孩來說,1 和 2 只是兩個符號,用來記錄這個數蘋果的過程而已。當然,我們不能永遠用掰手指的方法來學數學,當我們能純熟運用符號的時候,就不需要具體的例子了。
不過,這個經驗仍然告訴我們, 再抽象的數學符號,其實都有相對應的例項和具體的思維過程。 如果把數學證明理解為表達的過程而不是運算的過程,我們就更容易獲得對數學的直覺了。
比如我們在做幾何學題目時,不妨可以思考整個圖形的構作過程。給定的長度、角度之所以能決定未知的長度、角度,是因為如果我們按照要求一步一步把圖形畫出來之後,未知的線段或角度就不能是任意的,它被給定的條件決定了。因此當我們重新構作圖式時,就會知道給定的參數如何一步一步規定未知的項。整個幾何學的證明,可以說是表達了我們構作這個圖的步驟而已。
其實很多數學上優美的定理和證明都不是生硬的運算結果。比如著名的七橋問題,說哥尼斯堡的公園裏有七座橋連線A, B, C, D四個區域,問有沒有方法不重覆地走遍七座橋而回到原點。
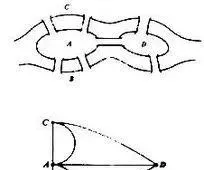
七橋問題圖示
解答的方法其實是很簡單的,數學家歐拉把每個區域理解成一個點,而橋是連線這些點的線。如果能不重覆地走遍所有點回到原點,那麽對於每一個點來說,如果要進去一次,就需要出來一次,於是所有點連線的線的數目都應該是偶數。但圖中點A有5條線、B、C、D各有3條線,都不是偶數,證明無法不重覆地走通。這整個證明沒有使用任何的運算,只需要我們把「過橋」這件事說清楚就可以了。
類似的思考方法也可以用在其他數學領域。只要你理解了數學家和科學家是如何利用數學作為一種語言來表達他們對世界的理解,以及解決具體的問題,數學就不只是抽象的運算,而是一個把事情「說清楚」的過程。
在數學系念本科的時候,對我影響最深的是一門必修的數學方法論課程。課程中教授還原了各種著名的定理在歷史中被發現、證明和修正的過程。從數學史的角度來看數學,就會知道數學怎麽一步一步發展到今天的樣子。你會看到人類的思維是如何與這些符號發生關系的。而且在課程中,教授要求我們用文字而不是公式來完成證明,這樣就強迫我們不能只停留在符號的遊戲上,而必須理解到符號背後代表的意義。理解了這些意義,才能自由地運用符號再現整個思考的過程。
用文科思維來學習數學,其意義就是在符號之外,進一步了解人類如何一步一步把事情「說清楚」的過程。

為什麽應該用「文科思維」看待數學?
用「文科思維」學習數學,更重要的不是大量的操練,而是嘗試去理解每一個定理背後的證明,以及證明背後的意義。其實這種學習方法才能掌握真正的數學精神,這種數學精神長久以來是西方精神文明的標桿。傳說柏拉圖學院的門外就樹了一個牌子,寫著「 不諳幾何者不得進內 」。

對古希臘人來說,數學不只是研究特定物件的一門學科,而是一切學科的典型。 一切學科的最高目標就是成為一門數學,或者幾何學。因此我們應該從數學學到的,不只是一些計算的技術,而是從中體會西方文明,乃至於現代科學文明的核心精神,理解「知識」,「學問」是如何誕生的。
數學有兩個特點一直支配著現代科學對知識和真理的理解: 純粹性 和 系統性 。
純粹性 的意思是,數學研究的理念,如數、形狀、關系等等,都完全是抽象的,不是任何現實物理世界的物件。正如,理念中的「圓」在現實世界中是不存在的;不論用什麽材質、有多精細的工藝,一個現實中圓的東西都不可能是絕對完美的,純粹的「圓」只存在於理念之中。古希臘數學的進步,使他們發現了在現實世界之上還有一個純粹的理念世界。柏拉圖認為,這個理念世界,或本體世界,比我們生活其中的世界更為真實和完美。現實世界只是對理念的模仿。正是由於理念世界的發現,早期的西方思想家意識到,大自然是可以理解的。世界並不是雜亂無章的,由不可知的神秘力量掌控;它背後有一個可以理解的規律,從此開始了對真理的追尋。
系統性 的意思是,對於一個領域的知識,其實都可以還原為一些基本的概念和公理。系統性科學的典型就是歐幾裏得的幾何學,【幾何原本】的重大意義在於,它用了五條簡單的公理,就能推理演繹出所有幾何學裏的定理和命題。這項成就使幾何學成為了幾乎所有學問的模範,我們現在接觸到的科學理論,幾乎都是模仿幾何學的方式建構的。無論任何學科,最開始都是一些基本的定義和假設,然後這些基本項就如磗塊一樣,相互構造成整個理論體系。

純粹性和系統性幾乎就是我們當今所學的任何一門學科的基本特征。哪怕是人文學科如歷史和文學,其實都離不開這種範式。 歷史表面上是對以前社會發生的事的記錄和還原,但歷史之復雜,以至於我們根本不能在重述歷史時不作出選取和解讀,在這個過程中,我們關心的就不再只是歷史事實,還有歷史背後的規律,還有歷史事件之間的邏輯關系。文學研究也不只是文學作品的體驗,它要求發掘文學作品背後體現出來的時代的人文精神,甚至要找到敘事的基本方式和規律。
不管是文科還是理科,只要它能稱得上一門學科,它的功能就在於使用簡單和精確的理念來把握復雜的現象,以至於發現現象之間的關系。 而對理念本身的純粹研究,就是數學。因此,如果你深入理解了一門數學,就能真正理解為什麽我們今天的各門學科會被建構成今天這個樣子,為什麽理念和系統性是一切知識體系的標準。這種理解對我們學習文科也有十分重要的作用。
數學中的想象與永恒
人文精神之所以動人,因為無論是文學,藝術,音樂,歷史,乃至宗教,都是一個個活生生的人,運用想象力來迎戰生命有限性的鬥爭故事。面對現實的不完美,我們寄托想象來創造一個完美的世界;面對有限而短暫的人生,我們希望用作品把精神永遠流傳。

在與命運鬥爭的歷史裏,人類總是脆弱的,但在數學裏,我們看到一絲希望。
數學能帶領我們的想象高飛。如果沒有了數學,人類大概不能想象遙遠的星空和地上的人間有著一樣的執行規律;大概不能想象時間流淌的速度可以改變;大概不能想象有物質沒有占有固定的空間位置。。。 我們總以為數學是理性和呆板的,文學是感性和想象的,但現代數學和科學帶給我們的想象空間,已經遠遠超越感性的想象力了。

而且,唯有在數學的領域,我們可以嚴格的談論
無限
和
永恒。
作為一個有限的生命,我們可能一生中看到的東西都是有限的,包括日月星辰,高山大海。永恒的造物主高不可攀,永遠不向世人現身。但在這個有限的人生裏,我們卻看到了永恒的數的理念和它們的規律。在數學中,古希臘哲學家第一次看到了無限的可能。這個無限是如何在有限的生命裏出現的?這個讓人驚嘆的問題,一直被視為西方形而上學的核心問題。雖然到現在我們都沒有一個明確的答案,但不可否認的是,
數學作為人文精神對永恒追求的實作,值得被所有追求人文價值的人所重視。
*長按關註 哲思時刻,哲學,人文,科普內容定期更新 *










