
上面出現的問題主要是機器不夠、記憶體不夠用。在深度學習訓練的時候,數據的batch size大小受到GPU記憶體限制,batch size大小會影響模型最終的準確性和訓練過程的效能。在GPU記憶體不變的情況下,模型越來越大,那麽這就意味著數據的batch size智能縮小,這個時候,梯度累積(Gradient Accumulation)可以作為一種簡單的解決方案來解決這個問題。
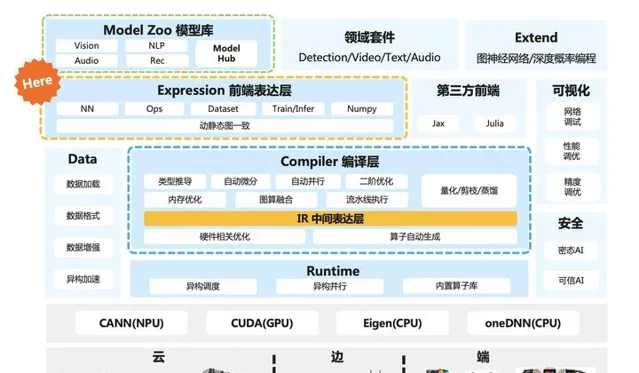
下面這個圖中橙色部份HERE就是梯度累積演算法在AI系統中的大致位置,一般在AI框架/AI系統的表達層,跟演算法結合比較緊密。
Batch size的作用
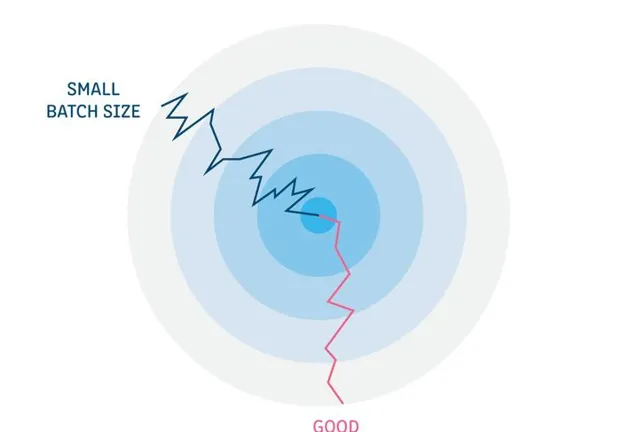
訓練數據的Batch size大小對訓練過程的收斂性,以及訓練模型的最終準確性具有關鍵影響。通常,每個神經網絡和數據集的Batch size大小都有一個最佳值或值範圍。
不同的神經網絡和不同的數據集可能有不同的最佳Batch size大小。選擇Batch size的時候主要考慮兩個問題:
泛化性 :大的Batch size可能陷入局部最小值。陷入局部最小值則意味著神經網絡將在訓練集之外的樣本上表現得很好,這個過程稱為泛化。因此,泛化性一般表示過度擬合。
收斂速度 :小的Batch size可能導致演算法學習收斂速度慢。網絡模型在每個Batch的更新將會確定下一次Batch的更新起點。每次Batch都會訓練數據集中,隨機抽取訓練樣本,因此所得到的梯度是基於部份數據雜訊的估計。在單次Batch中使用的樣本越少,梯度估計準確度越低。換句話說,較小的Batch size可能會使學習過程波動性更大,從本質上延長演算法收斂所需要的時間。
考慮到上面兩個主要的問題,所以在訓練之前需要選擇一個合適的Batch size。
Batch size對記憶體的影響
雖然傳統電腦在CPU上面可以存取大量RAM,還可以利用SSD進行二級緩存或者虛擬緩存機制。但是如GPU等AI加速芯片上的記憶體要少得多。這個時候訓練數據Batch size的大小對GPU的記憶體有很大影響。
為了進一步理解這一點,讓我們首先檢查訓練時候AI芯片記憶體中記憶體的內容:
因此,Batch size越大,意味著神經網絡訓練的時候所需要的樣本就越多,導致需要儲存在AI芯片記憶體變量激增。在許多情況下,沒有足夠的AI加速芯片記憶體,Batch size設定得太大,就會出現OOM報錯(Out Off Memor)。
使用大Batch size的方法
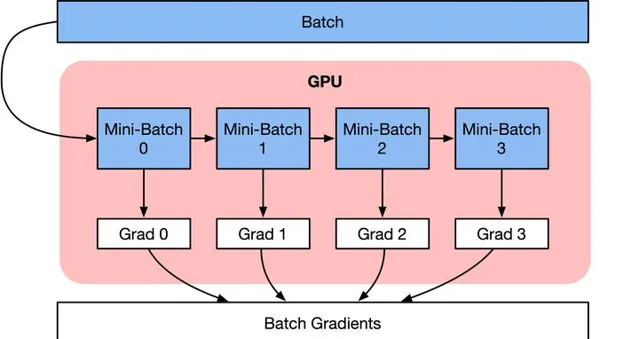
解決AI加速芯片記憶體限制,並執行大Batch size的一種方法是將數據Sample的Batch拆分為更小的Batch,叫做Mini-Batch。這些小Mini-Batch可以獨立執行,並且在網絡模型訓練的時候,對梯度進行平均或者求和。主要實作有兩種方式。
1) 數據並列 :使用多個AI加速芯片並列訓練所有Mini-Batch,每份數據都在單個AI加速芯片上。累積所有Mini-Batch的梯度,結果用於在每個Epoch結束時求和更新網絡參數。
2) 梯度累積 :按順序執行Mini-Batch,同時對梯度進行累積,累積的結果在最後一個Mini-Batch計算後求平均更新模型變量。
雖然兩種技術都挺像的,解決的問題都是記憶體無法執行更大的Batch size,但梯度累積可以使用單個AI加速芯片就可以完成啦,而數據並列則需要多塊AI加速芯片,所以手頭上只有一台12G二手卡的同學們趕緊把 梯度累積 用起來。
梯度累積原理
梯度累積是一種訓練神經網絡的數據Sample樣本按Batch拆分為幾個小Batch的方式,然後按順序計算。
在進一步討論梯度累積之前,我們來看看神經網絡的計算過程。
深度學習模型由許多相互連線的神經網絡單元所組成,在所有神經網絡層中,樣本數據會不斷向前傳播。在透過所有層後,網絡模型會輸出樣本的預測值,透過損失函數然後計算每個樣本的損失值(誤差)。神經網絡透過反向傳播,去計算損失值相對於模型參數的梯度。最後這些梯度資訊用於對網絡模型中的參數進行更新。
最佳化器用於對網絡模型模型權重參數更新的數學公式。以一個簡單隨機梯度下降(SGD)演算法為例。
假設Loss Function函數公式為:
Loss(\theta)=\frac{1}{2}\left(h(x^{k})-y^{k}\right)^{2}
在構建模型時,最佳化器用於計算最小化損失的演算法。這裏SGD演算法利用Loss函數來更新權重參數公式為:
\theta{i}=\theta_{i-1}-lr * grad_{i}
其中theta是網絡模型中的可訓練參數(權重或偏差),lr是學習率,grad是相對於網絡模型參數的損失。
梯度累積則是只計算神經網絡模型,但是並不及時更新網絡模型的參數,同時在計算的時候累積計算時候得到的梯度資訊,最後統一使用累積的梯度來對參數進行更新。
accumulated=\sum_{i=0}^{N} grad_{i}
在不更新模型變量的時候,實際上是把原來的數據Batch分成幾個小的Mini-Batch,每個step中使用的樣本實際上是更小的數據集。
在N個step內不更新變量,使所有Mini-Batch使用相同的模型變量來計算梯度,以確保計算出來得到相同的梯度和權重資訊,演算法上等價於使用原來沒有切分的Batch size大小一樣。即:
\theta{i}=\theta_{i-1}-lr * \sum_{i=0}^{N} grad_{i}
最終在上面步驟中累積梯度會產生與使用全域Batch size大小相同的梯度總和。
當然在實際工程當中,關於調參和演算法上有兩點需要註意的:
學習率 learning rate :一定條件下,Batch size越大訓練效果越好,梯度累積則模擬了batch size增大的效果,如果accumulation steps為4,則Batch size增大了4倍,根據ZOMI的經驗,使用梯度累積的時候需要把學習率適當放大。歸一化 Batch Norm :accumulation steps為4時進行Batch size模擬放大效果,和真實Batch size相比,數據的分布其實並不完全相同,4倍Batch size的BN計算出來的均值和變異數與實際數據均值和變異數不太相同,因此有些實作中會使用Group Norm來代替Batch Norm。
梯度累積實作
正常訓練一個batch的偽代碼:
for
i
,
(
images
,
labels
)
in
enumerate
(
train_data
):
# 1. forwared 前向計算
outputs
=
model
(
images
)
loss
=
criterion
(
outputs
,
labels
)
# 2. backward 反向傳播計算梯度
optimizer
.
zero_grad
()
loss
.
backward
()
optimizer
.
step
()
model(images)
輸入影像和標簽,前向計算。
criterion(outputs, labels)
透過前向計算得到預測值,計算損失函數。
ptimizer.zero_grad()
清空歷史的梯度資訊。
loss.backward()
進行反向傳播,計算當前batch的梯度。
optimizer.step()
根據反向傳播得到的梯度,更新網絡參數。
即在網絡中輸入一個batch的數據,就計算一次梯度,更新一次網絡。
使用梯度累加後:
# 梯度累加參數
accumulation_steps
=
4
for
i
,
(
images
,
labels
)
in
enumerate
(
train_data
):
# 1. forwared 前向計算
outputs
=
model
(
imgaes
)
loss
=
criterion
(
outputs
,
labels
)
# 2.1 loss regularization loss正則化
loss
+=
loss
/
accumulation_steps
# 2.2 backward propagation 反向傳播計算梯度
loss
.
backward
()
# 3. update parameters of net
if
((
i
+
1
)
%
accumulation
)
==
0
:
# optimizer the net
optimizer
.
step
()
optimizer
.
zero_grad
()
# reset grdient
model(images)
輸入影像和標簽,前向計算。
criterion(outputs, labels)
透過前向計算得到預測值,計算損失函數。
loss / accumulation_steps
loss每次更新,因此每次除以steps累積到原梯度上。
loss.backward()
進行反向傳播,計算當前batch的梯度。
optimizer.step()
梯度累加一定次數後,根據所累積的梯度更新網絡參數。
optimizer.zero_grad()
清空歷史梯度,為下一次梯度累加做準備。
梯度累積就是,每次獲取1個batch的數據,計算1次梯度,此時梯度不清空,不斷累積,累積一定次數後,根據累積的梯度更新網絡參數,然後清空所有梯度資訊,進行下一次迴圈。
參考文獻











