當我們在說「空間」的時候, 它真的「空」而能「間」物嗎? 或者說, 空間和物體有怎樣的區別? 一個獨特的觀點是, 二者是一致的. 當我們在觀察桌上的一個杯子時, 我們很自然的認為杯子「處在」這樣一個空間之中, 而沒有思考過, 實際上, 杯子自身也可以看作一個「空間」, 只是因為它的某些內容較低(比如維度), 使得我們不容易看出它的本質 —— 比如, 對於杯子上面的某個細菌而言, 這個杯子(的表面)完完全全可以看作一個能限制細菌運動的「空間」. 所以我們在說「空間」的時候, 到底是在說什麽? 有什麽 更一般的概念 蘊藏其中? 我們能否用 統一的語言 去描述空間和物?
下面, 我們拿 地球 做一個例子. 一個有趣的現象是, 即使在現今的教育體制下, 如果沒有刻意接受過這方面的知識, 那麽一個人很自然地會認為大地是平坦的: 這塊兒平坦的曲面上, 有房子、山脈、電線桿和人. 然而現在我們知道, 大地其實更像球面, 稱作地球.
為什麽看起來像一個平面? 因為它確實很大. 不過, 經過數千年的文明變革, 人們發現了如下證據:
- 古希臘人知道, 如果站在海邊的高巖上, 就會看到一條確定的 地平線 , 它並 不太遠 但是它外邊的船只都 看不見 了. 平坦的大地會很難解釋這個現象.
- 向著某一個方向一直走, 若走得足夠遠, 就會回到出發點地方. 這一點, 早在 15 世紀由 Columbus 和 Magellan 部份完成, 也就是著名的環球航行.
- 如果 沿著一條三角形路徑 旅行, 而這個三角形 足夠大 , 就會察覺出來, 這個 三角形的內角和 竟然大於 180^\circ. 假設你在行走的過程中, 路徑持續筆直, 處處無法察覺大地的彎曲, 那簡直就像一直走在一張平面上, 但每到達三角形的頂點就測量角度, 比如分別在北京、上海和廣州測量, 會發現內角和並不是 180 度, 這和平面幾何是矛盾的. 這仿佛是很有趣的「超自然現象」.
- 在距離「大地」 足夠遠的地方觀察 「大地」, 會發現它 置身於一個更龐大的黑色空間中 , 此時大地作為一顆球體而出現. 這一點, 於 20 世紀五十年代多地發射的衛星相繼完成. 首次「全身照」則於 1972 年由 NASA 完成.
你會發現, 在之後我們對流形的描述中, 會與上述現象較為相似.

同樣是千年來的統治, Euclid 的幾何體系一直被認為是描述宇宙的最好的幾何學. 這是很自然的. 然而這是不靠譜的, 和相信 2 維 Euclid 體系是描述大地表面最好的模型一樣不靠譜. 用 Lorentz 幾何學描述的時空模型現在被認為更好地描述了宇宙. 當然, 即使沒有狹義相對論, 天文觀測也並沒有給我們任何特殊的理由, 認為 Euclid 的幾何學「最好」. 我們甚至能大膽地類比, 有可能我們的 3 維空間是很大的 4 維球體的表面. 這會導致什麽有趣的現象? 類似在地球上走了很長的距離, 就發現「大地平面」的彎曲性質一樣, 沒準兒我們坐一趟火箭, 飛上足夠遠的距離且不改變航向, 最終會驚喜地回到原地. 令人惋惜的是, 暫時還沒有發現這方面的證據.
1. 微分流形
用數學來描述空間是輕松的, 但我們有必要將上述的概念做一些規範. 現在讓我們處在一個 3 維空間中, 只要給出某一座標系中的三元組 (x,y,z) 就能描述一個點的位置了. 構造一顆 3 維球體的 2 維球面 , 即
\{(x,y,z)\in\mathbb R^3|x^2+y^2+z^2=r^2\}.\\
我們說它是 3 維的球體, 因為上面的點都處在 \mathbb R^3 中, 但其實它的自由度只有兩個, 因此我們又認為它是 2 維曲面. 這就是所謂 外蘊 和 內蘊 的區別. 從外部的 環繞空間 來看, 地球是空間的一部份, 「維數」是 3; 而從內蘊的點與點間關系來看, 大地在局部角度上類似一張 2 維的平面, 「維數」是 2. 不同的角度指向了類似的事實, 即至少這個大地不是平坦的.
為什麽要做這樣的一個區分? 這實際上對應了之後提及的 流形 定義的不同角度. 內蘊的角度很重要, 因為有時候我們的條件會限制研究, 比如在噴射推進還沒有廣泛研究之前, 我們暫時看不到「外空間」, 只能從內蘊的角度判斷這個大地是平還是曲;亦或是 Klein 瓶,其內稟角度是完全有意義的曲面,但很難在 3 維空間中自然想象,當然,其實放到 4 維就自然許多了.實際上, 我們也不一定必須從外蘊角度去研究一個流形, 特別是當外蘊難以想象時.
比如說, 我現在說我們處在一個 3 維球面 之中, 因為普通的平直空間實在是不能描述我們的宇宙了, 假如已經有人發現飛船遠離之後又會回歸了. 身為科學家的你該怎麽研究? 我們可以嘗試著, 用 4 個座標去描述空間, 即 (x,y,z,w), 並加上條件
x^2+y^2+z^2+w^2=r^2.\\
這樣我們就把 3 維空間描述為了一個 4 維球體的表面. 這實在是難以想象, 我們的宇宙會有可能生活在一個更大的未曾觀測到的 4 維空間中. 但如果采取內蘊的方式定義, 那麽 3 維球面 S^3 將不再需要參照任何包含它的空間中.
讓我們又回到 2 維球面上. 想象一顆星球, 它可以是【星際穿越】裏的水球, 沒錯, 類似這樣一種被平靜的水面覆蓋的行星. 如果在北極丟了一塊大石頭進去, 那麽水波就會「擴散」, 不斷傳播, 類似一個半徑越來越大的圓. 這個圓任意時刻都是星球的緯圈, 海浪可以是像電影裏那麽大. 某個恰當的時候, 圈到達了赤道, 之後它竟然會開始「收縮」, 表面上的人覺得很突然. 最終水波到達南極.

類比到 3 維空間中呢? 註意我們現在在一個 3 維球面上, 如果某一點發出了光波, 波是一個不斷擴張的(2 維)球面. 讓我們始終處在球面的邊緣上觀察這顆球, 它擴充套件得很大很大, 一直到它伸展成一個平面了(而它的另一面處在我們看不見的無窮遠處). 現在它開始 裏外翻轉 , 從一個平面又逐漸收縮, 但收縮到另一個點上去. 這個「內外球皮翻轉」的過程並不求助於 4 維空間, 但我們已經觀察到, 這樣的現象不符合熟悉的 Euclid 空間了. 我們註意到了空間的彎曲 . 這種方法的威力在於, 我們可以真正對一個 3 維球面做了一個數學的 3 維描述, 而不是 4 維的.
(*程式碼*)
Export
[
"sphere.gif"
,
Table
[
Graphics3D
[{
Sphere
[{
1
/
a
-
Sign
[
a
]
/
(
10.125
),
0
,
0
},
Abs
[
1
/
a
]
-
1
/
(
10.125
)]},
PlotRange
->
{{
-1
,
1
},
{
-1
,
1
},
{
-1
,
1
}}],
{
a
,
-10.125
,
10.125
,
0.25
}]]
2 維和 3 維球面都是流形的基本例子, 在高階的數學課程中, 我們還會學到環面、射影平面等. 形象地說, 一個 d 維流形, 簡稱 d 流形 M, 就是這樣的幾何物件:
2. 圖
說回地球表面的問題,其內稟觀念就是用所謂的 圖冊 「2 維」地觀察曲面.「圖」的字眼其實是從地圖學和大地測繪學中借用的,其含義自明.處理流形的一個更一般的途徑就是用描述「局部」確切含義的圖冊.
一本世界地圖集, 一本真正生活意義中的圖冊書, 是由許多平面的地圖頁裝訂而成. 我們假設一張是中國地圖, 一張是俄羅斯地圖. 這兩張在繪制上顯然有重疊的地方, 我們有必要說明. 因為這兩個國家是緊挨的, 中間夾著蒙古, 它在兩頁地圖上都可以找到. 我們要說清楚蒙古在中國地圖的北部, 而在俄羅斯地圖的南部. 抽象就是, 這一頁的某點, 對應於另一頁的哪點 . 雖然一個圖冊畫的是 3 維宇宙中的一個物件, 但是地球表面的球面幾何卻只需從平面的圖頁上讀出. 這是自古以來的智慧 . 這件事做起來雖然不太方便, 但其實是可能的, 即我們甚至可以描述地球的旋轉, 比如它只需要讓第 27 頁的澳洲移動到 34 頁的某個位置, 此時圖冊的每一頁的圖都跟著變化了.
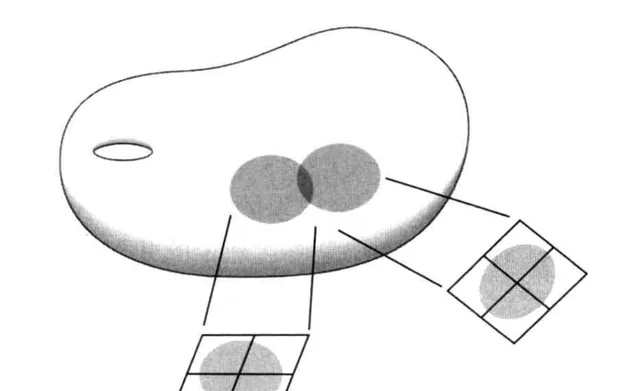
一個 2 維流形可以這樣用 2 維圖冊來定義. 一個 2 維球面可以這樣用數學描述: 這本圖冊只有兩頁, 每一頁都呈圓形. 一頁是北半球, 但是稍大一些, 越過赤道以便於南半球部份重疊; 一頁是南半球, 但也包含北半球鄰近赤道的一部份. 這兩頁地圖都是平坦的平面, 之上的島嶼可能會有些扭曲, 但我們也能說明出其扭曲程度.

圖冊的概念很容易推廣到 3 維情況. 只不過, 現在每一頁都變成了 3 維空間(的一部份). 我們說這樣的頁叫作 圖 , 也叫 座標卡 . 我們之前提到流形局部同胚於(對應維度)歐氏空間的一部份, 這就說明存在一個同胚對映 \phi 把流形上的點 x 一一對應地投到了歐氏空間中的 \phi(x), 同胚便讓這兩個點等同起來了, 就可以認為 \phi 是座標區圖. 這樣我們就可以利用 \phi(x) 的座標描述 x 了.
那麽, 上面的例子中, 就可以認為一張標準的中國地圖把地球表面上的中國部份的一個點與一個平坦的 2 維紙面上的點等同起來了, 成了一張標有經緯度的網格——經緯度自然是地圖上的座標系, 它可以對應轉換到地球上的座標系.此即是說,一個圖把流形一部份與其同維的歐氏空間之一部份等同起來.
一個 3 維圖冊就是若幹 3 維圖的集合, 當然也要指明, 一個圖的某部份對應於另一圖的哪些部份. 3 維球面有一個圖冊, 這個圖冊類似地包含了兩個立體的 3 維球體. 在一個球體靠近邊緣(球面)的部份的點與另一球體靠近其邊緣部份的點之間有一個對應. 我們所需的幾何學齊備了: 當你來到某個球體的邊緣附近時, 就會發現已經走到了重疊的區域, 而 平滑過渡 地, 同時走到了另一個球體裏去. 如果再往前走, 就一個球體而言, 你已經離開了它的地圖, 但是第二個球體將你接送了過去.
實際上, 圖冊本身就屬於流形. 我們將流形視作圖冊, 連帶著圖每個部份互相對應的規則. 在脫離特殊的情景外, 我們用圖和圖冊去定義流形是最方便的一般途徑.
Nash 定理指出, 可以認為所有的流形都是外蘊角度產生的, 即把一個 d 流形視作生活在更高維空間中的 d 維超表面. 但是要註意, 想總是找出一個簡單數學來定義這個超曲面不是個容易的事情. 但我們知道我們在描述流形, 是因為內蘊上, 每一點的小鄰域看起來都像 Euclid 空間. 也就是說, 無論哪種構造方式, 只有物件「局部同胚於 d 維 Euclid 空間」, 就可以認為構造了一個 d 流形.
微分流形的一個重要性質是可以對定義其上的函數做微積分. 積分要引入微碎形式的概念, 下面我們只考慮微分. 設 M 是一個流形, 和一個函數(也叫純量場) f:M\to\mathbf R, 要判斷 f 是否在 x\in M 可微, 首先要取 M 的一個包含 x 的圖, 並認為 f 是定義在該圖上的函數. 因為圖是 \mathbf R^d 的一部份, 其中我們本就可以做微分, 所以可微性是 f 具備的. 要使其可微性定義在流形上, 需要指出 f 屬於兩個重疊的鄰域(座標域)和圖(座標系), 並對兩個同時具備的圖可微. 交集處在兩個圖 \phi,\psi 下對映為 \mathbf R^d 的兩個(通常)不同的開集, 這兩個開集便也就等同起來了, 它們給出了不 同的座標 .這個關系就是 轉移 (遷移) 函數 , 或者叫 座標變換 , 比如可以是從 \phi 下的座標 x 變換到 \psi 中的 \psi(\phi^{-1}(x)). 自然, 遷移函數就是兩個圖之間的同胚.如果座標變換是可微的, 那麽同時可微性也就有保證了.
上述思想容易從實數值函數推廣到 f:M\to\mathbf R^n 上去, 甚至是 f:M\to M' 的對映. 然而, 判斷流形上的函數是否可微, 其實比求導要容易. 一個函數 f:\mathbf R^n\to \mathbf R^m 在 x 的導數是線性對映, 定義在流形上的函數也采取類似的方法. 不過註意的是, 該線性對映的定義域不是流形本身, 而是在 x 處的切空間. 隨後, 我們能一路構造微碎形式及其積分, 不過這些都是後話了.











