編輯:Aeneas 好困
【新智元導讀】 最近,陶哲軒向廣大網友和數學愛好者發起了挑戰:大眾數學愛好者、證明助理、自動化助手和AI聯合起來,是否可以證明擴充套件幾個數量級的數學問題?
想參加 陶哲軒 發起的「眾包」數學研究專案嗎?
機會來了!

AI輔助證明數學研究,越來越可行了
在傳統上,一個數學研究專案通常是由1到5名數學專家來完成的。
他們每個人都對專案的各方面都足夠熟悉,可以驗證彼此的貢獻。
但如果要組織起更大規模的數學研究專案,特別是涉及公眾貢獻的專案,就麻煩多了。
原因在於,很難驗證所有人的貢獻。
2023年底,陶哲軒宣布:將多項式Freiman-Ruzsa猜想的證明形式化的Lean4專案,在三周後取得了成功(圖為最新狀態)
要知道,在數學論證某個部份中的單個錯誤,可能就會使整個專案失敗。
而且,以一個典型數學專案的復雜程度來說,期待具有本科數學教育水平的公眾做出有意義的貢獻,也是不現實的。
由此我們也可以知道,把AI工具納入到數學研究專案中,也是極有挑戰性的。
因為AI會生成看似合理但實際上毫無意義的論證,因此需要額外驗證,才能將AI生成的部份添加到專案中。
好在,證明輔助語言(比如Lean)提供了潛在的方法,能夠克服這些障礙,並且讓專業數學家、廣大公眾和AI工具的合作成為可能。
這種方法的前提是,專案可以以模組化的方式分解成更小的部份,這些部份可以在不必理解整個專案的情況下就能完成。
目前的例子主要有將現有數學結果形式化的專案(比如對Marton最近證明的PFR猜想的形式化)。

這些形式化工作,主要是透過眾包方式由人類貢獻者(包括專業數學家和感興趣的公眾)完成的。
同時,還有一些新興的嘗試,試圖引入更多的自動化工具來完成,後者包括傳統的自動定理證明器,以及更現代的基於AI的工具。
探索全新數學問題,成為可能
並且,陶哲軒還認為,這種全新範式不僅可以用於形式化現有的數學,還可以用來探索全新的數學!
過去,他曾經和繼任組織過一個線上協作「Polymath」的專案,就是一個很好的例子。
不過,這個專案沒有將證明輔助語言納入工作流,貢獻就必須由人類主持人管理和驗證,這項工作非常耗時,也限制了將這些專案進一步擴大。
現在,陶哲軒希望,添加證明輔助語言能突破這個瓶頸。
而他尤其感興趣的,就是是否可能使用這些現代工具同時探索一類數學問題,而不是一次只關註一兩個問題。
本質上,這種方法是可模組化的重復任務,如果有適當的平台來嚴格協調所有貢獻,眾包和自動化工具可能會尤其有用。
如果用以前的方法,這種數學問題類別是無法擴大規模的。除非在多年時間裏,隨著個別論文慢慢地一次探索一個數據點,直到對這類問題獲得合理的直覺。
此外,如果有一個大型問題數據集,可能有助於對各種自動化工具進行效能評估,並且比較不同工作流程的效率。
這類專案最近的一個例子,是「忙碌河狸挑戰」。
在今年7月,第五個忙碌河狸數被證實為是47,176,870。

一些更早的眾包計算專案,比如「互聯網梅森質數大搜尋」(Great Internet Mersenne Prime Search, GIMPS),在內在精神上跟這些專案也有些類似,盡管它們使用的是更傳統的工作量證明機制,而不是證明輔助語言。

陶哲軒表示,很想知道是否還有其他現存的眾包專案探索數學空間的例子,以及是否有可用的經驗教訓。
陶哲軒提出新專案
為此,陶哲軒自己也提出了一個專案,來進一步測試這一範式。
這個專案受到去年MathOverflow問題的啟發。
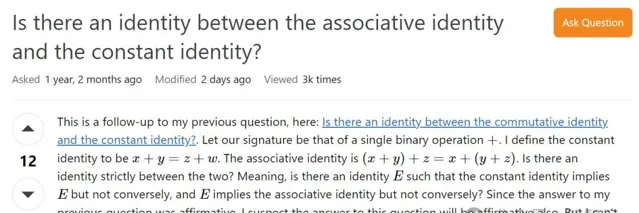
不久後,陶哲軒在自己的Mathstodon上,對它進行了進一步討論。

這個問題屬於泛代數(universal algebra)領域,涉及對原群(magma)的簡單等式理論的中等規模探索。
原群是一個配備了二元運算 的集合G。
最初,這個運算o沒有附加任何額外的公理,因此原群本身是較為簡單的結構。
當然,透過添加額外的公理,如恒等公理或結合律公理,我們可以得到更熟悉的數學物件,例如群、半群或 幺半群 。
在這裏,我們感興趣的是(無常數的)等式公理。這些公理涉及由運算o和G中的一個或多個未知變量構建的運算式的相等性。
此類公理的兩個熟悉的例子,是交換律x o y = y o x和結合律(x o y) o z = x o (y o z)。
其中x,y,z是原群G中的未知變量。
另一方面,(左)恒等公理e o x = x在這裏不被視為等式公理(equational axiom),因為它涉及一個常數e ∈ G。這類涉及常數的公理在本研究中不予討論。
接下來,為了闡明自己發起的研究專案,陶哲軒介紹了十一個關於原群的等式公理例子。
這些等式公理是僅涉及原群運算和未知變量的等式——

因此,舉例來說,等式7表示交換律公理,而等式10表示結合律公理。
常數公理等式1是最強的,因為它限制了原群G最多只能有一個元素;與之相反,自反公理等式11是最弱的,所有原群都滿足這一公理。
接下來,我們就可以探討這些公理之間的推導關系:哪些公理能推出哪些公理?
例如,等式1可以推匯出這個列表中的所有其他公理,而這些公理又可以推匯出等式11。
等式8作為特殊情況可以推匯出等式9,而等式9又作為特殊情況可以推匯出等式10。
這些公理之間完整的推導關系可以用以下哈斯圖(Hasse diagram)來描述:

這一結果特別回答了數學問答網站MathOverflow上的一個問題:是否存在介於常數公理(等式1)和結合律公理(等式10)之間的等式公理(equational axioms)。
值得註意的是,這裏大多數的蘊含關系都很容易證明。然而,其中存在一個非平凡的蘊含關系。
這個關系是在一個與前述問題密切相關的MathOverflow貼文回答中得到的:
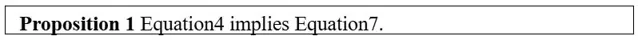
命題1:等式4蘊含等式7
證明:假設G滿足等式4,因此
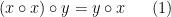
對所有x,y ∈ G成立。
特別是,當y = x o x時,可以得出(x o x) o (x o x) = (x o x) o x。
再次套用(1),可以得出x o x是 冪等 的:
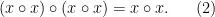
現在,在(1)中將x替換為x o x,然後使用(2),可以得出(x o x) o y = y o (x o x)。
尤其,x o x與y o y是可交換的:
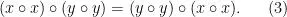
此外,透過兩次套用(1),可以得到(x o x) o (y o y) = (y o y) o x = x o y。
因此,(3)就可以簡化為x o y = y o x,這就是等式7。
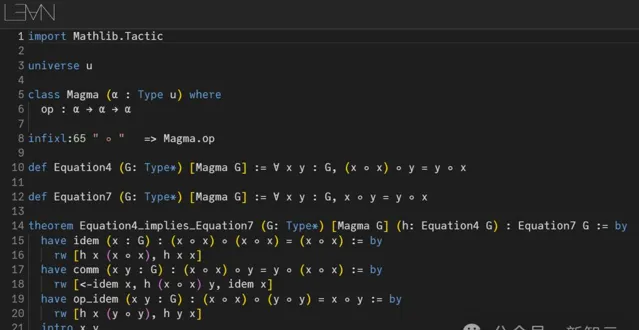
上述論證過程的形式化,可以在Lean中找到。
然而值得註意的是,確定一組等式公理是否決定另一組等式公理的一般問題,是不可判定的。
因此,這裏的情況有點類似於「忙碌河狸」挑戰,即在某個復雜點之後,我們必然會遇到不可判定的問題;但在達到這個閾值之前,我們仍有希望發現有趣的問題和現象。
上面的哈斯圖不僅斷言了列出的等式公理之間的蘊含關系,還斷言了公理之間的非蘊含關系。
例如,如圖所示,交換公理等式7並不蘊含等式4公理(x + x) + y = y + x。
要證明這一點,只需找出一個滿足交換公理等式7但不滿足等式4公理的原群的例子。
比如,在這種情況下,我們可以選擇自然數集N,其運算為x o y := x+y。
更一般地,該圖斷言以下非蘊含關系,這些關系(連同已指出的蘊含關系)完整描述了這十一個公理之間蘊含關系的 偏序集 :

在此,陶哲軒邀請讀者提出反例,來完成其中的部份證明。
最難找到的反例,就是等式9無法推出等式8了。
用Lean可以給出解決方案。
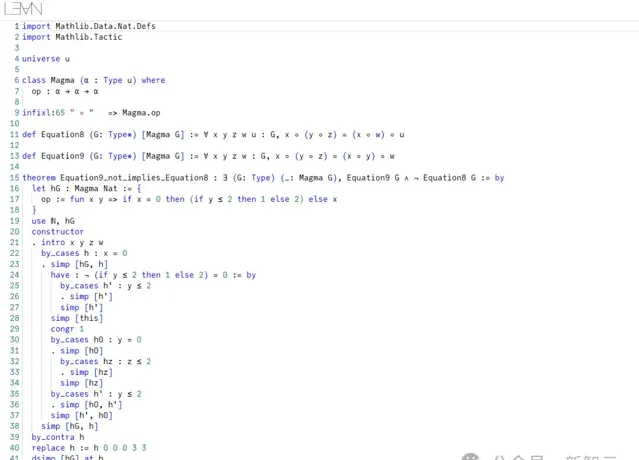
另外,陶哲軒還提供了一個GitHub儲存庫,包含了所有上述包含和反包含關系的Lean證明。
可以看出,僅僅計算11個等式的哈斯圖就已經有些繁瑣了。
而陶哲軒提出的專案,是嘗試將這個哈斯圖擴充套件幾個數量級,覆蓋更大範圍的等式集。
他提議的集合是ε,即最多使用原群運算o四次的等式集,直到重新標記和等式的 自反性 和對稱性公理。
這包括了上述十一個等式,但還有更多。
還有多少呢?
回想一下,卡特蘭數C_n是用二元運算o(套用於n+1個占位符變量)形成運算式的方法數;而給定m個占位符變量的字串,貝爾數B_m是為這些變量分配名稱的方法數(可以重新標記),其中允許某些占位符被分配相同的名稱。
因此,忽略對稱性,最多涉及四次運算的等式數量是
左側和右側相同的等式數量是
這些都等同於自反公理(等式11)。
剩下的9118個等式由於等式的對稱性成對出現,所以ε的總大小是
陶哲軒表示,自己還沒有生成這樣恒等式的完整列表,但他猜想,使用Python就可以輕松完成。
使用AI工具,應該能生成大部份所需的程式碼。
他表示,自己完全不清楚ε的幾何結構會是什麽樣子。
大多數等式會彼此不可比較嗎?它會分為「強」公理和「弱」公理嗎?
現在,陶哲軒的留言區,已經有了幾十條評論。
感興趣的讀者,陶哲軒也向你發出了邀請。











