金融的核心是數學嗎?
Quant這樣的職業最近幾年發展地很快,理性的數學方法無論如何確實是金融行業不可缺少的一部份,數學到底對於金融業以及從業者來說有多重要。
題主-知乎-推薦-過來-肯定答了-有-數學-就-有-我。
金融的核心是數學嗎?
題主-我-認為-是-吧-下面-我詳細-說。
列子---
Central Limit Theorem
We saw the DeMoivre-Laplace theorem for Binomial random variables, which essentially said that for large values of n, the standardization of the random variable Y \sim B(n, p), Z=\frac{Y-\mathbb{E}[Y]}{\sqrt{n \operatorname{Var}(Y)}} follows approximately a standard normal distribution. Since a binomial is a sum of i.i.d. zero/one random variables {X_i } ( counting the number of 」trials」 resulting in a 」success」 ), we can think of \frac{Y}{n} as the sample mean of X_1, . . . , X_n.
Therefore the DeMoivre-Laplace theorem is in fact also a result on the standardized mean of i.i.d. zero/one random variables. The Central Limit Theorem generalizes this to sample means of i.i.d. sequences from any other distribution with finite variance.
\text{Theorem} 1. ( Central Limit Theorem ) Suppose X_1, . . . , X_n. is a random sample of size n from a given distribution with mean \mu and variance \sigma^{2}<\infty. Then for any fixed number x,
\quad \lim _{n \rightarrow \infty} P\left(\sqrt{n} \frac{\bar{X}_{n}-\mu}{\sigma} \leq x\right)=\Phi(x)
We say that \sqrt{n} \bar{X}_{n} converges in distribution ( some people also say 」converges in law」 ) to a normal with mean \mu and variance \sigma^{2}, or in symbols:
\quad \sqrt{n}\left(\bar{X}_{n}-\mu\right) \stackrel{d}{\rightarrow} N\left(0, \sigma^{2}\right)
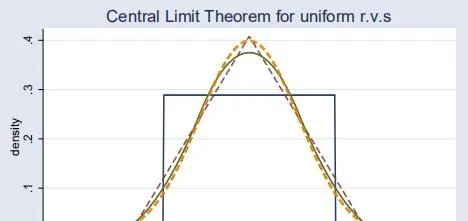
\text{Example} 1. Suppose X_1, . . . , X_n. are i.i.d. random variables where X_{i} \sim U[0,1] is uniform,
\quad f_{X}(x)= \begin{cases}1 & \text { if } 0 \leq x \leq 1 \\ 0 & \text { otherwise }\end{cases}
S_k = X_1 + X_2 + . . . + S_k
For k = 2, we get need to be careful about integration limits
\quad \begin{aligned} f_{S_{2}}\left(s_{2}\right) &=\int_{-\infty}^{\infty} f_{X}\left(s_{2}-w\right) f_{X}(w) d w=\int_{\max \left\{s_{2}-1,0\right\}}^{\min \left\{s_{2}, 1\right\}} 1 d w \\ &=\min \left\{s_{2}, 1\right\}-\max \left\{s_{2}-1,0\right\}= \begin{cases}s_{2} & \text { if } 0 \leq s_{2} \leq 1 \\ 2-s_{2} & \text { if } 1 \leq s_{2} \leq 2 \\ 0 & \text { otherwise }\end{cases} \end{aligned}
Now, the next calculations become more tedious because we always have to keep track of the integration limits and the kink points in the density. After some calculations, I get for k = 3
\quad f_{S_{3}}\left(s_{3}\right)=\int_{-\infty}^{\infty} f_{S_{2}}\left(s_{3}-w\right) f_{X}(w) d w= \begin{cases}\frac{s_{3}^{2}}{2} & \text { if } 0 \leq s_{3} \leq 1 \\ -\frac{3}{2}+3 s_{3}-s_{3}^{2} & \text { if } 1 \leq s_{3} \leq 2 \\ \frac{9}{2}-3 s_{3}+\frac{1}{2} s_{3}^{2} & \text { if } 2 \leq s_{3} \leq 3 \\ 0 & \text { otherwise }\end{cases}
By the rule on expectations of sums of random variables,
\quad \mathbb{E}\left[S_{k}\right]=k \mathbb{E}\left[X_{1}\right]=\frac{k}{2}
Also, since X_1, X_2, . . . , X_k are independent, we can use the rule on the variance of the sum
\quad \begin{aligned} \operatorname{Var}\left(S_{k}\right) &=\operatorname{Var}\left(X_{1}+X_{2}+\ldots+X_{k}\right)=\operatorname{Var}\left(X_{1}\right)+\operatorname{Var}\left(X_{2}\right)+\ldots+\operatorname{Var}\left(X_{k}\right) \\ &=k \operatorname{Var}\left(X_{1}\right)=k \int_{0}^{1}\left(t-\frac{1}{2}\right)^{2} d t=k\left(\frac{1}{3}-\frac{1}{2}+\frac{1}{4}\right)=\frac{k}{12} \end{aligned}
Therefore, the standardization Z_k of S_K is given by
\quad Z_{k}=\frac{S_{k}-\frac{k}{2}}{\sqrt{\frac{k}{12}}}
We can therefore calculate the densities of the standardizations Z_1,Z_2,Z_3 using the change of variables formula notice that the derivative is just equal to \sqrt{\frac{12}{k}}
\quad f_{Z_{1}}(z)= \begin{cases}\frac{1}{\sqrt{12}} & \text { if }-\sqrt{3} \leq z \leq \sqrt{3} \\ 0 & \text { otherwise }\end{cases}
\quad f_{Z_{2}}(z)= \begin{cases}\frac{1}{\sqrt{6}}+\frac{z}{6} & \text { if }-\sqrt{6} \leq z \leq 0 \\ \frac{1}{\sqrt{6}}-\frac{z}{6} & \text { if } 0 \leq z \leq \sqrt{6} \\ 0 & \text { otherwise }\end{cases}
\quad f_{Z_{3}}(z)= \begin{cases}\frac{1}{4}\left(\frac{3}{2}+\frac{z}{2}\right)^{2} & \text { if }-3 \leq z \leq-1 \\ \frac{3}{8}-\frac{z^{2}}{8} & \text { if }-1 \leq z \leq 1 \\ \frac{1}{2}\left(\frac{9}{8}-\frac{3}{4} z+\frac{z^{2}}{8}\right) & \text { if } 1 \leq z \leq 3 \\ 0 & \text { otherwise }\end{cases}
Now let’s check how this looks graphically: