文@ 小P家的021419
0 前言
在模型實際的業務落地過程中,大家是否遇到過這樣的場景:千辛萬苦訓練出了精度滿足業務需求的模型,終於可以上線啦!經過模型轉換、量化、打包等等一系列復雜的流程後,成功部署到實際硬件平台上,模型終於可以執行了!然而一波操作猛如虎,模型精度與當初訓練結果相比卻下降了不少……一臉茫然,不知所措,完全不知該從何下手,也不知道怎樣才能有效的恢復模型的訓練精度。 本次分享將針對部署流程中導致精度下降的頭號疑犯——模型量化進行分析,帶大家一探精度損失的幕後真相。
本文將從以下三個方面進行「揭秘」: - 量化的基本過程 - 量化的損失來源 - 常見芯片的量化支持
1 量化的基本過程
模型量化粗略地可以分為線上量化(Quantization Aware Training, QAT)和離線量化(Post Training Quantization, PTQ)兩大類。 雖然線上量化可以對量化後的模型精度提供更高的保障,但因其與模型的訓練過程過於耦合,開發成本和門檻較高,在模型部署階段采用更多的是另一種方式——離線量化。因此,本文主要針對采用離線量化方式對模型量化後,產生的精度損失進行分析。

神經網絡的量化本質上是將數據從連續空間 \mathbb{C} 對映到離散空間 \mathbb{D} ,這個過程通常包括三個階段: 數據縮放(scale),數據離散化(discretize),數據反向縮放(rescale) 。 三個階段之間關系的可以形式化描述如下:
Q(x) = f^{-1}(round(f(x)))
輸入數據 x 是來自連續空間 \mathbb{C} 的全精度值,即原始的浮點精度表示數據, Q(x) 是量化後在離散空間 \mathbb{D} 中的對應值,即定點類別的數據。 首先,縮放函數 f(\cdot) 將數據 x 從原始空間 \mathbb{C} 的表示範圍縮放到離散空間 \mathbb{D} 。 然後,縮放後所得到的數據被離散化為屬於離散空間 \mathbb{D} 內的中間值 z ,該階段最常用的離散函數是 round(\cdot) 。 最後,因為量化操作只改變數據的表示精度,不更改數據的表示範圍,所以離散化後的中間值 z 需要使用反向縮放函數 f^{-1}(\cdot) ,重新調整 z 到與 x 在原始空間 \mathbb{C} 中相同的表示範圍。在不同的量化方法中,數據縮放函數和數據離散函數各不相同。
當前較為成熟且使用較多的量化機制為線性均勻量化,指縮放函數 f(\cdot) 為線性對映函數,離散空間 \mathbb{D} 中的各個離散值之間的距離是均勻的。如使用的是線性量化,原始數據 x 的數值表示範圍為 [\alpha, \beta] ,縮放函數可以表示為:
f(x) = scale_{factor} * clip(x, \alpha, \beta) + zero_{point}
在對稱量化中, zero_{point} 設定為 0,同時要求 -\alpha = \beta ;在非對稱量化中,zero_{point} 會根據實際的數據範圍進行確定,通常會選取 zero_{point} = round(\frac{\alpha + \beta}{2}) 。
2 量化的損失來源
實際部署過程中,為了獲得更大的壓縮率和更快的執行速度,或受限於部署平台的計算單元類別,模型通常需要對整個網絡模型的權值和啟用值均進行定點量化。為了簡化討論,我們以一層摺積作為範例,采用線性均勻量化的方法,並假設 bias 已經透過最佳化融合到了 conv 的 weight 中。如下圖所示,整層網絡的計算誤差主要來自於三部份:
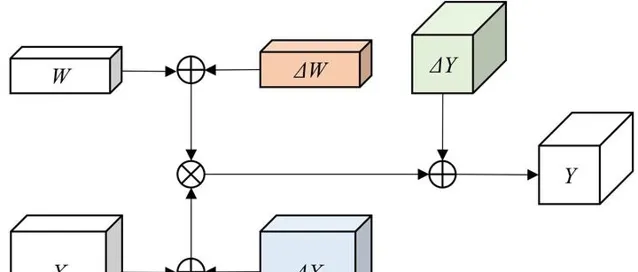
為了進一步考慮上述誤差是如何在計算過程中引入的,我們固定量化的位元位數 N 。根據量化的三個計算階段我們可以看到,均勻線性量化過程中涉及到的可能引入誤差的操作主要有三個: Round 操作,Clip 操作,scaling factor 的選取 。Round 和 Clip 操作引入的即為前文所指的各類取整和溢位誤差,不同的線性均勻量化方法和最佳化策略本質上即為不同 scaling factor 的選取。三者對誤差的引入和影響是緊耦合在一起的,互相作用和影響,需要進行一定的 trade-off。
Round 操作 實作數據的離散化,將原始連續空間的數值對映到距離它數值最近的離散點。原始數據 x 和其對映後所對應的離散值 x^{\prime} 之間的差值 \Delta x_r = x - x^{\prime} 即為 Round 操作引入的量化誤差。我們可以將誤差項近似看做服從均值為 0 的正態分布,則有:
\Delta x_r \sim U(-\frac{\beta_x - \alpha_x}{2^{N+1}}, \frac{\beta_x - \alpha_x}{2^{N+1}})
對於每一部份的量化誤差, 其最大值不會超過兩個相鄰的量化離散值的間距,根據公式可知離散量化值之間的間距由原始數據的動態表示範圍 \beta - \alpha 決定。在 N 固定的情況下,動態表示範圍越大,由 Round 操作引發的量化損失也就越大。
Clip 操作 對 [\alpha, \beta] 外的數據進行截取,使得所有的數據都在動態表示範圍內。這些超出範圍的數據 x 需要截取對映到 \alpha 或者 \beta , 之間的差值即為 Clip 操作引入的量化誤差。
\Delta x_c = \frac{1-sgn(x-\alpha)}{2}(\alpha-x) + \frac{1-sgn(\beta-x)}{2}(x-\beta)
我們來看一個服從正態分布的浮點數據進行線性均勻量化的過程示意:
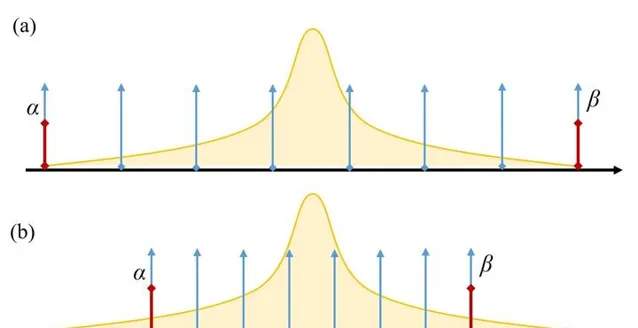
在圖3(a) 中,我們選取原始數據的真實最小值和最大值作為動態表示範圍 [\alpha, \beta] ,因此不存在超出範圍的數值點,即 \Delta x_c = 0 ;因動態表示範圍過大,各個離散數據值之間的距離較大,會導致 \Delta x_r 偏大。在圖3(b) 中,我們選取了較為合適的動態表示範圍來盡可能減小 \Delta x_r ,使得較多的數據分布在 [\alpha, \beta] 外圍,這些數據會引入較大的 \Delta x_c ,在長尾分布中引入的誤差尤為明顯。當前不同的量化演算法和最佳化策略往往是尋找一個恰當的 [\alpha, \beta] ,使得 \Delta x_r+\Delta x_c 較小。
Scaling factor 和動態表示範圍在不同的量化方法中有著不同的計算方法,例如線上性均勻量化中,二者之間的關系為:
scale_factor = \frac{2^N - 1}{\beta - \alpha}
通常確定了二者中的一個,另外一個可以根據公式計算得來。除了上述提到的 \Delta x_r 和 \Delta x_c , scaling facor 引入的量化誤差主要來源於各個離散數值利用率的平衡性。例如在圖3(a) 中,動態範圍選取較大帶來的另外一個弊端,即為離散數值利用率不均衡的問題。對於 N-bit 的量化,離散數值共有 2^N 種選擇(在部份量化策略中會強制保留 1-bit 表示數值 0,則離散數值的選擇剩余 2^N - 1 種)。神經網絡的原始浮點數據通常服從長尾正態分布,大部份的數值分布在均值附近,量化後對映到 0 值附近;小部份數值會分布在遠離均值的位置,帶有一定資訊量無法完全直接舍棄。較大的動態範圍使得離散數值之間的間距較大,大部份分布在均值附近的數據只能對映到少量的離散值上,導致 N-bits 的實際表示能力會損失 1 \sim 2 bits 甚至更多。 如何平衡各個離散數值之間的數據分布和利用率,是當前一些量化策略減少量化損失的方向。
3 常見芯片的量化支持
需要進行量化的模型,其部署目標平台多為邊緣側/終端側,即對模型的大小和執行速度有一定限制和要求的移動端和嵌入式器材。較為常用的典型硬件平台有 NVIDIA Jetson 系列 GPU、Qualcomm Hexagon 系列 DSP、以及新興的神經網絡加速器。在加速器系列中,我們選取寒武紀(Cambricon) 的推理芯片為例,各類硬件平台對量化的支持情況如下表所示:
| 硬件平台 | 後端推理庫 | 權值數據量化支持類別 | 是否支持外部參數寫入 |
|---|---|---|---|
| NVIDIA Jetson [1] | TensorRT | per-tensor & per-channel | Yes |
| Quanlcomm Hexagon DSP [2] | SNPE | per-tensor | No |
| Cambricon MLU [3] | CNRT | per-tensor & per-channel | Yes |
其中 per-tensor 的量化方法也稱 per-layer,指對於給定的網絡層的 weight tensor 中的所有數據共享一個量化參數;per-channel 也稱 per-axis,指對於給定網絡層的 weight tensor,每一個 axis 對應一個 channel,每個 channel 有自己獨立的量化參數。通常情況下,per-channel 因為量化的粒度更細致,量化參數的自由度更高,往往更優於 per-tensor 的量化精度。 NVIDIA TensorRT 在對權值(weights) 的量化上支持 per-tensor 和 per-channel 兩種方式,采用對稱最大值的方法[4];對於啟用值(activations) 只支持 per-tensor 的方式,采用 KL-divergence 的方法進行量化;量化參數既支持內部自動生成,也支持外部指定,支持 weights 和 activations 采用不同的指定方式。更為詳細的機制解析和使用方式已有官方技術文件[5]和很多文章[6]進行了分析講解,感興趣的同學可以自行閱讀,此處不再贅述。 Quanlcomm Hexagon DSP 的官方後端推理庫 SNPE 只支持 per-tensor 的量化方式,采用非對稱最大最小值的方法[7],並提供 Enhanced Quantization Mode 進行精度最佳化,暫不支持外部量化參數寫入。為了補償SNPE在使用時的量化精度損失,Quanlcomm 推出了自己的模型量化壓縮工具 AIMET[8],支持 DFQ[9]、AdaRound[10]等量化演算法,依托於 AIMET 也可以實作部份外部量化參數的寫入。透過對AIMET源碼的閱讀,我們也可以獲得如何把量化參數寫入SNPE後端的方法。寒武紀 MLU 系列加速器的官方後端為 CNRT,同樣支持 per-tensor 和 per-channel 兩種量化方法,也支持外部參數的寫入,但只支持 weights 和 activations 采用同樣的指定方式,即同時由內部生成或同時由外部指定。我們可以看到,當前的硬件平台除了自身的工具鏈提供的原生量化方法外,大部份均支持外部參數的寫入,透過指定 scaling_factor 或動態範圍 [\alpha, \beta] 二者之一,另外一個在內部透過計算得到。當原生量化工具無法滿足模型部署精度需求時,我們可以透過誤差分析,自行調整量化參數,從而達到恢復精度的目的。
4 結語
本文對量化過程中的誤差來源進行了粗略的歸類,理解這些誤差如何在計算過程中引入,並對各個誤差項之間的耦合和影響關系進行了分析。當前很多量化演算法和最佳化策略本質上還是在尋找一些減小這些誤差項的方法,並在其中尋找平衡點。例如,AdaRound 演算法不再采用四舍五入的方法,而是采用一種自使用的策略動態決定向上取整還是向下取整,從而減小 Round 操作引入的誤差項 \Delta x_r ;DFQ 演算法透過計算恒等性修改權值數據的分布,減少長尾部份的數據,從而減少Clip操作引入的誤差項 \Delta x_c ,同時也可以有效降低 \Delta x_r 和離散值利用率低的問題;ACIQ[11] 演算法直接透過對最佳化問題求解,得到最優的動態範圍,從而降低上述誤差項,等等。本文對量化誤差背後的基本原理進行了介紹,關於如何評估哪類誤差對整個網絡最終的結果起到了更大的影響,如何根據損失去選擇合適的量化演算法等問題,歡迎持續關註 AI 框架技術分享模型部署專題系列。
PS:歡迎大家關註 AI 框架技術分享專欄內容,如果有感興趣的技術內容和難點歡迎隨時指出,可以多多評論留言。我們也希望能透過本次技術分享讓大家了解到更多的 AI 框架前沿技術,也期待和大家一起探討,更歡迎大家加入我們,一同為 AI 框架及 AI 發展貢獻力量!簡歷直投郵箱:[email protected]
參考文獻
[1] NV TensorRT官方文件 https:// docs.nvidia.com/deeplea rning/tensorrt/developer-guide/index.html
[2] SNPE官方文件 https:// developer.qualcomm.com/ docs/snpe/model_conversion.html
[3] 寒武紀MLU290使用者手冊 https:// usermanual.wiki/Cambric on-Technologies/MLU290
[4] NV 2017-05-06 Presentation Slices https://www. slideshare.net/cfregly/ advanced-spark-and-tensorflow-meetup-20170506-reduced-precision-fp16-int8-inference-on-convolutional-neural-networks-with-tensorrt-and-nvidia-pascal-from-chris-gottbrath-nvidia
[5] 8-bit-inference-with-tensorrt Slices https:// on-demand.gputechconf.com /gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf
[6] Int8量化-介紹(一) https:// zhuanlan.zhihu.com/p/58 182172
[7] SNPE量化說明 https:// developer.qualcomm.com/ docs/snpe/quantized_models.html
[8] AIMET https:// github.com/quic/aimet
[9] Data-Free Quantization Through Weight Equalization and Bias Correction https:// arxiv.org/abs/1906.0472 1
[10] Up or Down? Adaptive Rounding for Post-Training Quantization https:// arxiv.org/abs/2004.1056 8
[11] Post-training 4-bit quantization of convolution networks for rapid-deployment https:// arxiv.org/abs/1810.0572 3










