是指經典的感知不確定性導致的規劃軌跡畫龍問題?
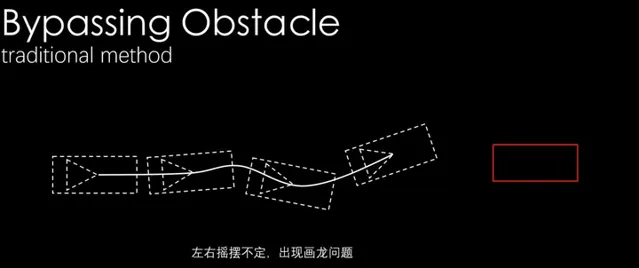
要解決這個問題可以看看 Contingency Planning 的相關內容。一種常用的方法是不只是規劃一條軌跡,而是規劃一個軌跡樹。
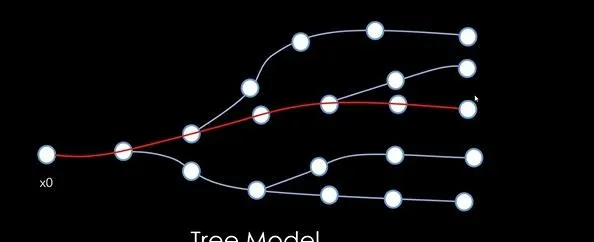
在軌跡樹的根部(共用的部份)資訊較少,此時規劃的軌跡會同時相容所有可能的決策。當資訊充足時,才進行決策(軌跡樹分叉),比如決定左轉還是右轉。這樣可以避免畫龍的問題。
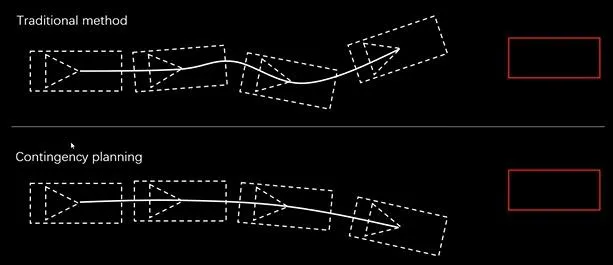
另外, A Non-Conservatively Defensive Strategy for Urban Autonomous Driving - 知乎 (zhihu.com) 中提供了一個十字路口讓行還是透過(yield or pass)的情境。從圖中可見此時同時規劃了pass和yield的兩條軌跡,當yield的概率越高(即pass的概率越低)時,共用部份的軌跡會越遷就yield,即便最後是pass,整體軌跡也是先減速後加速。這樣整個軌跡的加速度是保持平滑的,避免了在yield和pass之間切換導致的頻繁加減速。
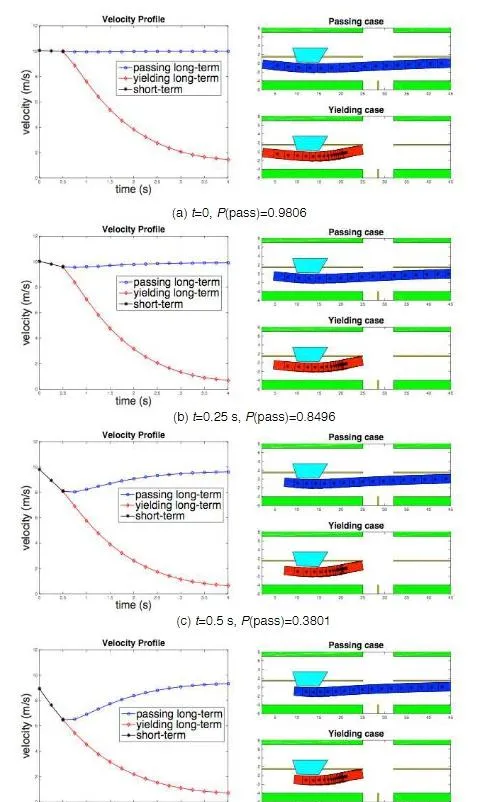
@論文推土機 大佬對這方面的文章做了很全面的總結,詳見這篇文章。
重點推薦一篇思路比較清晰,方便入門的經典論文Contingency Model Predictive Control (CMPC)。筆者最近有時間可能會嘗試復現一下。
另外,根據我自己的理解,這種方法背後的思想,其實是將決策和規劃兩個獨立的模組進行融合,使得最終結果能從 "模組最優"(局部最優) 變成 "系統最優"(全域最優)。從這種思想出發,一種自然的想法就是能否直接將決策規劃融合為一個整體的 "端到端" 問題,透過求解這個整體的決策規劃問題來得到最優的軌跡? @Invictus 金老師在這篇文章中分享了圖森在這方面的一些工作,不過沒有講具體的求解方法(所以大佬什麽時候出專著講講全域最佳化演算法orz)
文中圖片來源
其他參考資料推薦











