没想到是个科研人员提的问题,还问的这么具体,那我简单从严谨(瞎扯)的角度说一下。作为红警营长水平,经验还是不少的,还是有资格讲讲这个。
红警2坦克交战的唯象动力学:兰开斯特方程方法
一童天下*1
1物理系,b乎,地球,银河系
ABSTRACT
In this Letter, 我们用兰彻斯特战斗学理论讨论了红警中坦克队形与数量的影响,建立了描述部队战斗力的唯象理论。用这一方法可以简洁明了的解释为什么一字长蛇阵会出现奇怪的战损比。灰熊坦克和犀牛坦克实际的性价比is also investigated. 我们也给出了改善玩家红警坦克操作表现的建设性建议。It is anticipated that our results would constitute an indispensable component of nonequilibrium statistical physics for RedAlert2.
1*https://www. zhihu.com/people/yi-ton g-tian-xia-86-69
I,Introduction
红色警戒2是风靡全球的即时战略(RTS)游戏,与星际争霸,魔兽世界,帝国时代并称为RTS游戏四大名著。即使游戏已经发布超过20年,游戏的发行商westwood已经被收购,红色警戒2还是在中国有不小的热度。近年来,红警HBK08,红警魔鬼蓝天等b站up主的视频广受欢迎,前者充电量甚至一度冲击上b站第一。红色警戒2游戏视频的爆火吸引了很多新手玩家重温这款经典游戏。但是RTS游戏都有较高的门槛,很多玩家无法适应。这其中一个很fundamental的问题就是,为什么同样坦克数量交战,总有一方会输?
In this Letter,我们引入局部作战区域的概念。将整个坦克交战简化为若干局部交战在时间上的累计。这些局部交战的集合,就相当于是某种系综。为了讨论动力学,我们引入了 classical兰开斯特战斗学方程来唯象分析这类问题。Throughout this paper,我们主要考虑兰开斯特平方律成立的情况。
II,坦克队形的定量分析
很多人看到为什么双方坦克数量差不多,可以打出惊人的战损比时感觉不可思议(08视频弹幕,奇损现=奇怪的战损比出现了),这里面除去操作(点杀,残血后拉),坦克质量(你灰熊怎么可能打得过犀牛),血量(被辐射烫了一次什么的)这些区别,最大的决定性因素就是坦克的队形。
为什么队形这么重要呢?很多人不理解。实际上很简单,虽然坦克是个现代武器,但是在红警里面坦克的射程其实非常近(只有几个车身的距离),所以实际上两军交战的时候,处于作战状态的坦克数量是非常有限的。而真正决定此时谁会亏的,是这个 作战状态局部范围内的胜负 情况。所以结论就很明确了,一字长蛇阵中,比如下图红方。看似红蓝双方都是16个坦克,但是在交战区域绿色圈里面其实是8v4,显然蓝色赢。然后红色后面的坦克进场还是面临以少打多这样的状况。以此类推, 全程红色都是在以少敌多。 自然红色会输了
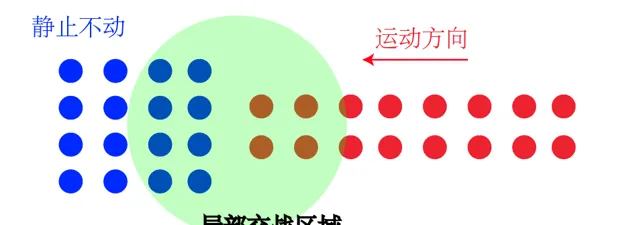
所以我们看到,真正决定胜负的其实并不是绝对的数量,而是每一个瞬间局部交战的情况。将这每一个瞬间局部交战的得失积分,看谁先消耗到0谁就输了。实际上操作的坦克的时候往往也会遇到不小心一下子一字长蛇了,之后还得调整过来,但是一开始还是要吃亏。
知道了这个原理,题目里面说「一字长蛇」是不好的队形,这就是不严谨了,不好也是看相对于谁不好
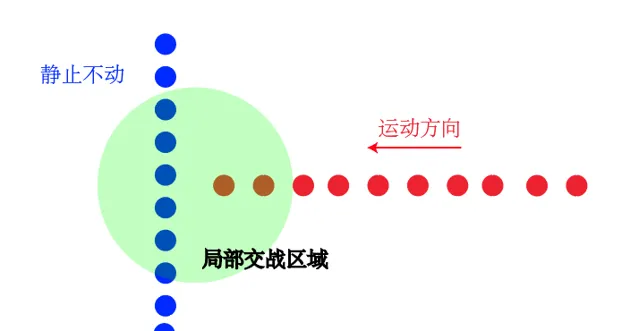
同样是一字长蛇阵,猜猜看哪一方会赢?
至于局部交战时候,到底数量的差异会有多大。我们用如下简单理论分析,假设双方坦克数量分别用 x(t) 和 y(t) 表示,我们很合理的假设一方坦克单位时间的减少量,应该是正比于对方坦克的数量的(敌人越多火力越猛,我们人也死的越多),就有
\frac{\mathrm d}{\mathrm d t}x(t)=-ay(t)
以及
\frac{\mathrm d}{\mathrm d t}y(t)=-bx(t)
这里 a,b 都是正的常数,可以用来代表 y,x 队伍的单个坦克的战斗力。
这个方程组我相信物理系学生都很熟悉,这种互为求导关系的方程在多自由度振动,电动力学等等很常见。为了方便读者我还是详细得写一下,易得
bx(t)\frac{\mathrm d}{\mathrm d t}x(t)-ay(t)\frac{\mathrm d}{\mathrm d t}y(t)=0
也就是
\frac{\mathrm d}{\mathrm d t}[bx^2(t)-ay^2(t)]=0
说明 bx^2(t)-ay^2(t) 是守恒量,那么有
bx^2(t)-ay^2(t)=bx^2(0)-ay^2(0)
其中 x(0),y(0) 代表初始时候的队伍数量。我们假设双方都是一样的坦克,那么 a=b ,初始的格局是4打5,看起来差别不大吧?带入 x(0)=4,y(0)=5,x(t_{\rm final})=0 进去,看看 x 队死光的时候 y 队还剩多少?结果发现
y(t_{\rm final})=3
没想到仅仅是多了一个坦克,居然结果是可以剩下来三个!这就是兰开斯特平方关系,其实战斗力是和队伍数量(在一定的假设下)的平方成正比的。所以数量差距会被平方一样的放大。在上面第一张图的例子中,8打4的情况下,可以剩下来 \sqrt{8^2-4^2}\sim6.9 大致七个,基本上也就没有损失。持续下去,当然就是「奇怪的战损比出现了」
红警是一个规则简单的游戏,上面的讨论适合于双方都是一样的坦克(比如都是0级犀牛),出场都是满血,没有带狗的情况。这是很常见可以满足的。
那如果是犀牛打灰熊呢?显然此时 a\neq b 。但是他们到底比值是多少?这也可以反向运用兰开斯特平方率求出,根据经验(参见操作水平相同的情况下,同等价格的犀牛坦克和灰熊坦克谁更厉害?),犀牛与灰熊战损交换比可以近似为 1:1.5 ,那么相当于是说 x(0)=1,y(0)=1.5,x(t_{\rm final})=0,y(t_{\rm final})=0 ,解得 b/a=2.25 ,也就是说从经验反推出犀牛的有效战斗力超过灰熊的两倍!要知道犀牛900,灰熊还要700(甚至加了工业工厂打折后犀牛只要675更加便宜),所以说灰熊是真正的垃圾兵种,性价比极低。
当然至于为什么灰熊这么差,这里有很多分析,我觉得比较合理的有,红警2的不平衡性有哪些? 。也可以看我的分析操作水平相同的情况下,同等价格的犀牛坦克和灰熊坦克谁更厉害?
III,队形优化分析
那么在游戏过程中,如何才能操控好队形呢?这里就不扯理论了,只说干货
1,交战前调整坦克聚集到一块,操作:框起来全部a一下地板(对动员兵这招尤其有效)
2,移动坦克的时候不要一下子点很远,要一点一点移动,红警2的寻路算法是有问题的,拖动很远很容易变成一字长蛇
3,不要过桥和别人打,不要硬冲狭窄路口
4,交战前把狗移动到坦克前方,逃跑时移动到坦克后方,抗伤害
5,移动坦克的时候尽量左右或者上下平移,斜着移动不容易保持队形
6,把1星,3星坦克移动到队伍中间,不要一上来就被别人点死了
IV,Summary
To conclude, 我们使用了兰开斯特战斗学方程分析红警2中坦克对战的关键因素,并给出了动力学方程。As a future prospect, 我们还需要讨论坦克升级,带狗,有动员兵,有地堡,有辐射工兵时候的坦克交战情况。并借助蒙特卡洛模拟,分子动力学模拟的技术讨论红警中的坦克交战问题。
Reference
本文不需要任何参考文献










