对很多文科生来说,数学是十分困难的学科。我们经常会听到有学生说,自己选文科是因为自己数学成绩不好,不擅长计算,对数字没有感觉,所以只能选文科。
然而很少人知道,在西方很多大学里, 数学系授予的其实是文学学士学位,数学也被认为是文科的一门。 数学为什么会是文科?它可以被当成文科一样学习吗?
今天的文章就想和大家讨论一下这个问题,同时希望大家不要再因为先入为主的文理分科观念而害怕了数学。即使你是文科生,学习数学也能带来很多好处。
为什么数学是文科?
在我看来,大部分文科生害怕数学,或者不擅长数学,其原因不外是文理科截然二分的观念深入人心。
事实上,当今教育体制里的文理分科只有短短一百多年的历史。相对之下,我们今天熟悉的基础学科,比如数学、物理学、生物学、化学、历史、文学等等,自诞生以来的两千多年历史里,都是没有明确分家的。古时的哲学家、思想家、学问家都不只精通一门学科。古希腊的教育就包括了文法、逻辑、修辞等等,与我国古时六艺兼备礼、乐、射、御、书、数一样,都是全人教育。
当今教育体制里的文理分科在二十世纪形成。当时西方社会为了配合工业革命,把教育分成文科和理科,方便快速培育工业建设的人才,这种 分科完全是为了社会经济的考量,不是学科的性质使然。
如果我们勉强要分文科和理科,它们的差别在哪里?这个问题其实是不太好回答的,只可以勉强这样讲: 理科研究的是自然,文科研究的是人的精神活动。 物理现象、化学现象、乃至生理现象,都是发生在自然之中的,人类只能甪科学方法去理解和研究它;但历史、政治、文学、艺术等等,是人精神活动的产物,如果没有人,就不会存在这些领域。
根据这个文理科的定义,数学之所以是文科,因为数学也是人类精神活动的结果。这并不表示数学是人类主观的创造,就如我们创作文学作品一样;数学有它的客观真理和规律,但它的客观性只存在于人的理念之中,如果没有人的精神活动,世界上没有任何东西称作「一」、「二」、「一加一等于二」。因此,数学研究的不是自然的规律,而是理念的规律。
如何用文科思维学习数学?
这个对数学的界定还是比较抽象,作为一个文科生,如果我就是对数字不敏感,记不住公式,不理解数学,能怎么办?这个问题就牵涉到教授和学习数学的方法。

由于文理科的分科定型,学校都倾向于以理科的方法来教授数学,按研究对象分为代数、几何学、统计、微积分等等,然后教授各种定理、公式和运算方法,最后是大量的解题练习。这种教学方法把数学塑造成了运算工具和解题游戏。这种教学方式自然是对运算能力较高的学生有利的,但如果我天生对数字不敏感,运算能力较低,是否就不适合学习数学呢?
事实上,运算能力、逻辑能力等等都是可以通过练习提高的,就好像我们能通过锻练身体来提高体能一样。因此如果你有意要提高自己做题解难的能力,只要努力做题,在错误中学习就可以了,没有哪个人天生数学不好。不过这种机械式的操练仍然是把数学看成工具和游戏。如何才是像文科一样学习数学呢?如果我就是个「文科脑」,不想操练,是不是数学就学不好呢?
首先,所谓的「文科脑」通常指的是语言表达的能力。上面说过,文科是人类精神活动的成果,而 人类精神活动的成果,都可以在某种意义上被理解成语言和符号。 「文科式思维」就是利用语言和符号记录精神活动的过程,例如我们用诗歌记录情感、用画笔记录对风景的体会、用文字记录历史事件等等。如果这样来理解,数学其实也只是一种语言,用来记录和表达我们思维和推理的过程。

我们可以想想小时候是怎样学习数字的。我看到一个苹果,爸妈说这是 1;然后他们又拿来另一个苹果放在一起,说这是 2。我直接就能看到一个苹果和另一个苹果放在一起会有两个苹果。对小孩来说,1 和 2 只是两个符号,用来记录这个数苹果的过程而已。当然,我们不能永远用掰手指的方法来学数学,当我们能纯熟运用符号的时候,就不需要具体的例子了。
不过,这个经验仍然告诉我们, 再抽象的数学符号,其实都有相对应的实例和具体的思维过程。 如果把数学证明理解为表达的过程而不是运算的过程,我们就更容易获得对数学的直觉了。
比如我们在做几何学题目时,不妨可以思考整个图形的构作过程。给定的长度、角度之所以能决定未知的长度、角度,是因为如果我们按照要求一步一步把图形画出来之后,未知的线段或角度就不能是任意的,它被给定的条件决定了。因此当我们重新构作图式时,就会知道给定的参数如何一步一步规定未知的项。整个几何学的证明,可以说是表达了我们构作这个图的步骤而已。
其实很多数学上优美的定理和证明都不是生硬的运算结果。比如著名的七桥问题,说哥尼斯堡的公园里有七座桥连接A, B, C, D四个区域,问有没有方法不重覆地走遍七座桥而回到原点。
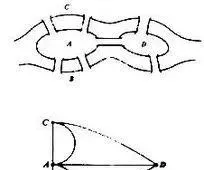
七桥问题图示
解答的方法其实是很简单的,数学家欧拉把每个区域理解成一个点,而桥是连接这些点的线。如果能不重覆地走遍所有点回到原点,那么对于每一个点来说,如果要进去一次,就需要出来一次,于是所有点连接的线的数目都应该是偶数。但图中点A有5条线、B、C、D各有3条线,都不是偶数,证明无法不重覆地走通。这整个证明没有使用任何的运算,只需要我们把「过桥」这件事说清楚就可以了。
类似的思考方法也可以用在其他数学领域。只要你理解了数学家和科学家是如何利用数学作为一种语言来表达他们对世界的理解,以及解决具体的问题,数学就不只是抽象的运算,而是一个把事情「说清楚」的过程。
在数学系念本科的时候,对我影响最深的是一门必修的数学方法论课程。课程中教授还原了各种著名的定理在历史中被发现、证明和修正的过程。从数学史的角度来看数学,就会知道数学怎么一步一步发展到今天的样子。你会看到人类的思维是如何与这些符号发生关系的。而且在课程中,教授要求我们用文字而不是公式来完成证明,这样就强迫我们不能只停留在符号的游戏上,而必须理解到符号背后代表的意义。理解了这些意义,才能自由地运用符号再现整个思考的过程。
用文科思维来学习数学,其意义就是在符号之外,进一步了解人类如何一步一步把事情「说清楚」的过程。

为什么应该用「文科思维」看待数学?
用「文科思维」学习数学,更重要的不是大量的操练,而是尝试去理解每一个定理背后的证明,以及证明背后的意义。其实这种学习方法才能掌握真正的数学精神,这种数学精神长久以来是西方精神文明的标杆。传说柏拉图学院的门外就树了一个牌子,写着「 不谙几何者不得进内 」。

对古希腊人来说,数学不只是研究特定对象的一门学科,而是一切学科的典型。 一切学科的最高目标就是成为一门数学,或者几何学。因此我们应该从数学学到的,不只是一些计算的技术,而是从中体会西方文明,乃至于现代科学文明的核心精神,理解「知识」,「学问」是如何诞生的。
数学有两个特点一直支配着现代科学对知识和真理的理解: 纯粹性 和 系统性 。
纯粹性 的意思是,数学研究的理念,如数、形状、关系等等,都完全是抽象的,不是任何现实物理世界的对象。正如,理念中的「圆」在现实世界中是不存在的;不论用什么材质、有多精细的工艺,一个现实中圆的东西都不可能是绝对完美的,纯粹的「圆」只存在于理念之中。古希腊数学的进步,使他们发现了在现实世界之上还有一个纯粹的理念世界。柏拉图认为,这个理念世界,或本体世界,比我们生活其中的世界更为真实和完美。现实世界只是对理念的模仿。正是由于理念世界的发现,早期的西方思想家意识到,大自然是可以理解的。世界并不是杂乱无章的,由不可知的神秘力量掌控;它背后有一个可以理解的规律,从此开始了对真理的追寻。
系统性 的意思是,对于一个领域的知识,其实都可以还原为一些基本的概念和公理。系统性科学的典型就是欧几里得的几何学,【几何原本】的重大意义在于,它用了五条简单的公理,就能推理演绎出所有几何学里的定理和命题。这项成就使几何学成为了几乎所有学问的模范,我们现在接触到的科学理论,几乎都是模仿几何学的方式建构的。无论任何学科,最开始都是一些基本的定义和假设,然后这些基本项就如磗块一样,相互构造成整个理论体系。

纯粹性和系统性几乎就是我们当今所学的任何一门学科的基本特征。哪怕是人文学科如历史和文学,其实都离不开这种范式。 历史表面上是对以前社会发生的事的记录和还原,但历史之复杂,以至于我们根本不能在重述历史时不作出选取和解读,在这个过程中,我们关心的就不再只是历史事实,还有历史背后的规律,还有历史事件之间的逻辑关系。文学研究也不只是文学作品的体验,它要求发掘文学作品背后体现出来的时代的人文精神,甚至要找到叙事的基本方式和规律。
不管是文科还是理科,只要它能称得上一门学科,它的功能就在于使用简单和精确的理念来把握复杂的现象,以至于发现现象之间的关系。 而对理念本身的纯粹研究,就是数学。因此,如果你深入理解了一门数学,就能真正理解为什么我们今天的各门学科会被建构成今天这个样子,为什么理念和系统性是一切知识体系的标准。这种理解对我们学习文科也有十分重要的作用。
数学中的想象与永恒
人文精神之所以动人,因为无论是文学,艺术,音乐,历史,乃至宗教,都是一个个活生生的人,运用想象力来迎战生命有限性的斗争故事。面对现实的不完美,我们寄托想象来创造一个完美的世界;面对有限而短暂的人生,我们希望用作品把精神永远流传。

在与命运斗争的历史里,人类总是脆弱的,但在数学里,我们看到一丝希望。
数学能带领我们的想象高飞。如果没有了数学,人类大概不能想象遥远的星空和地上的人间有着一样的运行规律;大概不能想象时间流淌的速度可以改变;大概不能想象有物质没有占有固定的空间位置。。。 我们总以为数学是理性和呆板的,文学是感性和想象的,但现代数学和科学带给我们的想象空间,已经远远超越感性的想象力了。

而且,唯有在数学的领域,我们可以严格的谈论
无限
和
永恒。
作为一个有限的生命,我们可能一生中看到的东西都是有限的,包括日月星辰,高山大海。永恒的造物主高不可攀,永远不向世人现身。但在这个有限的人生里,我们却看到了永恒的数的理念和它们的规律。在数学中,古希腊哲学家第一次看到了无限的可能。这个无限是如何在有限的生命里出现的?这个让人惊叹的问题,一直被视为西方形而上学的核心问题。虽然到现在我们都没有一个明确的答案,但不可否认的是,
数学作为人文精神对永恒追求的实现,值得被所有追求人文价值的人所重视。
*长按关注 哲思时刻,哲学,人文,科普内容定期更新 *










