要快速处理连续碰撞问题,首先要把一些基本的一级结论和二级结论背熟。
一、处理弹性碰撞中的基本方法
一般的复习书中都会给出弹性碰撞的两个守恒式:
m_{1}v_{1}+m_{2}v_{2}=m_{1}v_{1}^{'}+m_{2}v_{2}^{'}; \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}=\frac{1}{2}m_{1}v_{1}^{'2}+\frac{1}{2}m_{2}v_{2}^{'2}
解出:
v_{1}^{'}-v_{2}^{'}=v_{1}-v_{2}
也就是在弹性碰撞中利用动量守恒和机械能守恒可以得到一个等价的式子,那就是
靠近速度=远离速度(符合条件可以作为二级结论使用)
这个式子其实就是恢复系数e=1的等价。
在实际的弹性碰撞中我们往往会扔掉机械能守恒定律的式子,因为它的表达式中关于速度的都是平方,不易求解。
实战中往往写出动量守恒式子和恢复系数为1的式子来联立求解,因为这两个式子中出现的速度都是一次方,求解起来非常方便。
二、弹性碰撞中的一个基本模型——动物撞静物
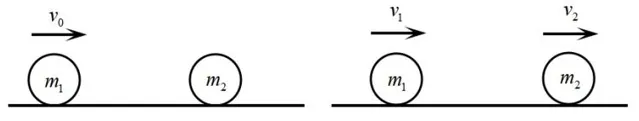

讨论几个特殊情况:

好了,记住以上这些基本结论,让我们开始解题。
三、问题处理
题1.(2020年中国科学技术大学创新班考试物理试题第2题)三个相同的、质量均为m的小滑块(分别编号为1,2,3)排成一行,静止在光滑水平面上,每个滑块之间有间距。现有一质量为M(M>m)的大滑块以速度从左方沿3个小滑块连线的方向射向小滑块,若大滑块与小滑块,小滑块与小滑块之间的碰撞都是完全弹性的,试求所有滑块的最终速度。


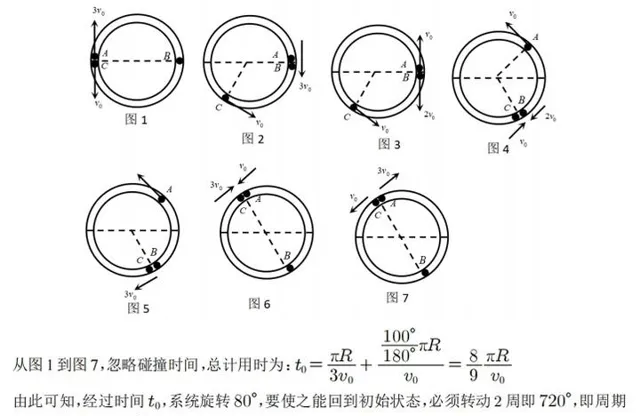
②考虑一个非常有趣的事情,右侧只有1个小滑块,但是小滑块的右侧还有一堵墙,那么小滑块每次碰墙之后从墙那里获得了反向的冲量,再回头撞击M,总有一天会让M向左运动,于是可以命制下题:

解析:这是在2020年左右轰动全世界物理学界的一个碰撞实验。
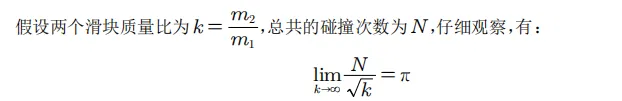
关于上式的证明,可以参考以下文献:
1.程军,孙辉.关于物块碰撞次数的探讨[J].大学物理.2020,39(08):11-13.
2.岳国联等.用矩阵研究一维弹性碰撞与圆周率的关系[J].大学物理.2022,41(08):19-25.
3.陈怡.碰撞出来的圆周率——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论[J].物理与工程.2020,30(01):68-72.
4.文世达等.两球弹性碰撞次数与它们质量之比的关系研究[J].物理通报.2018,(12):120-122.
5.彭定辉.用矩阵方法处理物块碰撞次数问题[J].物理通报.2021,(02):63-64,67.
6.王富强等.一维完全弹性碰撞次数和圆周率[J].物理与工程.2022,32(02):65-73.
7.李开玮.滑块碰撞动力学与圆周率的关联[J].力学与实践.2021,43(01):108-111.
8.许剑伟,吴琼烟.碰撞次数与圆周率[J].湖南中学物理.2022,37(03):73-76.
9.叶志炜黄树清.弹性碰撞与圆周率的奇妙联系[J].物理教学探讨.2022,40(07):59-61.
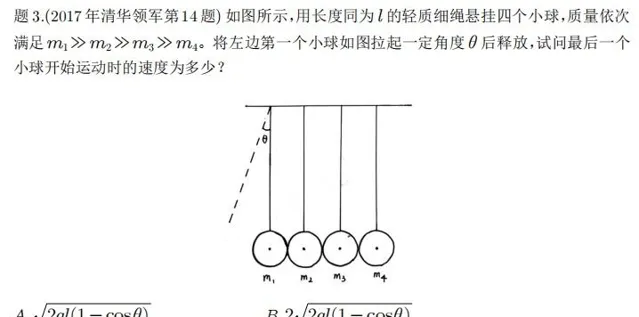
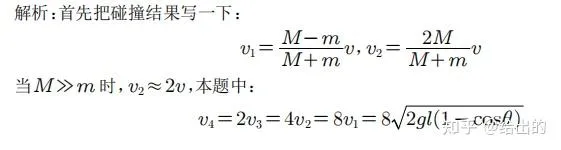









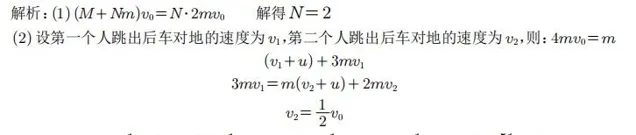
四、结语
连续碰撞问题的处理其实是很套路的,只要记住基本模型的一级结论即可。(需要二级结论和其他高考物理资料可si)











