用于理解局域磁矩形成的关键量,是杂质态的占据数。如果某一种自旋的电子占据态的概率更高,那么这个位点有局域磁矩。通过计算在杂质中发现电子处于系统的给定被占据能量本征态的概率,可以得到杂质位点的占据数。如果 \langle n| 是局域磁矩Hamiltonian H^{\mathrm{A}} 的本征态,具有能量 \epsilon_{n \sigma} ,那么态 |n \sigma\rangle 与杂质位点 |d \sigma\rangle 重叠的概率是 |\langle n \sigma| d \sigma\rangle|^{2} 。由于杂化耦合 V_{\mathbf{k} d} ,这一重叠非零。自旋为 \sigma 的电子在杂质中的净占据数,由对所有能量 \epsilon \leq \epsilon_{\mathrm{F}} 的被占据电子态的求和给出:
\left\langle n_{d \sigma}\right\rangle=\sum_{n, \epsilon_{n \sigma} \leq \epsilon_{\mathrm{F}}}|\langle n \sigma | d \sigma\rangle|^{2}=\int_{-\infty}^{\epsilon_{\mathrm{F}}} d \epsilon \rho_{d \sigma}(\epsilon)\quad \quad (7.5)
杂质中的态密度是
\rho_{d \sigma}(\epsilon)=\sum_{n} \delta\left(\epsilon_{n \sigma}-\epsilon\right)|\langle n \sigma | d \sigma\rangle|^{2}\quad \quad(7.6)
局域磁矩形成的判据是 \left\langle n_{d \sigma}\right\rangle \neq\left\langle n_{d-\sigma}\right\rangle 。
杂质中的相互作用项,导致构造单粒子能级和计算杂质中的态密度变得非平凡。为解决这一问题,我们采用平均场或Hartree-Fock近似,其中单粒子能级是良定义的。由此得到的局域磁矩形成的判据,事实上在预测磁性合金中局域磁矩形成时取得了惊人的成功(GZ1974)。在Hartree-Fock近似下,系统的基态形如
\left|\Phi_{0}\right\rangle=\prod_{\epsilon_{n}<\epsilon_{\mathrm{F}}} a_{n \sigma}^{\dagger}|0\rangle\quad \quad (7.7)
其中,
a_{n \sigma}^{\dagger}=\sum_{\mathbf{k}}\langle\mathbf{k} \sigma | n \sigma\rangle a_{\mathbf{k} \sigma}^{\dagger}+\langle d \sigma | n \sigma\rangle a_{d \sigma}^{\dagger}\quad \quad (7.8)
是能带和杂质态的线性组合。在Hartree-Fock近似下,单体Hamiltonian用新态 (7.8) 写是
H_{\mathrm{HF}}^{\mathrm{A}}=\sum_{n \sigma} \epsilon_{n \sigma} a_{n \sigma}^{\dagger} a_{n \sigma}\quad \quad (7.9)
对Hamiltonian作Hartree-Fock近似,相当于将相互作用项 U n_{\mathrm{d} \uparrow} n_{\mathrm{d} \downarrow} 换成 U\left\langle n_{\mathrm{d} \uparrow}\right\rangle n_{\mathrm{d} \downarrow}+U\left\langle n_{\mathrm{d} \downarrow}\right\rangle n_{\mathrm{d} \uparrow}-U\left\langle n_{\mathrm{d} \uparrow}\right\rangle\left\langle n_{\mathrm{d} \downarrow}\right\rangle ,平均是对态 \left|\Phi_{0}\right\rangle 的。最后一项造成能量零点的整体移动;这不影响局域磁矩的物理,我们扔掉它。缺陷位点的能量重新定义成
E_{d \sigma}=\epsilon_{\mathrm{d}}+U\left\langle n_{d-\sigma}\right\rangle\quad \quad (7.10)
对Anderson Hamiltonian的Hartree-Fock近似是
H_{\mathrm{HF}}^{\mathrm{A}}=\sum_{\sigma} E_{d \sigma} n_{d \sigma}+\sum_{\mathbf{k} \sigma} \epsilon_{\mathbf{k}} n_{\mathbf{k} \sigma}+\sum_{\mathbf{k} \sigma} V_{\mathbf{k} d}\left(a_{\mathbf{k} \sigma}^{\dagger} a_{d \sigma}+a_{d \sigma}^{\dagger} a_{\mathbf{k} \sigma}\right)\quad \quad (7.11)
我们看到,对带在位Coulomb排斥的Hamiltonian作Hartree-Fock近似,相当于位点能的简单重整化; E_{d \sigma} 在局域磁矩形成的平均场论中扮演着重要角色。局域磁矩形成的判据 \left\langle n_{d \sigma}\right\rangle \neq\left\langle n_{d-\sigma}\right\rangle ,等价于 E_{d \sigma} \neq E_{d-\sigma} 。一旦定义了单粒子能级,立刻就能看到 (7.9) 等价于 (7.11) (习题7.3)。
单粒子能量 \epsilon_{n \sigma} 由算符的运动方程定义:
\left[H_{\mathrm{HF}}^{\mathrm{A}}, a_{n \sigma}^{\dagger}\right]=\epsilon_{n \sigma} a_{n \sigma}^{\dagger}\quad \quad (7.12)
为计算上式中的对易子,我们利用
\begin{aligned} \left[H_{\mathrm{HF}}^{\mathrm{A}}, a_{\mathbf{k} \sigma}^{\dagger}\right] &=\sum_{\mathbf{k}^{\prime} \sigma} \epsilon_{\mathbf{k}^{\prime}}\left[a_{\mathbf{k}^{\prime} \sigma}^{\dagger} a_{\mathbf{k}^{\prime} \sigma}, a_{\mathbf{k} \sigma}^{\dagger}\right]+\sum_{\mathbf{k}^{\prime} \sigma} V_{\mathbf{k}^{\prime} d}\left[\left(a_{\mathbf{k}^{\prime} \sigma}^{\dagger} a_{d \sigma}+a_{d \sigma}^{\dagger} a_{\mathbf{k}^{\prime} \sigma}\right), a_{\mathbf{k} \sigma}^{\dagger}\right] \\ &=\epsilon_{\mathbf{k}} a_{\mathbf{k} \sigma}^{\dagger}+V_{\mathbf{k} d} a_{d \sigma}^{\dagger} \end{aligned}\quad \quad (7.13)
以及
\left[H_{\mathrm{HF}}^{\mathrm{A}}, a_{d \sigma}^{\dagger}\right]=E_{d \sigma} a_{d \sigma}^{\dagger}+\sum_{\mathbf{k}} V_{\mathbf{k} d} a_{\mathbf{k} \sigma}^{\dagger}\quad \quad (7.14)
这就得到
\begin{aligned} \left[H_{\mathrm{HF}}^{\mathrm{A}}, a_{n \sigma}^{\dagger}\right] &=\sum_{\mathbf{k}}\langle\mathbf{k} \sigma | n \sigma\rangle\left(\epsilon_{\mathbf{k}} a_{\mathbf{k} \sigma}^{\dagger}+V_{\mathbf{k} d} a_{d \sigma}^{\dagger}\right)+\langle d \sigma | n \sigma\rangle\left(E_{d \sigma} a_{d \sigma}^{\dagger}+\sum_{\mathbf{k}} V_{\mathbf{k} d} a_{\mathbf{k} \sigma}^{\dagger}\right) \\ &=\epsilon_{n \sigma}\left( \sum_{\mathbf{k}}\langle\mathbf{k} \sigma |n \sigma\rangle a_{\mathbf{k} \sigma}^{\dagger}+\langle d \sigma | n \sigma\rangle a_{d \sigma}^{\dagger} \right) \end{aligned}\quad \quad (7.15)
于是有
\epsilon_{n \sigma}\langle\mathbf{k} \sigma | n \sigma\rangle=\epsilon_{\mathbf{k}}\langle n \sigma | \mathbf{k} \sigma\rangle+V_{\mathbf{k} d}\langle d \sigma | n \sigma\rangle\quad \quad (7.16)
以及
\epsilon_{n \sigma}\langle n \sigma | d \sigma\rangle=E_{d \sigma}\langle d \sigma | n \sigma\rangle+\sum_{\mathbf{k}}\langle\mathbf{k} \sigma | n \sigma\rangle V_{\mathbf{k} d}\quad \quad (7.17)
上面两式定义了单粒子能级 \epsilon_{n \sigma} 。具体的解,留作习题(习题7.2),这需要从上面两式中消去 \langle n \sigma | d \sigma\rangle 和 \langle n \sigma | \mathbf{k} \sigma\rangle 。
我们已经展示了,如何得到用于确定态密度的单粒子能级,那么现在具体计算态密度。我们用预解或Green函数进行计算,这直接依赖于杂质能级的展宽。我们先重写态密度,这要用到关系
\begin{aligned} \delta\left(\epsilon-\epsilon_{n \sigma}\right) &=\frac{1}{\pi} \lim _{\Gamma \rightarrow 0} \frac{\Gamma}{\left(\epsilon-\epsilon_{n \sigma}\right)^{2}+\Gamma^{2}} \\ &=\frac{1}{2 \pi \mathrm{i}} \lim _{\Gamma \rightarrow 0}\left[\frac{1}{\epsilon-\epsilon_{n \sigma}-\mathrm{i} \Gamma}-\frac{1}{\epsilon-\epsilon_{n \sigma}+\mathrm{i} \Gamma}\right] \\ &=-\frac{1}{\pi} \lim _{\Gamma \rightarrow 0} \operatorname{Im} \frac{1}{\epsilon-\epsilon_{n \sigma}+\mathrm{i} \Gamma} \end{aligned}\quad \quad (7.18)
于是有
\rho_{d \sigma}(\epsilon)=-\frac{1}{\pi} \lim _{\Gamma \rightarrow 0} \operatorname{Im} \sum_{n} \frac{|\langle n \sigma | d \sigma\rangle|^{2}}{\epsilon-\epsilon_{n \sigma}+\mathrm{i} \Gamma}\quad \quad (7.19)
\left(\epsilon-\epsilon_{n \sigma}+i \Gamma\right)^{-1} 是对应这个问题中Green函数的预解。我们定义Green(算符)函数 G(E+\mathrm{i} \Gamma) 为
(E+\mathrm{i} \Gamma-H) G=1\quad \quad (7.20)
两边同除 (E-H+\mathrm{i} \Gamma) ,用本征态完备基展开 H^{\mathrm{A}} ,得到
G(E+\mathrm{i} \Gamma)=\sum_{n} \frac{|n\rangle\langle n|}{E+\mathrm{i} \Gamma-E_{n}}\quad \quad (7.21)
这是Green函数的谱预解,其中 H|n\rangle=E_{n}|n\rangle , G 具有本征能量 E_n 处的极点奇异性。 G 的本征函数从而是 |n\rangle 。
对单粒子Hamiltonian H=H_{\mathrm{HF}}^{\mathrm{A}} ,我们定义 G 的矩阵元为
\sum_{\beta}(E+\mathrm{i} \Gamma-H)_{\alpha \beta} G_{\beta \mu}=\delta_{\alpha \mu}\quad \quad (7.22)
\alpha,\beta,\mu 标记特定自旋的能带或杂质态,分别是 |\mathbf{k} \sigma\rangle ,|d \sigma\rangle 。由 G 的定义和 (7.19) ,并用 H 的精确本征态写 G ,我们可改写 \rho_{d \sigma}(\epsilon) 为
\begin{aligned} \rho_{d \sigma} &=-\frac{1}{\pi} \lim _{\Gamma \rightarrow 0} \operatorname{Im} \sum_{n} \frac{|\langle n\sigma | d\sigma\rangle|^{2}}{\epsilon-\epsilon_{n \sigma}+\mathrm{i} \Gamma} \\ &=-\frac{1}{\pi} \lim _{\Gamma \rightarrow 0} \operatorname{Im}\langle d \sigma|\mathrm{G}(\epsilon+\mathrm{i} \Gamma)| d \sigma\rangle \\ &=-\frac{1}{\pi} \lim _{\Gamma \rightarrow 0} \operatorname{Im} G_{d d}^{\sigma} \end{aligned}\quad \quad (7.23)
上式联系起态密度和 G 的对角矩阵元,正是我们表述局域磁矩问题所需的主要关系。根据Green函数和约化Hamiltonian满足的方程,我们得到,对 \alpha=\mu=d \sigma 有
\left(\epsilon+\mathrm{i} \Gamma-E_{d \sigma}\right) G_{d d}^{\sigma}-\sum_{\mathbf{k}} V_{d \mathbf{k}} G_{\mathbf{k} d}^{\sigma}=1\quad \quad (7.24)
对 \alpha=k \sigma, \mu=d \sigma 有
\left(\epsilon+\mathrm{i} \Gamma-\epsilon_{\mathbf{k}}\right) G_{\mathbf{k} d}^{\sigma}-V_{\mathbf{k} d} G_{d d}^{\sigma}=0\quad \quad (7.25)
用 (7.25) 从 (7.24) 中消去 G_{d \mathbf{k}}^{\sigma} ,我们得到
G_{d d}^{\sigma}(\epsilon+\mathrm{i} \Gamma)=\left[\epsilon+\mathrm{i} \Gamma-E_{d \sigma}-\sum_{\mathbf{k}} \frac{\left|V_{\mathbf{k} d}\right|^{2}}{\epsilon+\mathrm{i} \Gamma-\epsilon_{\mathbf{k}}}\right]^{-1}\quad \quad (7.26)
如果没有方括号中最后一项, G_{d d}^{\sigma} 的奇异性在重整化位点能 E_{d \sigma} 处。
转移积分 V_{\mathbf{k} d} 展宽了杂质能级。为求出展宽,我们改写 \left(G_{d d}^{\sigma}\right)^{-1} 的最后一项为
\sum_{\mathbf{k}} \frac{\left|V_{\mathbf{k} d}\right|^{2}}{\epsilon-\epsilon_{\mathbf{k}}+\mathrm{i} \Gamma}=\sum_{\mathbf{k}}\left|V_{\mathbf{k} d}\right|^{2} \frac{\epsilon-\epsilon_{\mathbf{k}}-\mathrm{i} \Gamma}{\left(\epsilon-\epsilon_{\mathbf{k}}\right)^{2}+\Gamma^{2}}\quad \quad (7.27)
在 \Gamma \rightarrow 0 的极限下,上式成为
\begin{aligned} \lim _{\Gamma \rightarrow 0} \sum_{\mathbf{k}} \frac{\left|V_{\mathbf{k} d}\right|^{2}}{\epsilon-\epsilon_{\mathbf{k}}+\mathrm{i} \Gamma} &=\mathrm{P}\left(\sum_{\mathbf{k}} \frac{\left|V_{\mathbf{k} d}\right|^{2}}{\epsilon-\epsilon_{\mathbf{k}}}\right)-\mathrm{i} \pi \sum_{\mathbf{k}}\left|V_{\mathbf{k} d}\right|^{2} \delta\left(\epsilon-\epsilon_{\mathbf{k}}\right) \\ &=\mathrm{P}\left(\sum_{\mathbf{k}} \frac{\left|V_{\mathbf{k} d}\right|^{2}}{\epsilon-\epsilon_{\mathbf{k}}}\right)-\mathrm{i} \pi \langle\left|V_{\mathbf{k} d}\right|^{2} \rangle N(\epsilon) \end{aligned}\quad \quad (7.28)
\text{P} 代表主值;在得到最终结果的过程中,我们用到了 (7.18) ,并将 \left|V_{\mathbf{k} d}\right|^{2} 换成它的均值 \langle\left|V_{\mathbf{k} d}\right|^{2} \rangle 。上式中第一项是纯实数,因此代表 d -杂质能级的移动。仅当它作为能量的函数大幅涨落时,这项才影响物理。不过,母体能带的态密度 N(\epsilon) 在 E_{d \sigma} 变化的尺度上相当稳定。那么,上式中实数部分可以忽略, G 成为
G_{d d}^{\sigma}(\epsilon+\mathrm{i} \Gamma)=\frac{1}{\epsilon+\mathrm{i} \Gamma-E_{d \sigma}+\mathrm{i} \Delta}\quad \quad (7.29)
2 \Delta=2 \pi \langle\left|V_{\mathbf{k} d}\right|^{2} \rangle N(\epsilon) 是杂质和传导电子间的有效跃迁速率。
如果将 E_{d \sigma}-\mathrm{i} \Delta 解释成新的位点能,那么 2 \hbar / \Delta 就是杂质能级的寿命。由 (7.23),(7.29) 知, d -杂质中的态密度是Lorentz型的:
\rho_{d \sigma}(\epsilon)=\frac{1}{\pi} \frac{\Delta}{\left(\epsilon-E_{d \sigma}\right)^{2}+\Delta^{2}}\quad \quad (7.30)
正如预期, \Delta 是 d -能级的半宽。
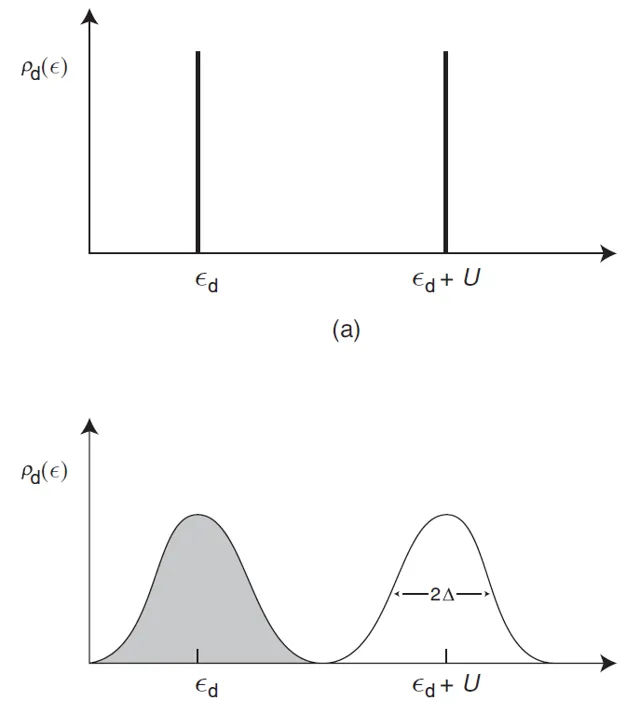
图7.2 (a) d -能级和 k -态间的杂化消失时,Anderson模型中的单粒子态密度。单粒子能 \epsilon_{d} 处的尖峰对应杂质能级未被占据的情形, \epsilon_{d}+U 处的则对应杂质能级已被相反自旋的电子单独占据的情形。在Hartree-Fock层次加入相互作用后,这些峰移到 E_{d \sigma}=\epsilon_{d}+U\left\langle n_{d-\sigma}\right\rangle 处。(b) d 和 k -态混合时的态密度。各态因杂化而展宽。同(a)一样,较低的能级对应杂质能级未被占据的情形,较高的能级则是特定自旋的电子已占据较低能级的情形。如阴影所示,较低能级被占据,较高能级未被占据时,系统有局域磁矩。
d -能级与传导态间的杂化消失时,态密度趋于delta函数。这是为什么?态密度由Green函数的虚部确定。如果随 E 靠近实轴, G(E) 变为纯实数,那么 G(E) 的奇点就是能量上分得很清楚的单极点。这时,态密度对应本征能量 E_{d \sigma}=\epsilon_{d}+U\left\langle n_{d-\sigma}\right\rangle 处的一系列delta函数尖峰。对特定自旋的电子单独占据能级的情形,极点相隔在位Coulomb排斥 U ,如图7.2(a)。如果 d -能级和导带中 k -态间不混合,这种状况将持续。一旦发生混合,极点将偏离实轴,造成纯 d -能级展宽。新的能谱中能级间不再分得很清楚,如图7.2(b)。











