最近看了一些线性代数的文章,关于正交投影(orthogonal projection)在这里做一个小总结,我写的文章通常都比较短,目的是希望在碎片时间能够快速读完并消化。
本文的符号规定:大写字母表示矩阵,如 X,A,Y ,小写字母表示向量,如 \boldsymbol{x},\boldsymbol{y},\boldsymbol{z},\boldsymbol{b} ,如不说明默认都是列向量。
1.为什么要投影
首先,在机器学习中,高维数据通常有这样一些特征:只有少数几个特征包含了整个数据集的大部分信息,其它维通常不是那么重要;其次呢,我们要压缩或者可视化高维数据时,肯定是要做降维处理的,那么为了尽可能地减少这种降维损失,肯定是希望找到那些能够表示数据集大部分信息的维(特征),这方面典型的算法有「主成分分析(PCA,principle component analysis)」,「深度神经网络」。
2.投影的数学定义
定义 :假设 V 是一个向量空间, 并且U 是 V 的一个子空间,有一个线性映射 \pi: V \to U ,该线性映射满足 \pi^2=\pi \circ\pi=\pi , \pi 称为将 V 变到 U 的投影。
PS:学过线性代数的同学都知道,投影矩阵 P 的一个性质是 P^2=P \times P = P ,上述定义的这个线性映射看起来是不是性质相同。
3.向量在向量上的投影
我们从最简单的投影开始讲,一个向量在另一个向量上的投影。在二维平面上,投影如下图所示:
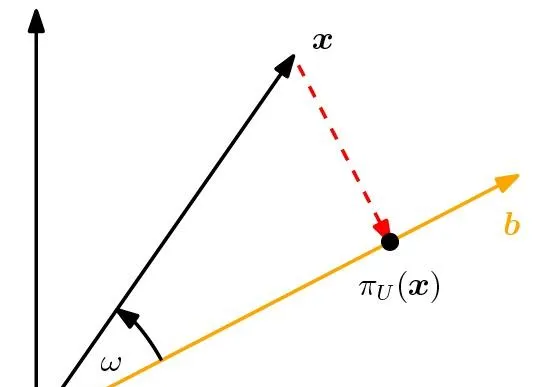
这个和中学时做垂线的道理相同。向量 \boldsymbol{x} \in R^n 在向量 \boldsymbol{b} \in R^n 上的投影记为 \pi_U(\boldsymbol{x}) ,这里 U 是一个一维子空间,为 U=\{ \boldsymbol{x}: \boldsymbol{x}=c \boldsymbol{b}\},c \in R ,也就是这个子空间的向量全部由一个向量 \boldsymbol{b} 张成。投影之后有两点可以确定:
(1)投影 \pi_U(\boldsymbol{x}) 距离最近。所谓距离最近就是在 \boldsymbol{b} 除了 \pi_U(\boldsymbol{x}) 这个向量,找不到其它向量使得它与 \boldsymbol{x} 的距离,即 ||\boldsymbol{x} - \pi{(\boldsymbol{x})}|| 是最小的,从中学的几何我们知道,所谓最近就是垂线最近(因为垂线最短),就是 \boldsymbol{x}-\pi_U(\boldsymbol{x}) 与 \boldsymbol{b} 垂直,也就是线性代数中的正交,用内积表示就是 (\boldsymbol{x}-\pi_U(\boldsymbol{x}))^T \boldsymbol{b}=0 ;
(2)投影 \pi_U(\boldsymbol{x}) 在 U 中,而 U 是由 \boldsymbol{b} 张成的,所以 \pi_U(\boldsymbol{x}) 可由 \boldsymbol{b} 线性表示,即 \pi_U(\boldsymbol{x}) = \lambda \boldsymbol{b}, \lambda \in R 。
3.计算 \lambda 和投影矩阵( P_{\pi} )
(1) \lambda 的计算
因为:
(\boldsymbol{x}-\pi_U(\boldsymbol{x}))^T\boldsymbol{b}=(\boldsymbol{x} - \lambda \boldsymbol{b})^T \boldsymbol{b}=0 \tag{1}
将(1)式展开可得: \boldsymbol{x} ^T \boldsymbol{b} - \lambda \boldsymbol{b}^T \boldsymbol{b}=0 ,从而有:
\lambda = \frac{\boldsymbol{x} ^T \boldsymbol{b} }{\boldsymbol{b}^T \boldsymbol{b}} =\frac{\boldsymbol{b} ^T \boldsymbol{x} }{\boldsymbol{b}^T \boldsymbol{b}} \tag{2}
如果 \boldsymbol{b} 是一个单位向量( ||\boldsymbol{b}|| = 1 ),那么 \lambda = \boldsymbol{b}^T \boldsymbol{x}=\boldsymbol{x}^T \boldsymbol{b} 。
(2)投影矩阵 P_{\pi}
计算 \lambda 后,得到:
\pi_U(\boldsymbol{x}) = \lambda \boldsymbol{b}=\frac{\boldsymbol{b}^T \boldsymbol{x}}{\boldsymbol{b}^T \boldsymbol{b}}\boldsymbol{b}=\boldsymbol{b} \lambda=\boldsymbol{b} \frac{\boldsymbol{b}^T \boldsymbol{x}}{\boldsymbol{b}^T \boldsymbol{b}} = \frac{\boldsymbol{b} \boldsymbol{b}^T }{\boldsymbol{b}^T \boldsymbol{b}} \boldsymbol{x} \tag{3}
从(3)式最后一个等式观察可得到投影矩阵为:
P_{\pi}=\frac{\boldsymbol{b} \boldsymbol{b}^T }{\boldsymbol{b}^T \boldsymbol{b}} \tag{4}
所以,对于任意向量 \mathbf{x} ,它在向量 \mathbf{b} 的投影可以由以下公式计算得到:
\pi_{U}(\boldsymbol{x})=P_{\pi}\boldsymbol{x} \tag{5}
例1 :给定一个向量 \boldsymbol{b}=[1,2,2]^T , \boldsymbol{b} 是一个一维子空间,它代表一个方向,寻找投影矩阵 P_{\pi} ,并计算 \boldsymbol{x}=[1,1,1] 在 \boldsymbol{b} 的投影。
解:由公式(4)得:
P_{\pi}=\frac{\boldsymbol{b} \boldsymbol{b}^T }{\boldsymbol{b}^T \boldsymbol{b}} = \frac{1}{9} \left[\begin{array}{l} 1 \\ 2 \\ 2 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 2 \end{array}\right]= \frac{1}{9}\left[\begin{array}{lll} 1 & 2 & 2 \\ 2 & 4 & 4 \\ 2 & 4 & 4 \end{array}\right]
\boldsymbol{x} 的投影:
\pi_{U}(\boldsymbol{x})=\boldsymbol{P}_{\pi} \boldsymbol{x}=\frac{1}{9}\left[\begin{array}{lll} 1 & 2 & 2 \\ 2 & 4 & 4 \\ 2 & 4 & 4 \end{array}\right]\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]=\frac{1}{9}\left[\begin{array}{c} 5 \\ 10 \\ 10 \end{array}\right] \in \operatorname{span}\left[\left[\begin{array}{l} 1 \\ 2 \\ 2 \end{array}\right]\right]
4.在一般子空间上的投影
注意:粗体的向量需要多输入一些前缀,下面我就不输入了,除非特别说明,否则默认以常规的字母表示。
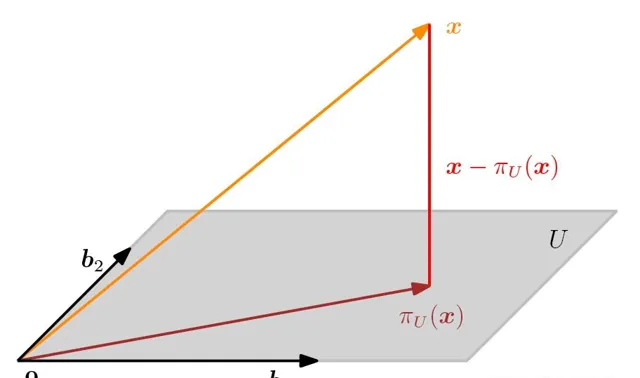
对于一般的子空间 U \in R^n, dim(U)=m \geq 1 ,假设 U 的一个基是 \boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_m ,因为任何向量 \boldsymbol{x} 投影到 U 后所得投影 \pi_U(\boldsymbol{x}) 均在 U 上,因此 \pi_U(\boldsymbol{x}) 可由这组基线性表示:
\pi_U(\boldsymbol{x}) = \sum_{i=1}^{m} \lambda_i \boldsymbol{b}_i = \lambda_1 b_1 + \lambda_2 \boldsymbol{b}_2 + \dots + \lambda_m \boldsymbol{b}_m \tag{6}
其中, \lambda_i \in R,\boldsymbol{b}_i \in R^n,i=1,2,\dots,m 。
令 B = [b_1, b_2,\dots,b_m],\boldsymbol{\lambda}=[\lambda_1, \lambda_2, \lambda_3,\dots, \lambda_m]^T ,改写公式(6)得到:
\pi_U(\boldsymbol{x}) =\sum_{i=1}^{m} \lambda_i \boldsymbol{b}_i = B \boldsymbol{\lambda} \tag{7}
和向量在向量上的投影一样(一维上的投影),在 U 上 \pi_U(\boldsymbol{x}) 也是离 \boldsymbol{x} 是最近的,最近意味着就是最短距离,也就是 \boldsymbol{x}-\pi_U(\boldsymbol{x}) 这个向量垂直(线性空间叫正交)于 U 的任何一个向量,当然也正交于 U 的基 \boldsymbol{b}_1,\boldsymbol{b}_2,\dots,\boldsymbol{b}_m ,所以有:
\begin{aligned} \boldsymbol{b}_1^T(x - \pi_U(\boldsymbol{x})) & = 0 \\ \boldsymbol{b}_2^T(x - \pi_U(\boldsymbol{x})) & = 0 \\ \vdots \\ \boldsymbol{b}_m^T(x - \pi_U(\boldsymbol{x})) & = 0 \end{aligned} \tag{8} <math xmlns="
将公式(7)











