其它答主已经提到时间停止时主角(指代停止时间的角色)的一切运动和思考都是与所谓时间停止相违背的,同时所停止的区域边界也会具有奇性。这也只是在经典力学框架下考量后会得出的问题。我们可以再结合相对论来对该问题进行分析:
(本回答采用几何单位制 c=G=1 ,度规 \eta=\text{diag}(-,+,+,+) )
众所周知在相对论下,时间和空间不是绝对的,它们只是绝对时空的相对分解而已。既然没有绝对的时空分解,那么时间停止事实上并不是那么良好定义的。
考虑最简单的狭义相对论时空: (M,g_{ab})=(\mathbb R^4,\eta_{ab}) ,假设你选择了一个惯性坐标系进行时空分解: M=\Sigma\times\mathbb R(\equiv \mathbb R^3\times\mathbb R) , \{x^\mu\}=\{x^i,t\} ,我们要求空间分解超曲面中开子集 U\subset \Sigma 在 t\in[a,b]= I 之间时间被停止。\color{gray}{我知道回答里每多一个公式,就会有一半人被劝退。防止劝退的最好方法就是量力而行,如果公式看得懂就看,如果不行只看叙述性的结论也是会有收获的}

看起来没什么问题,但当我们换一个惯性系:
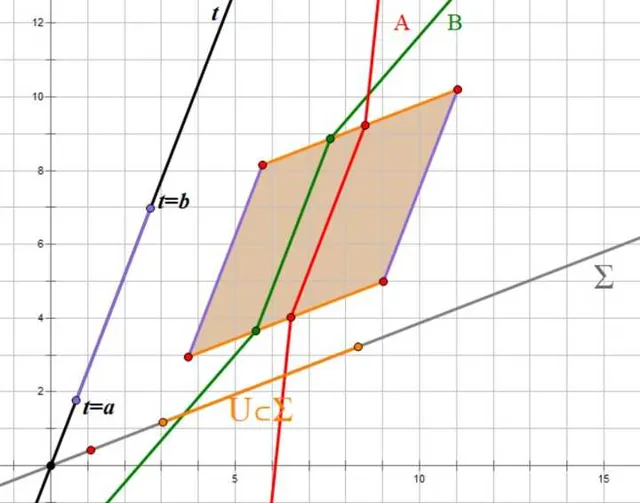
首先新观者可以观察到时间停止区里的一切不论原来观测空间速度为何,在时间停止区内都统一有非0空间速度(这个速度就是新观者观测到的主角停止时间时的空间速度),显然破坏能量守恒,不过在主角停止时间时的随动系里本来能量也不守恒,没必要惊奇,这也是经典力学里可以观测到的情况。但不止如此,新系观测到的「时间停止」空间区域并不是一瞬间区域就全部停止的,而是一个连续地扩散过程。这就是狭义相对论里不同惯性系等时面不同的体现。
由于时空分解的不绝对性,我们有必要对时间停止作一个适当的协变推广(而不是只用时间和空间描述)。我们暂时定义狭义相对论时空中的时间停止是一对数据 (N,U^a) ,其中 N\subset M 为时空中的开子集,而 U^a 是 N 上整体平移的类时归一矢量场(可以代表 N 上的一个「静止」观者,存在性由狭义相对论时空中的度规平直而保证)。在 N 中所有的物理场 \psi|_N 均满足 (\mathscr L_{U}\psi)|_N=0 (沿该观者的李导数为0,代表静止)。 \psi 可以为物质场的动量 p^a ,密度 \rho ,电磁场 F_{ab},A_a 或物质场能动张量 T_{ab} 等等等等。但是不难看到这些物理量在边界处 \partial N 的行为一定是奇异的(导致能量不守恒等),而且该定义其实在涉及时间导数时是不自洽的,不满足相应的运动方程。
我们有办法写出更好的「时间停止」定义,不过这需要我们对「时间」有更好的理解:
相对论里物理上最有意义的且和题目联系最大的时间就是观者的固有时,数学上定义观者(世界线) \gamma:I(\subset\mathbb R)\to M 的固有时 \tau 为观者曲线 \gamma 的弧长 \int_{\gamma}{\sqrt{-g_{ab}T^aT^b}}\mathrm dt=\int_{\gamma}{\mathrm ds} ,其中 T^a=\left(\frac{\mathrm d\gamma}{\mathrm dt}\right)^a 是 \gamma(t) 的切矢,可以理解为观者携带的钟表读数,或观者 所经历的时间 。
还是在狭义相对论时空中,选取惯性坐标系 \{t,x^i\} ,有一观者: \gamma:[0,t_f]\to M ,具有参数: \gamma^\mu(t)=\{t,0,0,0\} ,带入上述定义,有切矢 T^\mu=(1,0,0,0)^\mu ,于是得到该观者的弧长(固有时): \int_{\gamma}{\sqrt{-g_{ab}T^aT^b}\mathrm dt}=\int^{t_f}_0\sqrt{-\eta_{\mu\nu}T^\mu T^\nu}\mathrm dt=\int_0^{t_f}\mathrm dt=t_f 。现在考虑在不改变观者(不改变其世界线)的情况下强迫其固有时缩短,能下手的地方只有 g_{\mu\nu}=\eta_{\mu\nu} ,为时空中的度量结构 g_{ab} 分量。若我们令 U^a=T^\mu(e_\mu)^a ,显然它是类时单位矢,我们定义新度规 g'_{ab}=g_{ab}+(1-\epsilon)U_aU_b ,不难得出 g'_{\mu\nu}T^\mu T^\nu=-\epsilon ,于是该观者固有时就变成了 t_f\int_{\gamma}{\epsilon\mathrm dt} ,只要让 \epsilon 在某个区域外为 1 ,那么时空在该区域外就是正常的,而内部则由标量场 \epsilon 控制时间伸缩。而且在该度规变换下 \{x^i\} 对应的空间几何不变。
而时间静止意味着取 \epsilon\to 0^+ 的极限。但取到该极限后度规退化,使得静止区域不再是物理时空,无法在其上定义观者或类似结构,不过在这种极限下物理场的「时间导数」却是可以自洽为0的(见附录)。
我们现在来具体分析该时间伸缩的效应:
还是取闵氏时空 (\mathbb R^4,\eta_{ab},U_a) , U_a 为该时空中的整体平移类时归一矢量场代表一个静态观者。该静态观者由于超曲面正交自然诱导出一个3+1分解,令度规的空间部分为 h_{ab}=g_{ab}+U_aU_b 。
如法炮制定义新度规 g'_{ab}=g_{ab}+(1-\epsilon)U_aU_b=h_{ab}-\epsilon U_aU_b ,其逆为 g'^{ab}=g^{ab}+(1-\epsilon^{-1})U^aU^b=h^{ab}-\epsilon^{-1}U^aU^b 。
令新度规适配导数算符为 \nabla'_a ,旧导算对应的新联络为: \Gamma^d{}_{ab}=\frac12g'^{cd}(\nabla_ag'_{bc}+\nabla_bg'_{ac}-\nabla_c g'_{ab}) =\frac12g'^{cd}(\epsilon_aU_bU_c+\epsilon_bU_aU_c-\epsilon_c U_aU_b) ,其中 \epsilon_a\equiv(\mathrm d\epsilon)_a ,而新的重伸缩静态观者为 Z^a=\sqrt\epsilon^{-1}U^a , Z_a=\sqrt{\epsilon} U_a 它在新度规下是类时归一的。我们可以计算这些静态观者为了维持静态抵抗几何效应所受的力: F^a=mZ^b\nabla'_bZ^a=mZ^b\nabla_b\sqrt{\epsilon}^{-1}U^a+m\Gamma^a{}_{bc}Z^bZ^c=\epsilon^{-1}\frac m2 h^{ab}(\mathrm d\epsilon)_b
自然牛顿重力在这里的矢量对应就是 F_{(G)}^a=-\epsilon^{-1}\frac m2 h^{ab}(\mathrm d\epsilon)_b ,注意到它是纯空间矢量,我们可以用矢量分析语言写出其3维形式: \vec f_{(G)}=-\frac m2\epsilon^{-1}\vec\nabla\epsilon=-\frac m2\vec\nabla\ln\epsilon
你可能还没有看出什么,但是这个力绝对是猛兽。再重申一遍, \epsilon 代表静态观者 Z^a 的「时间流速」(相对我们之前的 U^a )。如果要使得时空中某一区域 \epsilon 十分接近0,那么它的 \ln\epsilon 就会在时间减速与正常的交界处变化极其剧烈,导致这个力非常大。我们可以再分析它究竟多大:
假设在某一区域( N )内 \epsilon_aU^a=U^a\nabla_a\epsilon=\mathscr L_U\epsilon=0 (时间流速 \epsilon 不随「时间」变化),此时 U^a 显然为 g'_{ab} 的Killing矢量场,(可以用新度规将其降指标 \epsilon U_a 带入Killing方程验证)此时它代表了时间平移对称性,自然可以定义守恒量:能量。注意到对于任意测地线切矢场 T^a 以及Killing矢量场 \xi^a ,有 T^a\nabla'_a(T^b\xi_b)=T^bT^a\nabla'_a\xi_b=T^{(b}T^{a)}\nabla'_{[a}\xi_{b]}=0 ,因此对于任意具有4动量 p^a 的质点,可以定义其能量为 E=-p_aU^a=-\epsilon p^aU_a ,只要该质点不受力(重力不是力),则质点能量守恒。
而观者 Z^a 所观测到的局域能量则是 E_l=-p^aZ_a=-\sqrt{\epsilon}p^aU_a=\sqrt{\epsilon}^{-1}E 。假设质点不受力,则 E 为常数,而 E_l 作为和局域度量结构息息相关的量则可以反应质点3速 v 的大小(国际单位制中有 E_l=\frac{1}{\sqrt{1-v^2/c^2}}mc^2 )。
那么带有静质量 m 的自由质点在 p 点处4动量与 Z^a 同向, E=m\sqrt{\epsilon} ,那么到 q 点时的局域能量差则是 \Delta E_l=m(\sqrt{\frac{\epsilon_p}{\epsilon_q}}-1) ,我们换回国际单位制即 \Delta E_l=mc^2(\sqrt{\frac{\epsilon_p}{\epsilon_q}}-1) , mc^2 的大小我不用多说。很显然哪怕 p 点时间流速是 q 点4倍,多出来的能量都足足有 mc^2 ,照这个比例,要是将一个区域时间减缓到「几乎停止时」空气分子个个都可以向该区域内部方向加速成为Oh my god particle级别的粒子,如果内部时间并没有完全停止,这对于区域内部绝对是毁灭性打击。
同时我们还可以考虑电磁波在该情况下的几何光学近似。由几何光学近似,光子沿类光测地线移动,令其4动量为 P^a=\hbar K^a ,显然也可以定义其守恒能量为 E=-\epsilon P^aU_a=-\sqrt\epsilon P^aZ_a 。注意到光子4波矢 K^a 可以分解为 \omega(Z^a+\hat n^a) ,其中 \omega 为静态参考系 Z^a 观测到的光子角频率, \hat n^a 为朝向光子3波矢的单位矢。于是有 \sqrt\epsilon\omega 守恒,在 p 点测得角频率 \omega_0 的光子在 q 点时则会测得 \omega_0\sqrt{\frac{\epsilon_p}{\epsilon_q}} 。因此当一个区域时间减缓时,在外部看到的内部光会发生红移。当内部时间相对外部几乎停止时,内部光则会发生无限红移,在外部看的确会变成类似黑洞的结构(三体里的黑域也就如此),而在内部所看到的外界光则会无限蓝移,结合上一段的内容,此时内部时空边界处是不稳定的,即使 \epsilon 还未为0时也可能变成具有曲率奇性的位置,显然这是十分病态的。
有答主提到可以干脆改设定,不是将区域时空时间减缓,而是将主角自身时间加快。虽然看上去合理些,但是时间流速差区域仍然存在,可以沿用上述讨论,那么主角的身体和周围的气体就会充当oh my god particle流,我不知道有什么核里的设定可以让主角身体承受这种力,不过我知道的是,地球肯定没了。
【附录】 局域时间停止的标量粒子与拓扑视角的时间停止现象:
考虑标量粒子拉氏密度: \mathcal L=-\frac12(\partial^\mu\phi)(\partial_\mu\phi)-\frac12m\phi^2=-\frac12g^{\mu\nu}(\partial_\mu\phi)(\partial_\nu\phi)-\frac12m\phi^2 ,我们将其进行3+1分解得: \mathcal L=-\frac12 h^{ij}(\partial_i\phi)\partial_j\phi-\frac12m\phi^2+\frac12(\sqrt\epsilon\dot\phi)^2 。若要求粒子在时间停止区 \mathop\lim_{\epsilon\to 0^+} 时作用量在任意紧致区域有限,则等价于要求 (\sqrt\epsilon\dot\phi)^2 有界, \sqrt{\epsilon}\dot\phi=\pm f , \dot\phi=\pm\mathop\lim_{\epsilon\to 0^+}\sqrt{\epsilon}^{-1} f=0 ,在时间停止区其时间导数的确为0。同样的事情发生在其它度规依赖物理场上,因此在 \epsilon 为0的区域里,每条 U^a 的积分曲线上物理场相同,若忽略时间停止区与正常区域之间的交界区,我们可以因此将时间停止区域内所有点按 U^a 的作用建立等价关系: p\sim q\Leftrightarrow \exists r\in\mathbb R(\phi_{U,r}(p)=q,\phi_{U,[0,-r]}^*\epsilon|_p=\{0\}) ,商掉该关系后的新物理时空 M/\sim 具有相同的物理实质,且其上处处度规不退化。由此可以看出,若时间停止区无边,除非存在物理场非度规依赖,否则这种时间停止并不具有物理实质,总可以找到新时空使得时间停止的区域不存在。(再次强调边界项的重要性[doge])











