Plateau's problem(
普拉托问题)
这个问题看上去非常简单,就是问在边界固定的情况下,什么样子的曲面面积最小。这在物理上是一个很显然的问题。根据
普拉托定律,你拿个铁丝弯成边界,然后吹肥皂泡就好了。但是这个在数学上来说,是一门学科,几何测度论(
Geometric measure theory)的核心问题。
为什么说这个问题难呢?我们考虑一个简单的情形,即在三维空间中边界为圆弧的曲面。这个问题答案很显然,就是圆盘。但是从数学角度而言,这个不简单。
通常的想法就是,我们可以把曲面视为一个从二维圆盘到三维空间的映射,然后利用变分法去考虑这个问题。但是这个方法有着很多毛病,其中最大的问题就是缺乏紧性。我们不妨试着跟着这个思路走一下,看看会出怎样的问题。
1. 遍历所有可能的曲面,然后取一个面积趋近于最小(infimum)的序列;
2. 找出一个收敛子序列;
3. 证明极限就是我们想要的曲面,即最小曲面。
在这三步计划中,第二步就会出现很大的问题。比如:
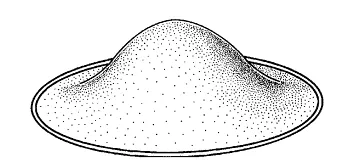
【我是一个有理想的曲面,我的目标是要成为极小曲面】
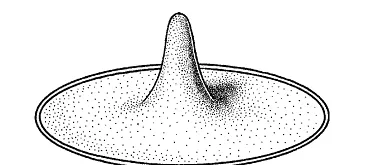
【嗯,我的面积缩小了。感觉好棒!】
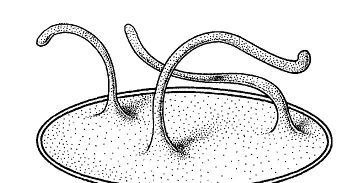
【我的面积又缩小了。可是为什么我感觉怪怪的呢……】

【啊……肯定有……有什么不对……啊……怎么回事……我的面积明明缩小了啊……为什么……我感觉好奇怪啊……不行啊……为什么会变得这么奇怪呢……啊……】
【图片来源:Geometric Measure Theory: A Beginner's Guide 作者:Frank Morgan】
【请绅士们严肃看待这些图片,不要想歪了!也不要「我好兴奋啊」 ! 】
换句话说,即使是曲面的面积在趋近于\pi ,你所取得序列也可能长得非常奇怪,有很多很多的触手(马猴烧酒的好朋友),甚至于这些触手可以触及空间中所有的有理点。换句话说,你最后得到的东西的闭包是整个\mathbb R^3 .
看看,物理中多么显然的东西,在数学中就是这么的让人纠结。存在性就已经够难了,更别说正则性(即最小曲面是否光滑等等)……这个问题直到20世纪中期才有解决方法。具体方法涉及专业知识较多,我自己也不是很熟悉,就不细说了。
其实这种问题很多。比如在给定条件(比如边值)下的拉普拉斯方程
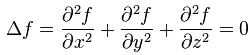
的解的问题。这个问题在物理上也是几乎显然的,因为电势就是解。但是在数学上这个问题并不简单,一般而言需要Sobolev空间等知识进行解决。
【其实我真的不是来黑物理的2333333333 表打我(╯^╰)】
==============2015年5月6日10:31:54(马德里时间)============
那些说我黑数学的人你们够了。请你们仔细思考一下:普拉托定律仅仅是经验性定律,根本无法保证在所有的情况下结论都成立。而数学就是将特殊到一般的过程。
另外,下面的回答中已经有人补充了,数学上关于曲面面积的定义。在上面第二步中,我说找到一族收敛子序列,其实是很不严谨的。因为我没有说是什么收敛,也没有说收敛极限在哪儿。事实上我们需要的极限必须是可求面积的曲面(请跟可求长度的曲线比较起来理解)。所以如何保证极限不会很奇怪,就是存在性的主要工作。











