讲一个调和分析中很经典的反例吧。1917年日本数学家挂谷宗一(Soichi Kakeya)提出了如下的问题:
设某个日本武士在上厕所时被偷袭,他只能挥动长为1的武士刀应战。请问在他将刀挥动一周的过程中,扫过的面积最小为多少?好吧,虽然我觉得问题背景不用叙述得这么具体啦……不过用数学语言描述的话,这其实就是下面的问题:
设平面点集S在每个方向上都含有一条长为1的线段(这样的集合称为Kakeya集),请问S的面积(测度)最小为多少?当然按Kakeya的本意,应该要求长为1的线段能够连续转动(相应的集合称为Kakeya needle集),不过这算是个小的技术问题,暂时不用在意。
经过简单的尝试,容易猜想在凸集情形,最小面积由高长为1的正三角形实现,其值为1/\sqrt{3} ;这点后来被Pál所证明。对于非凸集,Kakeya本人猜测最小面积应由某个三尖内摆线实现,但一直无人能够证明或否认这点。
到了1919年,前苏联数学家Besicovitch在对其他问题的研究中也遇到了上述集合。结果他证明了令人惊讶的结论:
Kakeya集的测度可以为0。这当然完全解决了Kakeya问题;利用Pál的一个技巧,我们可以从测度为0的Kakeya set构造出测度任意小的Kakeya needle集(注意Kakeya needle集的测度不能为0)。因为Besicovitch的贡献,现在我们有时也称Kakeya集为Besicovitch集。
Besicoovitch的构造后来被Perron, Rademacher, Schoenberg,Fisher等人改进过;这里我们介绍一种称为「Perron树」的较为简单的构造。限于篇幅我们只证稍弱一些的结论,即Kakeya集的测度可以任意小。以下证明取自Markus Furtner的学位论文(见[2])。
固定实数\alpha\in(1/2,1) 和正整数k,以|*|表示面积。对任何三角形T,考虑如下的构造步骤:
作T底边上的中线,将T分成两个小三角形L和R。将右边的小三角形R平移至R',使其底边与L重叠,且重叠部分长为T底边长的(1-\alpha) 倍。记T^*=R'\cup L ,由初等几何可证明T^*=B\cup C\cup D ,其中B是与T相似的三角形,相似比为\alpha ;C和D是两个三角形,其面积各为(1-\alpha)^2|T| ,如图所示。为简便起见我们将称B为T^{*} 的「核心」,C和D称为「分支」。
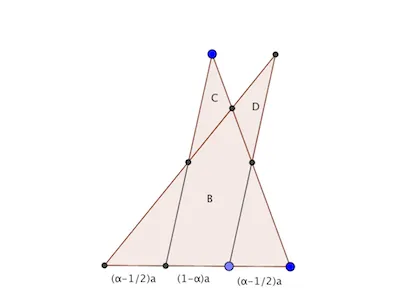
现在取一个高长为1的正三角形T,将T的底边作2^k 等分,记所得的小三角形从左至右为T_0^0,\cdots,T_0^{2^k-1} 。对每个0\leq j\leq 2^{k-1}-1 ,对三角形T_0^{2j}\cup T_0^{2j+1} 进行操作(实际上操作是对两个三角形T_0^{2j} 和T_0^{2j+1} 进行的),设所得图形为S_1^j ,其核心为T_1^{j} 。对0\leq j\leq 2^{k-2}-1 ,容易证明T_1^{2j} 和T_1^{2j+1} (在适当平移后)可以作为某个大三角形对应的L和R,因此对这两个三角形进行操作,得到图形S_2^j (注意,此时S_1^j 的分支部分也进行了相应的平移),设其核心为T_2^j 。如此继续下去,最后得到一个图形S_k^0 。下面我们证明S_k^0 的面积不超过T的面积的\alpha^{2k}+2(1-\alpha) 倍。
实际上,对0\leq m\leq k ,记A_m=\sum_{j=0}^{2^{k-m}-1}|S_m^j| 。首先A_0=|T| ;对于A_1 ,它将等于所有S_1^j 核心与分支部分面积之和。易知核心部分面积之和为\alpha^2|T| ,而分支部分面积之和不超过2(1-\alpha)^2|T| 。因此A_1\leq (\alpha^2+2(1-\alpha)^2)|T| 。对于A_2 ,它不超过所有S_2^j 核心部分与其对应的分支部分面积之和,再加上所有S_1^j 分支部分面积之和。因此A_2\leq (\alpha^4+2\alpha^2(1-\alpha)^2+2(1-\alpha)^2)|T| 。如此下去,我们得到A_k\leq \bigg\{\alpha^{2k}+\sum_{n=0}^{k-1}2\alpha^{2n}(1-\alpha)^2\bigg\}|T|\leq (\alpha^{2k}+2(1-\alpha))|T| ,即所欲证。
现在我们取\alpha 充分接近1,然后取k充分大,即可使S_k^0 的面积任意小。接下来我们证明,对位于T的顶角及其对顶角内的任一方向,S_k^0 均含有该方向上长为1的线段。这实际上是显然的;注意S_k^0 等于T_0^j(0\leq j\leq 2^k-1) 这些小三角形的适当平移的并。因为对所说的任一方向,存在该方向上的一条线段完全位于某个T_0^j 中(只需取从顶角顶点出发,沿该方向的线段),因此也存在该方向上的一条线段完全位于S_k^0 中。
最后我们取S_k^0 的三个适当的旋转的并集,就可以得到面积任意小的Kakeya集。
至此问题就完全解决了。然而当时并没有人意识到,这个集合对调和分析的命运也有很大的关系。当然那就是另外一个故事了。
参考文献:
[1]
https:// en.wikipedia.org/wiki/K akeya_set[2]
http://www. mathematik.uni-muenchen.de /~lerdos/Stud/furtner.pdf










