看了一圈居然没人提这两本神作:
1. Andrea Goldsmith-Wireless Communication
2. David Tse-Fundamentals of Wireless Communication
两本都属于读完樊昌信之后的高阶版本,第一本较全面,Goldsmith是如今站在通信领域金字塔顶端的几个人之一,基本上把物理层的方方面面都写了一遍,也算是紧跟着技术的发展。最后甚至介绍了点网络层的东西。
第二本主要讲MIMO,Tse是伯克利大牛,也是本领域顶级专家,其导师就是Gallager,所以Tse的分量不用我说也清楚了。不要被本书题目骗了以为真的是基础,其实内容非常深,没有数理基础会被虐的很惨。建议先读完第一本再看第二本,都有中文版,但翻译均有很多错误,尤其是第二本翻译很难看,有条件最好读英文版。
这两本书读完之后我最大的一点体会就是,一定要形成信号空间与信号矢量分析的概念(其严格的数学基础来自泛函分析,如果想要深入建议也看一点泛函),樊昌信的书太过初级,从来不强调这一点。读完后你会发现,绝大多数通信问题都能够归结为几何问题,脑子里形成几何图像之后你就会发现很多通信理论是如此简洁美妙。
我这里举一个Tse书中讲AWGN信道容量的例子(这一几何图像最初应该是来自香农那篇著名的论文Communication in the presence of noise),国内的信息论教材一般都是从互信息最大化的角度来推导容量的,这样当然更为严格,但缺乏直观意义。根据采样定理,任何一个带宽为B,时长为T的信号,至少需要N=2BT个样本才能重建,因此可以理解为信号空间近似是N维的,任一接收信号均可以表示为N维欧式空间中的一个点。那么在这样一个N维信号空间里,怎样才能最大化频谱效率?这里就要引用Tse的名言:一个优秀的通信方案应该利用信道中所有可用的自由度。
假设给定发送信号功率约束P ,高斯白噪声的方差为\sigma ^{2} 。根据大数定律,N维接收矢量将以很高概率位于半径等于\sqrt{N(P+\sigma ^{2} ) } 的超球内,对于较大的N,接收矢量同样以较高概率位于发射星座点周围半径等于\sqrt{N} \sigma 的噪声球表面附近。只要接收矢量不相互重叠(亦即接收矢量可以被区分开来)就可以进行可靠的通信,因此不发生重叠的最大星座点数量就是大超球的体积与噪声球体积之比:
\frac{\sqrt{N(P+\sigma ^{2} )} ^{N} }{\sqrt{N\sigma ^{2} }^{N} }
对上式取以2为底的log,就是在T时间内可以传输的最大比特数,再除以T,就可以得到最大速率:
\frac{1}{T} log(\frac{\sqrt{N(P+\sigma ^{2} )} ^{N} }{\sqrt{N\sigma ^{2} }^{N}}) =B log(1+\frac{P}{\sigma ^{2} } )
这就是AWGN信道的容量,相信这个解释能够让人明白「容量」这个词是怎么来的。这一填球模型同样可以形象地说明为什么这个容量是极限值,因为噪声球之间无论如何都会有缝隙,导致信号空间不能被完全填满。
下面这个从Tse的书里截下来的图可以说明问题:
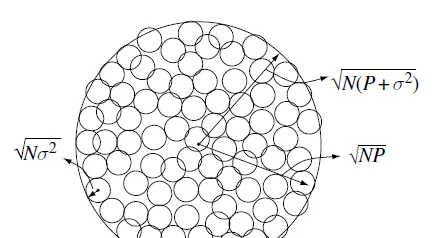
不觉得香农公式实在是太美妙了么?
值得一提的是,Tse和他的弟子Lizhong Zheng把香农这套填球模型从欧式空间推广到了非欧空间。在非相干MIMO通信(Non-coherent MIMO)中,发射机和接收机都不知道信道状态信息(CSI),此时能达到容量的码字X是酉矩阵,假设信道矩阵H为良态的,在接收端,接收码字为Y=HX+W,W为加性高白。高信噪比条件下,由于H未知,Y可以理解为X行向量张成的线性子空间。这一子空间是Grassmann流形上的点,which suggests 接收矢量位于Grassmann流形上,而不是在Rn中。不同于普通AWGN信道,在该场景下,欧式空间中的填球模型将转化为Grassmann流形上的填球模型。Tse和Lizhong Zheng在2002年发表于IEEE Trans on Information Theory上的 "Communication on the Grassmann manifold: a geometric approach to the noncoherent multiple-antenna channel."一文给出了这一模型并求解了容量,该文被引用800余次,并获得了IEEE Information Theory Society当年的Best Paper Award。现在业界很多人提起Lizhong Zheng和Tse的工作一般都只想到分集和复用折中(Diversity-multiplexing tradeoff ),而我个人更喜欢他们的这项工作,非常美妙,也是我最推崇的那种工科理论研究。
我个人的经验是,读教材要抓住一条主线,比如Tse的教材里面freedom degree这个概念贯穿全书。读这些书的时候不妨以「通信系统的几何表征」为主线,并思考如下一些问题,加深对通信问题的几何特性的理解:
1、线性滤波器的「线性」是什么意思?其几何依据是什么?
2、把QAM信号和MPSK信号分成I/Q两路的数学依据是什么?
3、对线性调制的信号进行解调时,解调器中的积分器存在的依据是什么?其几何解释是什么?
4、纠错编码的几何解释是什么?为什么可以减小误码率?
5、CDMA中非正交码(如m序列)和正交码(如沃尔什-哈达玛码)相比有什么好处?
...等等等等。
这些都是通信过程中的基本概念,其几何解释是十分简洁的。可惜这些内容都是我读博士的时候自己看书和思索想到的,本科的时候通信原理老师从来都没有这样和我们讲过,再加上本科不好好学习,专业知识都没学到多少,现在不得不自己补课。以上这些东西我也没有完全搞明白,还在慢慢研究。
希望对你有帮助。











