力学实验4:验证牛顿第二定律实验的两大误差分析
小伙伴们,今天突然想明白了一个道理,或者说想明白了一些事情,人呢,还是要甘于平凡的,但也不用浑浑噩噩,可以不喜欢工作,但要有爱好,像我这样年纪也不小了,依然爱好写一些好玩有趣的物理题目分享给小伙伴们,我快乐,你们也快乐,这就够了,这就是生活了,况且我已经有将近1万的粉丝了,所以更要继续努力了。
生活中有些人就很奇怪,比如领导,领导其实也很肤浅的,比如以写公文为例吧,先不说我写得好不好,领导的评价永远是那么单一,「站位不高」或者「高度不够」,你看,领导都说不出第二种评价标准,哪怕说一句「狗屁不通」也行呀!每次听到「不高」我就「烦躁」,说明这就是官话,就是场面话,就是「无话找话」,从而显得自己「很高」,这样的评价却还要让我来修改,你说气人不,我怎么高,「拔苗助长」吗!
算了,不说了,继续我的分享吧,至少还有小伙伴喜欢看,哈哈!
关于牛顿第二定理这个实验,我在「袁野:力学实验2:探究加速度和力的关系」中有过介绍,今天打算更加详细的说一说并且有所拓展。
关于这个实验原理,这里不再赘述了,重点有二,
1.摩擦误差:平衡摩擦过度或不够。
2.受力误差:就是小车受到的外力并不等于重物的重力,只有当小车质量远远大于重物质量时,才可以认为小车受到的拉力等于重物的重力,所以我们应该记住「大车」。
下面,我们仔细分析这两个误差,可能产生的结果。
一、研究加速度和受力的关系(小车质量不变)
理想情况,小车受到的拉力为 F=mg ,
则, mg=Ma ( M 不变),
即, a=\frac{mg}{M} (理想情况)
当然,上面显然属于理想情况,
下面,我们分析实际情况,
对于摩擦误差,我们以平衡过度考虑,
对于小车受力,也不再是重物重力,而是按照实际情况分析,
从而得到小车的加速度为,
a=\frac{mg+Mg\sinθ-μMg\cosθ}{M+m} (实际情况)
上面的实际加速度公式中同时包含了受力误差和摩擦误差两个方面。
于是,我们把上式区分成两个式子,
(1)当摩擦力平衡时, Mg\sinθ-μMg\cosθ=0 ,则,
a=\frac{mg}{M+m} (只考虑受力误差)
(2)当 M>>m 时,则,
a=\frac{\frac{m}{M}g+g\sinθ-μg\cosθ}{1+\frac{m}{M}}=\frac{m}{M}g+g\sinθ-μg\cosθ (只考虑摩擦(过度)误差)
做出 a-F(mg) 图像如下,
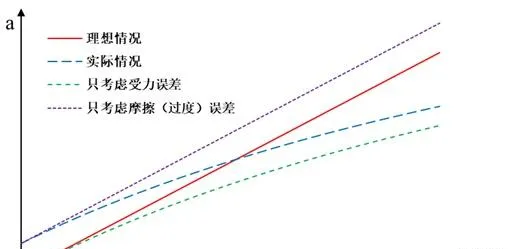
于是,我们发现,对比理想情况,
摩擦(过度)误差主要体现在与纵坐标的截距上,误差为常数,
受力误差主要体现在后半段上,因为在后半段 F(mg) 较大,不满足 M>>m 了,
而反过来说,在前半段则满足 M>>m ,所以只有摩擦误差影响。
二、研究加速度和小车质量的关系(小车受力不变)
这时候,mg 保持不变,我们有两种画图的方法,分别是 a-\frac{1}{M} 图像和 \frac{1}{a}-M 图像。
先说a-\frac{1}{M} 图像,
老样子,写出理想情况,
a =mg·\frac{1}{M} (理想情况)
下面再写出实际情况,
a=\frac{mg+Mg\sinθ-μMg\cosθ}{M+m} (实际情况)
实际情况和之前的式子是相同的,只是换了自变量而已。
我们继续分开考虑,同上面并没有太大区别,
(1)当摩擦力平衡时, Mg\sinθ-μMg\cosθ=0 ,则,
a=\frac{mg}{M+m} (只考虑受力误差)
(2)当 M>>m 时,则,
a=\frac{\frac{m}{M}g+g\sinθ-μg\cosθ}{1+\frac{m}{M}}=\frac{m}{M}g+g\sinθ-μg\cosθ (只考虑摩擦(过度)误差)
作出a-\frac{1}{M} 图像,
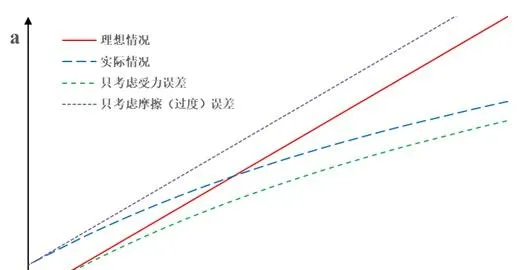
同样,我们发现,对比理想情况,
摩擦(过度)误差主要体现在与纵坐标的截距上,误差为常数,
受力误差主要体现在后半段上,因为在后半段 1/M 较大,即 M 较小,不满足 M>>m 了,
而反过来说,在前半段,则满足 M>>m ,所以只有摩擦误差影响。
然后分析\frac{1}{a}-M 图像时,难度就变大了,或者说有点不一样了。
我们直接给出式子,
\frac{1}{a}=\frac{1}{mg}·M (理想情况)
\frac{1}{a}=\frac{M+m}{mg+Mg\sinθ-μMg\cosθ} (实际情况)
\frac{1}{a}=\frac{M+m} {mg} (只考虑受力误差)
\frac{1}{a}=\frac{M}{mg+Mg\sinθ-μMg\cosθ} (只考虑摩擦(过度)误差)
作出\frac{1}{a}-M 图像,
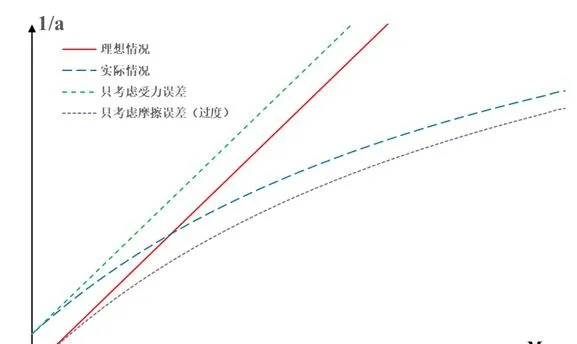
小伙伴们,仔细看上面那个图像,和前面分析的两种情况是有很大区别的,甚至有点相反的,
对比理想情况,
受力误差体现在纵轴截距上,无论是否满足 M>>m ,误差都是常数,
而摩擦误差却体现在了后半段,因为后半段 M>>m ,所以,受力误差影响较小。
小伙伴们,试着尝试自己深入思考一下,要有「高度」哟!
我就讲这么多了,「高度」不够了,哈哈!
最后,送上小礼包一份,祝学业进步,金榜题名!链接:https:// pan.baidu.com/s/1R-YoSi QDz-NaoozVG6jF9Q 提取码:JN95
对了,近期福利大放送,付费咨询只需要1元哟!但是不要问太复杂的题目啦,毕竟时间还是很有限的呀!
好了,小伙伴们,咱们下期再见啦!











