细一看,这不就是一个很经典的金融题目嘛~
已知现金流,折现率,计算NPV,然后看选择投哪个项目嘛。这题我会。
而且既然被邀请了,那就算一下吧。
前提假设
假设在两种情况下,
- 张三(题主)的消费情况类似。
- 张三不会因为生活的富足程度改变生活习惯或者寿命,并且同样都可以活到80岁
- 不考虑税收问题,都为税后收入。
折现率=通胀率=理财预期回报=5%
NPV: Net Present Value 净现值净现值指未来资金(现金)流入(收入)现值与未来资金(现金)流出(支出)现值的差额,是项目评估中净现值法的基本指标。未来的资金流入与资金流出均按预计折现率各个时期的现值系数换算为现值后,再确定其净现值。这种预计折现率是按企业的最低的投资收益率来确定的.是企业投资可以接受的最低界限。 [1]
NPV=∑(CI-CO)(1+i)^(-t)
CI: 收益; CO: 支出; i 折现率; t 时间
上面这段来源于百度。
简单地NPV就是将未来的净收入/净支出 贴现到T0(现在)的值。
第一种情况
在第一种情况先算出总共能够获得的次数
大概是1岁的时候获得25次的收益,然后在68岁的时候获得最后一笔收入。
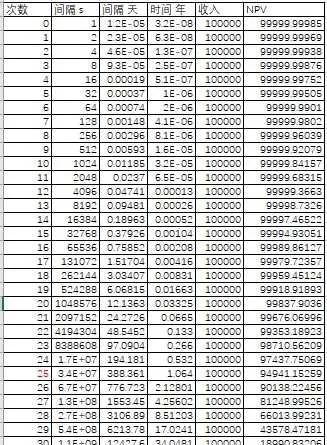
总净现值 NPV_{1} 为2,893,371
总收入(不考虑时间成本)为3,200,000
以下是计算方法:1. 间隔s 代表的是在第几秒的时候可以收到第n次收益=2^n
如张三获得第10次收益的时间为2^10=1024秒
2. 间隔 天 就是简单地把秒换算成天=间隔s/60/60/24
3. 间隔 年 就是再把天数换算成年,= 间隔 天/365 (这里没有考虑闰年的情况,因为不会过多地影响最终答案。)
如在张三想获得第32次收益时,他需要活的年数 = 2^32/60/60/24/365=136.19 (年)
很明显的大于目前的人类平均寿命,故排除。
4. NPV= 收入*(1+5%)^(-t)
第二种情况
工资假设1
假设张三于22岁大学毕业,开始工作。初始工资为8000元每月。
由于他勤勤恳恳地工作,老板大为感动,每年加薪2220元。
并且由于张三是男性,在60周岁时成功退休。
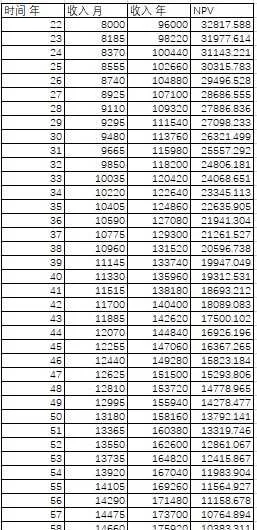
总净现值NPV_{2.1} 为764,880
总收入(不考虑时间成本)为5,389,020
以下是计算方法:收入年=收入月*12
NPV的计算方式同情况1
e.g. 在22岁时的96000元的净现值= 96000*(1+5%)^(-22)=32818
工资假设2
假设张三于22岁大学毕业,开始工作。初始工资为8000元每月。
由于他勤勤恳恳地工作,并且老板不差钱,公司增长业绩喜人,每年升薪5%。
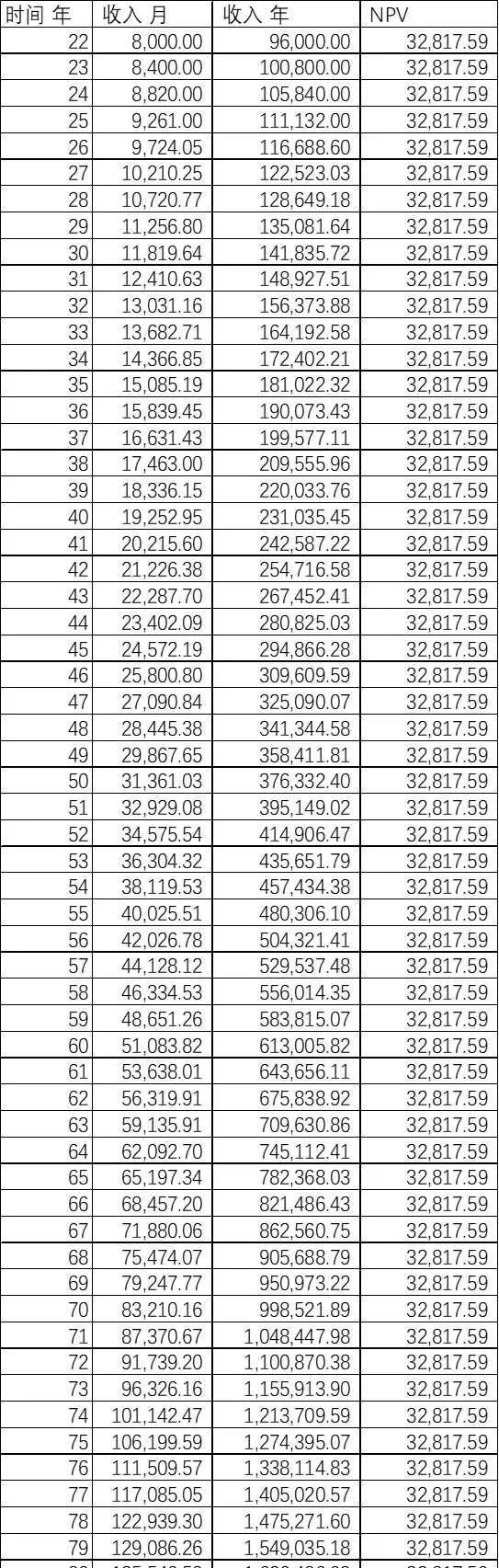
总净现值NPV_{2.2} 为1,936,237.67
总收入(不考虑时间成本)为32,236,225.63
计算方式同工资假设1收入=上一年工资*(1+5%)
工资假设3
假设张三于22岁在世界名牌大学毕业并于毕业后立即开始工作。初始工资为8000元每月。
由于他天资聪颖,技术一流,踏实肯干,持续精进;并且非常幸运地加入到了一家后来成为与鹅厂媲美的独角兽公司;成功公司技术骨干;老板青睐有加;公司业绩持续稳定大幅增长;每年升薪同天朝2009-2019年的平均GDP增幅7.84%。(近两年因为疫情,GDP波动较大,故不引入)
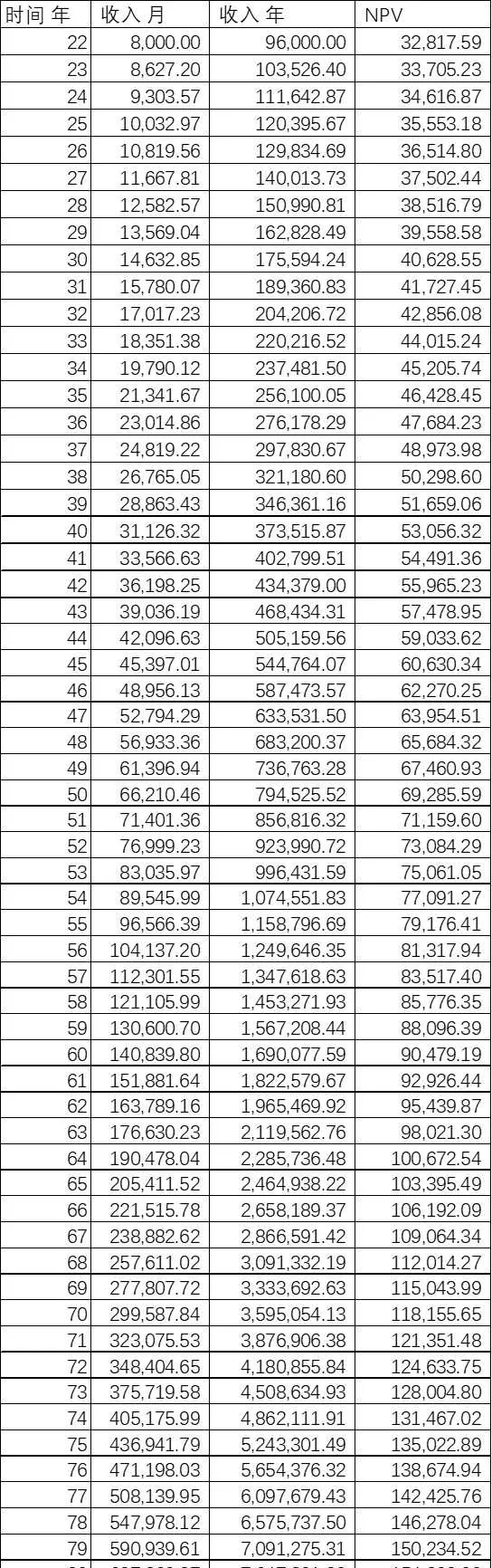
总净现值NPV_{2.3} 为4,645,651.32
总收入(不考虑时间成本)为103,963,957.06
计算方式同工资假设1收入=上一年工资*(1+7.84%)
结论
(NPV_{2.3} =4,645,651.32)>(NPV_{1} =2,893,371 ) >(NPV_{2.2} =1,936,237.67)>( NPV_{2.1} =764,880)
若觉得自己的能力够强,选第二种。
其他情况下,请保守选择第一种。
一些补充说明
一、 货币的时间价值
在这里,细心的朋友应该发现了,张三在第二种情况下其实获得的总收入5,389,020是大于在第一种情况下的总收入3,200,000。 但是为什么我还是推荐选择第一种呢?
为什么今天的100元比1年后的100元更加值钱?1、现时消费,就是早用早享受。
在通胀时期,大多数人都更加倾向于更早地享受这笔钱。
今天买入一只包包,肯定比明年再买这只包包来的爽呀。对小朋友来说,现在吃到1颗糖的快感肯定比1天后吃到同样1颗糖来的高。(即使在通胀=0的情况下也是成立的)
2、货币的潜在收益。也就是机会成本。
钱是可以生钱的。当你存在了银行,又或者是买了理财,这100元在一年后的利息+本金是会大于100元的。又或者你拿这100元在曾经的西子湖畔将这100元投资给了一个姓马的年轻人。
这些可能获得的收益,就是货币的机会成本。
3、通胀导致的货币贬值。 这也就是为什么我们存钱到银行,银行要给你利息。以及为什么我们向银行贷款,我们要付利息给银行。
接着,让我们回到假设。
0岁的张三,将他获得的第一笔10万元存入买入理财。(因为假设中所说通胀率:5%,理财收益率也为5%,那么可以认为这个理财就是无风险的了。)
那么这10万元在他22岁时,就可以获得
10*(1+5%)^22=29.25万
这也就是巴菲特所说的复利的奇迹。
二、NPV
详见第一部分
三、第二种情况的工资增长假设问题。
其实,我最先的假设是每年工资上涨5%,一算后发现到60岁时已经上涨到了61万每年。一想,就算我同意这涨法,张三老板应该不会同意的。
于是就改用了更加符合现实的线性工资增长。工资上限就偷了个懒,直接取了个题目中已知的,中级程序员的巅峰。
如果大家想要更精确地计算的话,可以在这里回复下你们最近5年的工资每年各涨了多少及上涨百分比,有升职的话要标注下哦。我做个比较合乎现实的版本。
不过结论理论上不会差距太大的。毕竟按百分比涨工资的概率太小。
2022/9/28 觉得还是要写一下几个sceneario才显得比较完整,故增加工资增长与通胀持平及与GDP持平的两种状况。四、现实的考量
在现实中,当我们提前拿到了这么一大笔钱之后,我们还会不会乖乖地保持跟工薪族一样的生活,消费习惯呢?
是富不过三代定律: 有钱就变坏,好吃懒做,导致家道中落呢?
还是「凡有的,还要加给他,叫他多余。凡没有的,连他所有的也要夺去。」
利用好第一桶金,好好学习本领让钱滚钱,最后富甲一方呢?
参考
- ^https://baike.baidu.com/item/净现值/500068?fromtitle=NPV&fromid=8832330&fr=aladdin











