
本文創意萱博是自動化控制專業博士,現任職於新加坡某高校。「完美棋盤」是她多年前就曾開過的腦洞。有幸,能在此與各位讀者分享萱博非凡的想象。
從AIphaGo到超現實數,圍棋始終是工程師們的沙盤,數學寶寶們的遊樂場,不過這些科學家研究的物件都是下棋的策略。
今天就讓我們來返璞歸真一下,站在巨人的肩上, 從數學的角度來解讀一下承載這種美麗遊戲的背景——棋盤吧 。

圍棋的棋盤是一個19x19的正方形,我們叫它十九路棋盤,古代的時候也有用十七路棋盤的,小朋友在剛學棋的時候也會用到十三路和九路的棋盤。
我們日常用到的圍棋盤都是這些正方形的。而有些人創造性地使用地圖形狀的棋盤。但是在我看來,這些都不是最完美的棋盤。
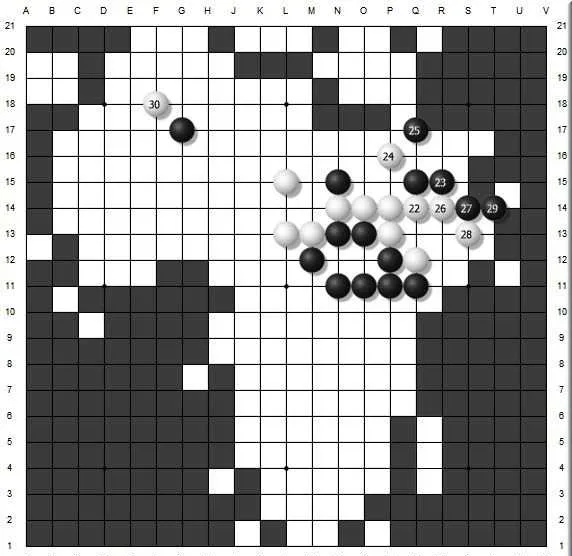
非洲地圖棋盤(原作者:百度貼吧@漫遊的大衛)
完美的棋盤,首先應該沒有「特殊」的交叉點 ——每個交叉點都應該恰好與另外四個交叉點相鄰,不多不少。下面這張同心圓的棋盤就可以滿足此要求:

平面同心圓棋盤
那麽,可以更給力一點嗎?當然是可以的。


上面那張同心圓的棋盤,雖然每個點確實只有四個鄰點,而且沒有了「角」,但還有裏、外兩條「邊」,仍不夠「均勻」。
更完美的棋盤,在沒有棋子的時候,應該是混沌一片,處處都是對稱的。
無論第一手下在哪裏,都是一樣的。
第一手過後才有了兩極,有了策略,有了勝負。
想要這樣的棋盤其實很容易,只需要把這個正方形的棋盤卷一卷,卷成一個圓柱型,然後再折一折,折成一個甜甜圈就可以了。
這裏我們定義1=19, A=T,這樣一個19路的普通棋盤就變成了18路的甜甜圈棋盤。
當然,已經有會玩的棋友想在我前面了,在【 LittleGolem】 這個網站上,就有一場正在進行的甜甜圈圍棋錦標賽,有幾十位棋友參加。

甜甜圈棋盤的平面實作,網路實戰示意圖
上圖的這張棋譜是兩位高水平的愛好者在甜甜圈棋譜上的實戰。
請讀者註意,這張棋盤實際上只有中間橙色的11路,周邊灰色的部份只是輔助對弈者直觀理解甜甜圈棋盤的。
可以看到,如果棋子下在了某一個角上,棋盤的灰色部份也對應地放上三枚棋子。
假設棋子下在了邊上,我們要同時在對面的邊上也放上一樣顏色的棋子。
當然還有計算邊上和角上的棋子的氣的時候,要把對面的那一氣也算進去。
在網路圍棋的時代,要實作這樣一個棋盤太容易了,只需要用上面的定義,就可以把一個看上去方方正正的棋盤卷成一個甜甜圈棋盤。
當然,這樣還有很多不足,比如很多人會習慣性的忽略對手從棋盤的另一面搞突襲。這都是棋子間的距離不夠直觀導致的。
也許正是因為這樣的不足,所以這種理論上完美的棋盤只有少數人在玩。
那麽,可以更更給力一點嗎?當然是可以的。


有沒有可能把甜甜圈圍棋盤搬到現實中來呢?
有一位不願意透露姓名的西方圍棋愛好者,兼能工巧匠,就做出了一個真正的甜甜圈棋盤。

三維甜甜圈棋盤
三十八條交叉的圓形鐵絲,組成了縱橫十九道的甜甜圈棋盤。 這裏的棋子也是特制的,在棋子中心劃出十字槽,可以嵌在交叉點上。
可惜,如此漂亮的實物甜甜圈棋盤,仍有幾處瑕疵。
在這個甜甜圈棋盤上,裏圈的格子特別小,而棋盤的縱線也會比橫線短很多,因此每個格子都不再是正方形的了。
棋盤格子大小不相等,給棋手直觀理解棋局帶來了困難。
比如離某顆棋子最遠的地方在哪裏,這種簡單的策略也需要額外的思考時間。
那麽,可以更更更給力一點嗎?當然還是可以的。


數學上已經有前輩把我們所遇到的這些難題通通解決了, 這個人就是約翰·奈許(John Nash)。
你可能在經濟學領域或者是在他對賽局論的貢獻裏聽說過他的名字。
你也可能看過以他的傳記拍成的電影【美麗心靈】。電影裏有他和好基友在校園裏下圍棋的場景:

電影【美麗心靈】
奈許就是這樣,潤物細無聲地幫我們解決了上文提到的所有問題,但是卻沒有向大家透露,他解決的這些問題與圍棋有什麽關系。
不過我想, 懂一點圍棋和數學的人看到他的嵌入理論(Nash Embedding Theorems)的時候,不難聯想到圍棋的棋盤。

奈許照片
奈許的嵌入理論就是做了兩件事(為了不引入更多術語,我們只討論甜甜圈棋盤這一種情況。無需贅言,嵌入理論可以套用在更廣泛的領域上)。
第一件事,嵌入理論可以把平面的正方形棋盤‘折’成一個類似甜甜圈的形狀,使得棋盤上的每一個格子仍然保持相等的大小。像這樣保持原有圖形距離關系的折疊,數學術語叫做等距對映(isometry)。
這一步用到的具體定理又叫Nash-Kuiper定理,它保證了這種折疊的存在。
而近年,一個名為Heava的法國數學家團隊完成了這種折疊的具體構造,像是一個帶有螺紋裝飾的甜甜圈,見下圖。

精細折疊過的「螺紋甜甜圈」棋盤
實作螺紋甜甜圈的技術挺難的,需要在普通甜甜圈的基礎上做數次名為「起皺」的叠代,相當於一層層地給甜甜圈刻上螺紋。
甜甜圈上螺紋的作用是,使得甜甜圈棋盤上每一格的長寬都相等。下圖給出了折疊前的正方形棋盤,與折疊後螺紋甜甜圈棋盤上曲線的對應關系。
正方形棋盤上原本的縱線(下圖左方黑色縱線),在折疊後變成了螺紋甜甜圈上的一個截面的邊緣(下圖右方黑色的「雪花形」曲線)。
熟悉數學的讀者可能已經看出來,這條雪花形曲線是一種碎形(fractal)。
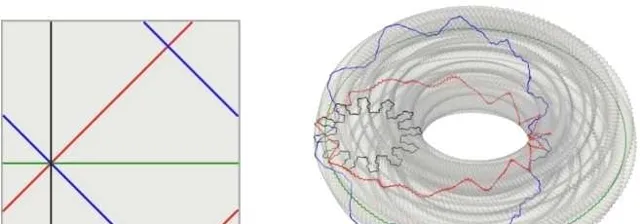
左圖為原正方形棋盤上的三條橫、縱、斜線
右圖為三條線,折疊後在甜甜圈上的形狀與位置
那麽,可以更更更更給力一點嗎?當然仍然是可以的。


我們歷經艱險做出了螺紋甜甜圈形棋盤,但它仍有一個明顯的缺陷: 不夠光滑。
光滑在數學上的含義是,這個曲面上每個點的切面都是可以算出來的。
但是螺紋甜甜圈棋盤,首先它視覺上皺皺巴巴的我們人類不太可能用它下棋。
其次,它數學上也不完美,雖然它每個點的切面都能算出來,但是某些局部的彎曲程度卻是不連續的。
用數學語言說,這些局部的二階導數是無法定義的。
綜上所述,我們必須透過第二步來完善這個棋盤。
當然,得到之前的結果已經很厲害了,手殘黨如我折出的棋盤有棱有角,切面都不能保證存在的呀。

手殘折的有棱有角的棋盤
第二步,把甜甜圈上任意多的點放到一個高維度的歐幾裏得空間,並且保留了原有的甜甜圈上每個點之間的距離關系。
在這個新的高維的棋盤上,棋盤的面確實是平滑的,你可以對每個點算導數算到地老天荒。
而且視覺上,我們上一步被折的皺皺巴巴的棋盤,在這一步重新得以平展開了。
奈許證明了對於甜甜圈這樣的m=2曲面來說,尋找嵌入所需要的維度數不會超過 m^2+5m+3=17維。
不要被這麽高的維度嚇到,這只是一個上限。可以作用於任何形狀的甜甜圈上任意的點。而我們的棋盤可能更特殊,所以幸運的話可能不需要那麽多維度就可以解決問題了。
光說不練假把式。下面就讓我們從4路開始,來體驗一下這個高(維度)大(腦洞)上(檔次)的甜甜圈棋盤吧。

那我們先從5x5的正方形棋盤開始,給每個點都標上座標。註意邊和角的座標都是重復的。一共有16個座標。
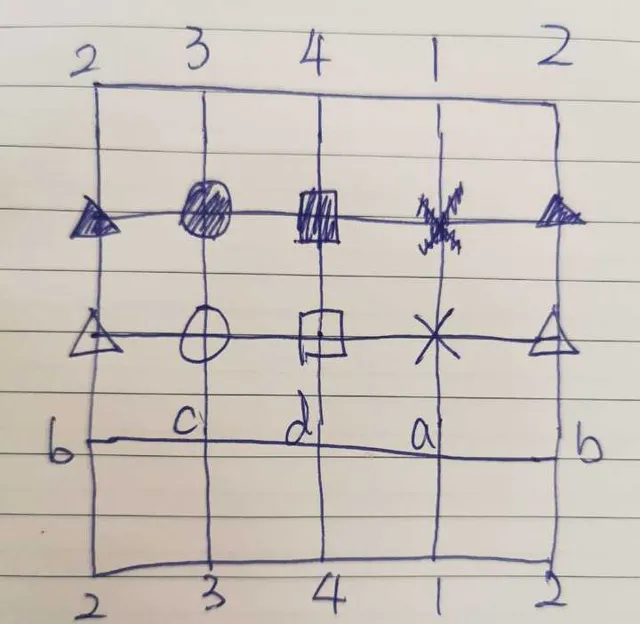
4路平面呈現
然後,我們算一下每兩個點之間的距離,從白色方塊開始我們有可能走出並,尖,單關跳,小飛和象步。但是大飛和拆二就不行了。
然後,我們拿出一個四維的立方體。把立方體的 16個頂點依次標上原來的座標。一個閃閃發光的四維甜甜圈棋盤就做好了。
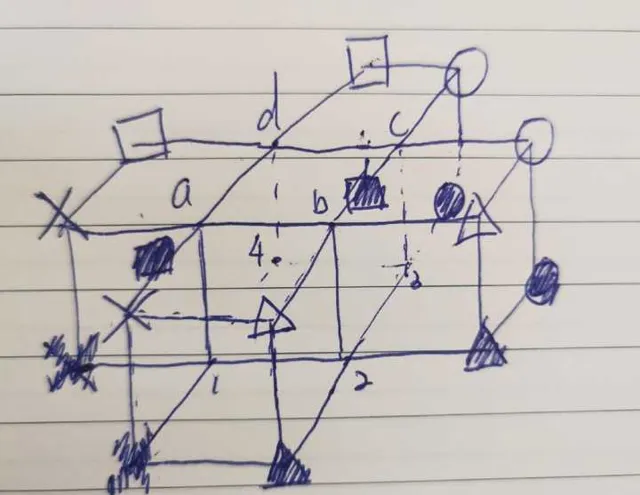
四維上的4路棋盤
驗證一下,在四維立方體上,同樣任意兩點之間的距離,同樣起於白色方塊我們可以得到和平面上一樣的結果。
那麽,能不能更更更更更給力一點呢?

額…… 這個問題,我也遇到困難了。 剛才我示範的是四路棋盤,但更高路數的棋盤,我也不知道答案。
3路棋盤在三維裏的光滑嵌入我猜測是行不通的。
如果4路棋盤需要4維空間實作嵌入,那麽5路棋盤需要幾維空間呢?
17路,19路棋盤,是不是就需要用到最高的17維才能嵌入了呢?
我在這裏拋磚引玉,希望讀者中有大牛能完美地解答這個開放性問題。
不過,無論是這個完美的棋盤是需要嵌入四維空間,還是十七維空間,想在這個棋盤上下棋,首先我們得進入高維空間呢。
讀者朋友們,如果做出了這張完美棋盤,那我們就在高維空間見面下棋吧!
- 暢想和實踐 -


如果智慧化呢?
畢竟這是AI的時代
棋盤自己可以可以跟你下棋,還可以教你下棋,是不是更完美一些?
這個想法在科大訊飛 淘雲科技 ,也在我們心中久久縈繞,歷經多年,前前後後300人參與,終於誕生出一台:

看看實際表現:
 是什麽讓四歲孩子連呼圍棋真好玩
https://www.zhihu.com/video/1859573889149050880
是什麽讓四歲孩子連呼圍棋真好玩
https://www.zhihu.com/video/1859573889149050880
能讓使用者開心喜歡的棋盤,是不是也是一種完美的棋盤?
本文是【 奇略研究所 】原創內容











