基於 gpu 計算德州撲克即時 equity 曲線及轉牌 equity bucket 移動
寫在前面
目前的德州撲克求解器往往基於 CPU,計算時間長,並不適用於即時求解。這些求解器的原理都是遍歷策略樹,根據河牌的結果倒推當前的策略,因此要達到高度的準確性需要巨大的計算量。市面上的實分時析工具僅提供當前可執行的行動,沒有給出玩家的詳細資訊供玩家決策。
因此,我希望開發一個能在短時間內根據範圍繪制權益曲線的工具,並遍歷所有轉牌的組合,分析權益分布的變動情況,再基於經驗制定行動策略。所有向量計算都將基於 GPU 上的 Torch 進行,例如使用 3060 12G 來計算 52 張牌、7 張公共牌和 1.3 億個手牌的排序僅需要 0.05 秒。
為了計算在翻牌時兩手牌的勝率,我們需要遍歷 45 張翻牌和 44 張河牌,共有 990 種組合,分別計算這 990 種情況下兩手牌的排名,並計算勝率。這將需要計算一個具有 1,980 行的張量。
如果計算一手牌對上整個範圍的情況,不考慮手牌之間的相互影響,將需要計算一個具有 2,625,480 行的張量。
而如果計算範圍對上範圍的情況,同樣不考慮手牌之間的相互影響,將需要計算一個具有 3,481,386,480 行的張量。
使用 torch.int8 來儲存張量進行計算,僅保存這些數據就需要約 22GB 的視訊記憶體,實際跑的時候以 80 手牌一個 batch, 視訊記憶體占用就達到了 20 GB,range vs range 的計算一共需要17個batch,4090 計算單個 flop 僅需 10s。我沒有 4090 所以我租了 4 台 4x4090,耗時約4小時,遍歷了22100種翻牌情況,計算出 1326 * 1326 的 equity 矩陣。理論上來說你可以再花45倍的時間連續跑個七八天租伺服器花費14k,儲存空間7TB,你可以跑出所有轉牌的情況,這樣你也可以在毫秒級計算轉牌equity了。
因此現在可以在毫秒級別繪制出翻牌 range vs range 的 equity 曲線。
1import time
2from itertools import combinations
3import matplotlib.pyplot as plt
4import numpy as np
5import poker
6from phevaluator import _evaluate_cards, sample_cards, card
7import pandas as pd
8import seaborn as sns
9import sqlite3
10import torch
11import sys
12sys.path.append('../decisionmaker')
13import evaluator
14from scipy import interpolate
15import math
準備工作
翻前策略是 8max-100std-straddle-no-ante 策略,原格式是 pioviewer 格式的,大約有 9000 多種翻前情況,提前解析好存到柯瑞,就一個客戶端就用sqlite了.
翻前策略轉為 13
13
3 的numpy格式,3 的維度代表 raise allin call 的頻率,然後轉二進制存到資料庫.
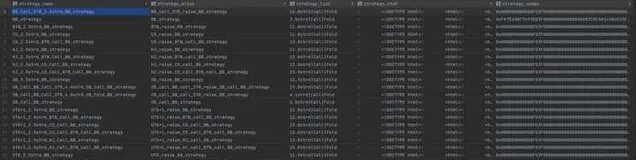
這裏演示 BTN_raise_STR_3b_BTN_call 的行動線.
1# 載入策略
2conn = sqlite3.connect('../example.db')
3cur = conn.cursor()
4str_3b_query = cur.execute("select strategy_numpy from strategy where strategy_name = 'BTN_2.5strd_STR_strategy'").fetchone()
5btn_call_3b_query = cur.execute("select strategy_numpy from strategy where strategy_name = 'BTN_2.5strd_STR_11.0strd_BTN_strategy'").fetchone()
6str_3b_numpy = np.frombuffer(str_3b_query[0]).reshape((13, 13, 3))
7btn_call_3b_numpy = np.frombuffer(btn_call_3b_query[0]).reshape((13, 13, 3))
straddle 位置 AA AKs AQs AJs ATs raise allin call 的頻率
1# str位置面對btn open AA的 raise allin call 頻率
2print(str_3b_numpy.shape)
3print(str_3b_numpy[0,:5])
1(13, 13, 3)
2[[1. 0. 0. ]
3 [1. 0. 0. ]
4 [1. 0. 0. ]
5 [0.588 0. 0.412]
6 [0.148 0. 0.852]]
手牌的 index 對應手牌
| C | D | H | S | |
|---|---|---|---|---|
| 2 | 0 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 | 7 |
| 4 | 8 | 9 | 10 | 11 |
| 5 | 12 | 13 | 14 | 15 |
| 6 | 16 | 17 | 18 | 19 |
| 7 | 20 | 21 | 22 | 23 |
| 8 | 24 | 25 | 26 | 27 |
| 9 | 28 | 29 | 30 | 31 |
| T | 32 | 33 | 34 | 35 |
| J | 36 | 37 | 38 | 39 |
| Q | 40 | 41 | 42 | 43 |
| K | 44 | 45 | 46 | 47 |
| A | 48 | 49 | 50 | 51 |
把策略轉換成所有的組合,如 AKs 轉換成 AcKc AdKd AsKs AhKh 並包裝成 dataframe
1# 手牌的index視覺化
2def card_index_to_human(*index):
3 r = ['2', '3', '4', '5', '6', '7', '8', '9', 'T', 'J', 'Q', 'K', 'A']
4 s = ['c', 'd', 'h', 's']
5 result = [r[i // 4] + s[i % 4] for i in sorted(index, reverse=True)]
6 return "".join(result)
7
8# 手牌範圍的numpy格式轉換為每一個組合 如AKs就轉換為 AcKc AdKd AsKs AhKh四種組合 返回一個pd.df
9# 第一列為手牌組合 第一列為撲克點數 之後為每個行動的頻率
10def range_numpy_to_combo_list(player_range: np.ndarray):
11 # shape 13 13 3
12 hand_list = []
13 for row in range(13):
14 for col in range(13):
15 first_index = 4 * (12 - row)
16 first_list = list(range(first_index, first_index + 4))
17 second_index = 4 * (12 - col)
18 second_list = list(range(second_index, second_index + 4))
19 if row == col:
20 # pair
21 comb_list = list(combinations(range(4 * (12 - row), 4 * (12 - row) + 4), 2))
22 comb_list = [(tuple(sorted(t)), card_index_to_human(*t), player_range[row][col][0], player_range[row][col][1], player_range[row][col][2]) for t in comb_list]
23 hand_list = hand_list + comb_list
24 elif row > col:
25 # offsuit
26 tmp_list = []
27 for i in range(4):
28 for j in range(4):
29 if i != j:
30 tmp_list.append((tuple(sorted((first_list[i], second_list[j]))), card_index_to_human(*(first_list[i], second_list[j])), player_range[row][col][0], player_range[row][col][1], player_range[row][col][2]))
31 hand_list = hand_list + tmp_list
32 else:
33 # suit
34 tmp_list = []
35 for i in range(4):
36 for j in range(4):
37 if i == j:
38 tmp_list.append((tuple(sorted((first_list[i], second_list[j]))), card_index_to_human(*(first_list[i], second_list[j])), player_range[row][col][0], player_range[row][col][1], player_range[row][col][2]))
39 hand_list = hand_list + tmp_list
40 res = pd.DataFrame(hand_list, columns = ['hand', 'human', 'raise', 'allin', 'call'])
41 sorted_df = res.sort_values(by='hand', key=lambda x: x.apply(lambda y: (y[0], y[1]))).reset_index(drop=True)
42 return sorted_df
包裝後的 combo dataframe 共 1326 行,hand 為手牌的 index tuple,然後是各個行動的頻率,index 為 hand 的字典序
1%%time
2str_3b_combo_df = range_numpy_to_combo_list(str_3b_numpy)
3btn_call_3b_combo_df = range_numpy_to_combo_list(btn_call_3b_numpy)
4print(str_3b_combo_df.shape)
5str_3b_combo_df[str_3b_combo_df['raise'] > 0][:5]
1(1326, 5)
2CPU times: total: 0 ns
3Wall time: 14.6 ms
| hand | human | raise | |
|---|---|---|---|
| 241 | (4, 48) | Ac3c | 0.268 |
| 288 | (5, 49) | Ad3d | 0.268 |
| 334 | (6, 50) | Aph | 0.268 |
| 379 | (7, 51) | As3s | 0.268 |
| 383 | (8, 12) | 5c4c | 0.606 |
1%%time
2
3# 根據 flop 的牌面到柯瑞拿到 flop equity matrix
4def get_equity_matrix_from_db(board: tuple):
5 conn = sqlite3.connect(r"E:\project_p\preflop_tips\flop_equity.db")
6 cur = conn.cursor()
7 board = "-".join([str(x) for x in board])
8 query = cur.execute(f"select flop, equity_matrix, mask_matrix from flop_equity where flop = '{board}'").fetchone()
9 conn.close()
10 equity_matrix = np.frombuffer(query[1], dtype=np.float32).reshape((1326, 1326))
11 mask_matrix = np.frombuffer(query[2], dtype=bool).reshape((1326, 1326))
12
13 return equity_matrix, mask_matrix
14
15ALL_COMBINATION = list(combinations(range(52), 2))
16def get_hand_index(hand: tuple):
17 hand = tuple(sorted(hand))
18 return ALL_COMBINATION.index(hand)
1CPU times: total: 0 ns
2Wall time: 0 ns
翻牌
要計算單個手牌對上對手範圍的勝率,用自己這手牌的 index 在 equity matrix 找到所在行,用這一行乘以對手每個組合的手牌占比,然後再按行求和除以本行剔除手牌影響後的組合數,如在 9dThQh 的 flop AhAs 對上 btn_call 範圍的勝率
1%%time
2# 計算單手牌的勝率
3def flop_hand_vs_range_equity(board: tuple, player_1_hand: tuple, player_2_strategy_df: pd.DataFrame, player_2_strategy: str):
4 equity_matrix, mask_matrix = get_equity_matrix_from_db(board)
5 player_1_hand_index = get_hand_index(player_1_hand)
6 player_2_strategy_df['proportion'] = player_2_strategy_df[player_2_strategy] / player_2_strategy_df[player_2_strategy][mask_matrix[player_1_hand_index]].sum()
7 player_2_strategy_df['proportion'] = np.nan_to_num(player_2_strategy_df['proportion'], nan=0.0)
8
9 return np.sum(equity_matrix[player_1_hand_index] * player_2_strategy_df['proportion'].values)
10flop_hand_vs_range_equity((29,34,42), (50, 51), btn_call_3b_combo_df, 'call')
1CPU times: total: 15.6 ms
2Wall time: 54.2 ms
3
4
5
6
7
80.7042426706000064
此函式求出雙方範圍內每一手牌對上對手範圍的勝率和手牌在自己範圍的占比
1# 範圍對上範圍的勝率 player_1_df新增勝率列
2def flop_range_vs_range_equity(board, player_1_strategy_df: pd.DataFrame, player_1_strategy: str, player_2_strategy_df: pd.DataFrame, player_2_strategy: str, *matrix):
3 player_1_strategy_df = player_1_strategy_df.sort_index()
4 player_2_strategy_df = player_2_strategy_df.sort_index()
5
6 if matrix:
7 equity_matrix, mask_matrix = matrix
8 else:
9 equity_matrix, mask_matrix = get_equity_matrix_from_db(board)
10 # 每手牌的權重打橫之後拓展到1326行
11 p1_repeat = np.repeat(player_1_strategy_df[player_1_strategy].values.reshape(1,-1),1326,axis=0)
12 p2_repeat = np.repeat(player_2_strategy_df[player_2_strategy].values.reshape(1,-1),1326,axis=0)
13 # 權重乘以mask矩陣剔除幹涉手牌
14 p1_freq = mask_matrix * p1_repeat
15 p2_freq = mask_matrix * p2_repeat
16 # 每一行權重求和
17 p1_freq_sum = np.sum(p1_freq, axis=1)
18 p2_freq_sum = np.sum(p2_freq, axis=1)
19 # 找出為0的index 避免除0
20 p1_no_zero = np.where(p1_freq_sum != 0)
21 p2_no_zero = np.where(p2_freq_sum != 0)
22 # 構建全0結果矩陣
23 p1_result = np.zeros((1326,))
24 p2_result = np.zeros((1326,))
25 # 求p1對p2的整體勝率 用equity_matrix乘以p2_freq再按行求和
26 equity_matrix_1_vs_2 = np.sum(equity_matrix * p2_freq, axis=1)
27 equity_matrix_2_vs_1 = np.sum(equity_matrix * p1_freq, axis=1)
28
29 p1_result[p2_no_zero] = equity_matrix_1_vs_2[p2_no_zero] / p2_freq_sum[p2_no_zero]
30 p2_result[p1_no_zero] = equity_matrix_2_vs_1[p1_no_zero] / p1_freq_sum[p1_no_zero]
31
32 player_1_strategy_df['equity'] = p1_result
33 player_2_strategy_df['equity'] = p2_result
34
35 player_1_strategy_df['proportion'] = 100 * (np.sum(p1_freq, axis=0) / np.sum(np.sum(p1_freq, axis=0)))
36 player_2_strategy_df['proportion'] = 100 * (np.sum(p2_freq, axis=0) / np.sum(np.sum(p2_freq, axis=0)))
37
38 player_1_strategy_df = player_1_strategy_df[player_1_strategy_df['proportion'] > 0].sort_values(by='equity', ascending=False)
39 player_2_strategy_df = player_2_strategy_df[player_2_strategy_df['proportion'] > 0].sort_values(by='equity', ascending=False)
40
41 player_1_strategy_df['cumsum'] = player_1_strategy_df['proportion'].cumsum()
42 player_2_strategy_df['cumsum'] = player_2_strategy_df['proportion'].cumsum()
43
44 # 構造cumsum 為0 y與equity max一致
45 player_1_strategy_df = pd.concat([pd.DataFrame({'cumsum': [0], 'equity': [player_1_strategy_df.iloc[0]['equity']]}), player_1_strategy_df], ignore_index=True)
46 player_2_strategy_df = pd.concat([pd.DataFrame({'cumsum': [0], 'equity': [player_2_strategy_df.iloc[0]['equity']]}), player_2_strategy_df], ignore_index=True)
47
48
49 return player_1_strategy_df, player_2_strategy_df
雙方範圍計算用 cpu 計算僅需 70 ms 左右,第一行空行是為了繪制 equity 曲線 x = 0 時構造起點
1%%time
2str_3b_equity_df, btn_call_3b_equity_df = flop_range_vs_range_equity((29,34,42), str_3b_combo_df, 'raise', btn_call_3b_combo_df, 'call')
3str_3b_equity_df.head()
1CPU times: total: 62.5 ms
2Wall time: 69.2 ms
| cumsum | equity | hand | human | raise | proportion | |
|---|---|---|---|---|---|---|
| 0 | 0.000000 | 0.926879 | NaN | NaN | NaN | NaN |
| 1 | 0.740942 | 0.926879 | (26, 38) | Jh8h | 0.820 | 0.740942 |
| 2 | 1.136713 | 0.916976 | (37, 46) | KhJd | 0.438 | 0.395771 |
| 3 | 1.532484 | 0.916154 | (38, 45) | KdJh | 0.438 | 0.395771 |
| 4 | 1.928255 | 0.914311 | (39, 46) | KhJs | 0.438 | 0.395771 |
繪制雙方的 equity 曲線,可以看到在這個 flop 我們範圍對上 btn 的範圍整體上都有優勢, 但是堅果優勢不明顯, 我們的手牌 AsAh 大概處於 30% 的位置,在 SRP 的情況下需要高頻過牌,3B 底池低 spr 情況下這個區間的的手牌下註頻率會升高一點
1%%time
2CARD_COMBO = list(combinations(range(52), 2))
3
4# 繪制equity曲線並標記當前手牌的位置
5def paint_equity_curve(p1_df, p2_df, *p1_hand):
6 plt.figure(figsize=(8, 6)) # 設定畫布的大小
7 sns.set_palette("hls") # 設定所有圖的顏色,使用hls色彩空間
8
9 plt.xlabel('Hand_rank', fontsize=15) # 添加x軸標簽,並改變字型
10 plt.ylabel('Equity', fontsize=15) # 添加y軸變淺,並改變字型
11
12 plt.grid(line style='-') # 添加格線
13
14 sns.lineplot(p1_df, x='cumsum', y='equity', color=sns.color_palette("RdBu")[4])
15 sns.lineplot(p2_df, x='cumsum', y='equity', color=sns.color_palette("RdBu")[0])
16 sns.despine(ax=None, top=True, right=True, left=True, bottom=True) # 將影像的框框刪掉
17 if p1_hand:
18 hand_row = p1_df[p1_df['hand'] == tuple(sorted(p1_hand[0]))]
19 plt.scatter(hand_row['cumsum'], hand_row['equity'], color='red', marker='x')
20
21 plt.show()
22paint_equity_curve(str_3b_equity_df, btn_call_3b_equity_df, (50, 51))
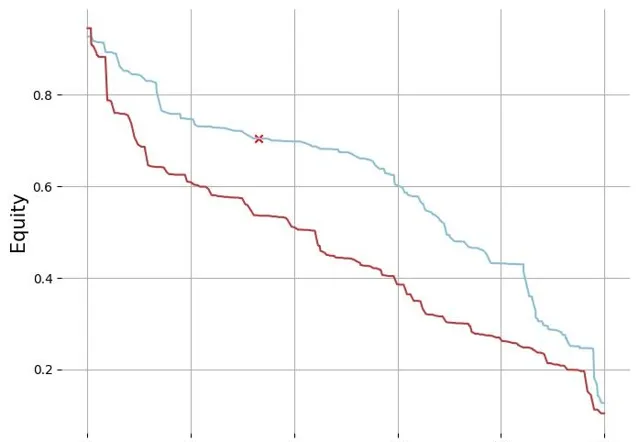
進行插值,然後分別找到兩個範圍的百分位點求插值後繪圖,str equity 領先會在水平線以上,因為 str 的 3B 範圍裏是沒有 KJs 的,所以 str 玩家除了在堅果範圍 equity 落後於 btn 位置玩家,整體都是領先的
1%%time
2# equity差值函式
3def cal_equity_diff(p1_df, p2_df):
4 p1_df_interpolate_func = interpolate.interp1d(p1_df['cumsum'], p1_df['equity'])
5 p2_df_interpolate_func = interpolate.interp1d(p2_df['cumsum'], p2_df['equity'])
6 return p1_df_interpolate_func(list(range(100))) - p2_df_interpolate_func(list(range(100)))
7
8
9# 繪制equity_diff曲線
10def paint_equity_diff_curve(p1_df, p2_df, p1_hand=None):
11
12 diff = cal_equity_diff(p1_df, p2_df)
13 plt.figure(figsize=(8, 6)) # 設定畫布的大小
14 if p1_hand:
15 is_have_hand = p1_df['hand'].loc[1:] == tuple(sorted(p1_hand))
16 if any(is_have_hand):
17 hand_row = str_3b_equity_df.loc[1:][str_3b_equity_df['hand'].loc[1:] == tuple(sorted((50,51)))]
18 plt.scatter(hand_row['cumsum'], diff[int(hand_row['cumsum'].iloc[0])], color=sns.color_palette("RdBu")[0], marker='x')
19
20
21 sns.set_palette("hls")
22 plt.xlabel('Hand_rank', fontsize=15)
23 plt.ylabel('Equity_diff', fontsize=15)
24 plt.axhline(y=0, color=sns.color_palette("RdBu")[0], line style='--')
25 plt.grid(line style='-') # 添加格線
26 sns.lineplot(diff, color=sns.color_palette("RdBu")[4])
27 sns.despine(ax=None, top=True, right=True, left=True, bottom=True) # 將影像的框框刪掉
28
29
30 plt.show()
31hand = (50, 51)
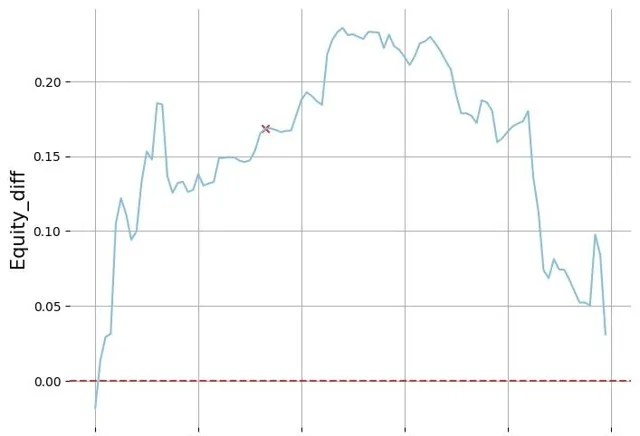
32paint_equity_diff_curve(str_3b_equity_df, btn_call_3b_equity_df, hand)
GPU torch 核心邏輯
1def evaluate_cards_input_torch(cards_tc):
2 hand_size = cards_tc.shape[1]
3 no_flush = NO_FLUSHES[hand_size]
4 hand_count = cards_tc.shape[0]
5
6 # suit_hash = torch.sum(SUITBIT_BY_ID[cards_tc], axis=1)
7 suit_hash = torch.sum(1 << (cards_tc % 4 * 3), axis=1)
8 flush_suit = (SUITS[suit_hash] - 1).reshape((hand_count, 1))
9
10 flush_suit_mask_np = torch.where(flush_suit != -1, True, False).reshape((hand_count,))
11 # 找到 card % 4 == flush_suit 這個條件的index 打標為True
12 #############################################
13 # FLUSH
14 cards_suit = cards_tc % 4
15 # [34, 30, 14, 22, 32]]
16 mask = torch.where(cards_suit - flush_suit == 0, 0x1 << (cards_tc // 4), 0) # n x 5
17 mask_t = mask.t()
18 hand_binary = mask_t[0].to(dtype=torch.int)
19 for i in range(1, hand_size):
20 hand_binary = torch.bitwise_or(hand_binary, mask_t[i])
21 hand_binary = hand_binary.t().reshape((hand_count, 1))
22 flush_result = FLUSH[hand_binary].reshape((hand_count,))
23 #############################################
24 # NO FLUSH
25 # -------------------------------------------
26 cards_rank = cards_tc >> 2
27 cards_rank_t = cards_rank.t()
28 row_counts = torch.zeros((13, cards_rank.shape[0]), dtype=torch.int8, device='cuda:0')
29 rg = torch.arange(cards_rank.shape[0], dtype=torch.int, device='cuda:0')
30 for rank in cards_rank_t:
31 row_counts[rank.to(dtype=torch.int), rg] = row_counts[rank.to(dtype=torch.int), rg] + 1
32 # -------------------------------------------
33 # 轉置之後row為當前rank點數所有手牌組合的array 0 [1 0 1 1 1 1]
34 sum_numb = torch.zeros((1, row_counts.shape[1]), dtype=torch.int, device='cuda:0')
35 num_cards = torch.full((row_counts.shape[1],), hand_size, device='cuda:0')
36 full_tc = torch.full((row_counts.shape[1],), 12, dtype=torch.int, device='cuda:0')
37 for rank, row in enumerate(row_counts):
38 sum_numb = sum_numb + DP[row.to(dtype=torch.int), full_tc - rank, num_cards]
39 num_cards = num_cards - row
40 result = no_flush[sum_numb.t().reshape((hand_count,))]
41 flush = flush_result * flush_suit_mask_np
42 non_flush = result * (~flush_suit_mask_np)
43 return flush + non_flush
44
45def evaluate_fix_flop_turn_matrix(flop: tuple, player_range_1: [tuple], player_range_2: [tuple]):
46 """
47 轉牌一共45張出牌,再遍歷河牌44張出牌計算固定轉牌下的equity matrix
48 :param flop:index tuple (12, 24, 37)
49 :param player_range_1: sorted list index tuple [(19, 26), (19, 27)...]
50 :param player_range_2: sorted list index tuple [(35, 47), (35, 48)...]
51 :return: turn card list [1, 2, 3], ever turn card equity matrix
52 """
53 # 兩個玩家手牌組合的笛卡爾積
54 player_range_cartesian = [lh + rh for lh in player_range_1 for rh in player_range_2]
55 player_range_cartesian_size = len(player_range_cartesian)
56 # 方便找到(13, 45)這種手牌組合在1326個組合中的index
57 helper_index = torch.tensor(reduce(lambda x, y: x + [x[-1] + y], list(range(51, 0, -1)), [0]), dtype=torch.int,
58 device='cuda:0')
59
60 player_hands_tc = torch.tensor(player_range_cartesian, dtype=torch.int8, device='cuda:0').repeat(1, 49) \
61 .reshape(49 * player_range_cartesian_size, -1)
62
63 # 剔除掉flop3張後剩余的牌堆
64 exclude_flop_card = sorted(tuple(set(range(52)) - set(flop)))
65
66 # 構建flop river的固定組合 都是 player_range_cartesian_size * 49 行
67 river_temp_tc = torch.tensor(exclude_flop_card, dtype=torch.int8, device='cuda:0').reshape((49, 1))
68 river_tc = river_temp_tc.repeat(player_range_cartesian_size, 1)
69 flop_tc = torch.tensor(flop, dtype=torch.int8, device='cuda:0').repeat(49 * player_range_cartesian_size, 1)
70
71 # 返回 turn 和 matrix list
72 result_turn_list = []
73 result_equity_matrix_list = []
74 result_mask_matrix_list = []
75 for turn_card in exclude_flop_card:
76 result_turn_list.append(turn_card)
77 turn_tc = torch.tensor(turn_card, dtype=torch.int8, device='cuda:0').repeat(49 * player_range_cartesian_size, 1)
78 # 先不考慮手牌幹涉 合並之後再剔除幹涉組合
79 all_board = torch.cat((flop_tc, player_hands_tc, turn_tc, river_tc), dim=1)
80 # 剔除幹涉的行
81 row_counts = torch.zeros((52, all_board.shape[0]), dtype=torch.int8, device='cuda:0')
82 rg = torch.arange(all_board.shape[0], dtype=torch.int, device='cuda:0')
83 for rank in all_board.t():
84 row_counts[rank.to(dtype=torch.int), rg] = row_counts[rank.to(dtype=torch.int), rg] + 1
85 # 剔除幹涉後hand vs hand river一共有44種出牌
86 interference_mask = ~(torch.max(row_counts, dim=0).values > 1) # 無效置false
87 all_board = all_board[interference_mask]
88
89 player_rank_1 = evaluate_cards_input_torch(all_board[:, [0, 1, 2, 3, 4, 7, 8]])
90 player_rank_2 = evaluate_cards_input_torch(all_board[:, [0, 1, 2, 5, 6, 7, 8]])
91
92 # 每一行為一個組合對上一個組合的勝率
93 single_turn_greater_equity = torch.sum(((player_rank_1 - player_rank_2) < 0).reshape(-1, 44), dim=1) / 44
94 single_turn_equal_equity = 0.5 * torch.sum(((player_rank_1 - player_rank_2) == 0).reshape(-1, 44), dim=1) / 44
95
96 single_turn_greater_equity_t = torch.sum(((player_rank_2 - player_rank_1) < 0).reshape(-1, 44), dim=1) / 44
97 single_turn_equal_equity_t = 0.5 * torch.sum(((player_rank_2 - player_rank_1) == 0).reshape(-1, 44), dim=1) / 44
98 del player_rank_1
99 del player_rank_2
100 base_matrix = torch.zeros((1326, 1326), dtype=torch.float32, device='cuda:0')
101 mask_matrix = torch.zeros((1326, 1326), dtype=torch.int8, device='cuda:0')
102
103 all_board = all_board.reshape(-1, 44, 9)
104
105 base_matrix[
106 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1,
107 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1] \
108 = single_turn_greater_equity + single_turn_equal_equity
109 base_matrix[
110 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1,
111 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1] \
112 = single_turn_greater_equity_t + single_turn_equal_equity_t
113 mask_matrix[
114 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1,
115 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1] \
116 = 1
117 mask_matrix[
118 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1,
119 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1] \
120 = 1
121
122 result_equity_matrix_list.append(base_matrix)
123 result_mask_matrix_list.append(mask_matrix)
124
125 return result_turn_list, result_equity_matrix_list, result_mask_matrix_list
轉牌
遍歷轉牌的所有出牌大概需要3s,計算出每個轉牌的 equity df,繪制每個轉牌的 euiqty 曲線,觀察曲線變化情況
1%%time
2turn_list, equity_matrix_list, mask_matrix_list = evaluator.evaluate_fix_flop_turn_matrix((29, 34, 42), str_3b_equity_df.sort_index()['hand'][1:], btn_call_3b_equity_df.sort_index()['hand'][1:])
1CPU times: total: 2.73 s
2Wall time: 2.91 s
1%%time
2p1_stg_df_list = []
3p2_stg_df_list = []
4
5for index, turn_card in enumerate(turn_list):
6 p1_stg_df, p2_stg_df = flop_range_vs_range_equity((29, 34, 42), str_3b_combo_df, 'raise', btn_call_3b_combo_df, 'call',*(equity_matrix_list[index].cpu().numpy(), mask_matrix_list[index].cpu().numpy()))
7 p1_stg_df['turn'] = turn_card
8 p2_stg_df['turn'] = turn_card
9 p1_stg_df_list.append(p1_stg_df)
10 p2_stg_df_list.append(p2_stg_df)
1CPU times: total: 1.36 s
2Wall time: 1.61 s
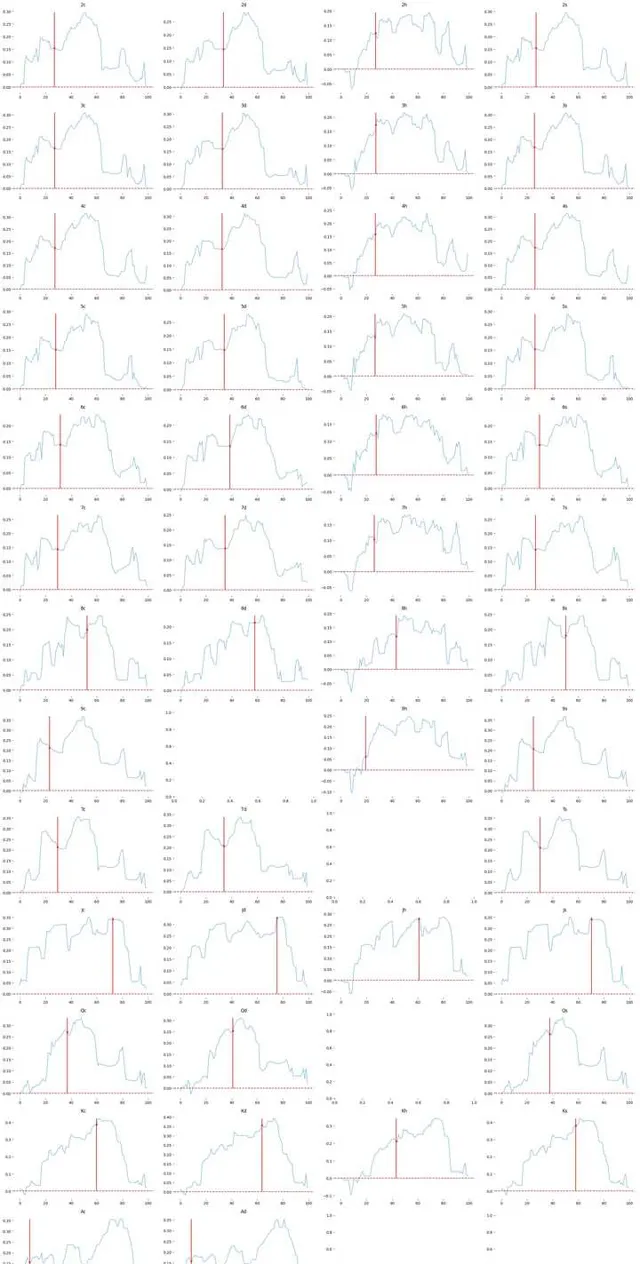
繪制所有轉牌出牌的 equity diff 曲線,每一列代表不同花色,每一行代表不同rank,可以看到轉牌成花之後我們的堅果優勢完全喪失,對方的頂端範圍大量的Ax Kx同花,而在發 8 J K 之後我們的手牌由原來的 30% 區間段後移到 40-60% 區間段,同花順面甚至到 60% 區間段之後.
所有的轉牌只有 A 是對我們有幫助使我們手牌的 equity 位置前移的,所以在我看來 AA 在這個 flop 需要高頻下註來阻止對手實作轉牌的 equity
1hand = (50, 51)
2fig,axes=plt.subplots(13,4, figsize=(24, 49))
3
4for index in range(49):
5 if hand[0] != turn_list[index] and hand[1] != turn_list[index]:
6 diff = cal_equity_diff(p1_stg_df_list[index], p2_stg_df_list[index])
7 sns.set_palette("hls") # 設定所有圖的顏色,使用hls色彩空間
8 hand_row = p1_stg_df_list[index].loc[1:][p1_stg_df_list[index]['hand'].loc[1:] == tuple(sorted(hand))]
9 sns.scatterplot( x=hand_row['cumsum'], y=(diff[math.ceil(hand_row['cumsum'].iloc[0])] + diff[math.ceil(hand_row['cumsum'].iloc[0]) - 1]) / 2,color=sns.color_palette("RdBu")[0],ax=axes[turn_list[index]//4, turn_list[index]%4])
10 sns.lineplot(diff, color=sns.color_palette("RdBu")[4], ax=axes[turn_list[index]//4, turn_list[index]%4]).set_title(card_index_to_human(turn_list[index]))
11 axes[turn_list[index]//4, turn_list[index]%4].axhline(y=0, color=sns.color_palette("RdBu")[0], line style='--')
12 axes[turn_list[index]//4, turn_list[index]%4].set_xlabel("")
13 axes[turn_list[index]//4, turn_list[index]%4].vlines(x=hand_row['cumsum'], ymin=0, ymax=max(diff), color="red")
14 sns.despine(ax=None, top=True, right=True, left=True, bottom=True) # 將影像的框框刪掉
15
16
17plt.tight_layout()
18plt.show()
後續工作
- 目前已經完成了基於 WPK 的翻前提示,但是沒有根據 bet size 來調整翻前範圍,後續會根據對手尺度來調整雙方範圍
- 轉牌的計算邏輯還有最佳化空間,12GB 視訊記憶體計算 SB VS BB 策略範圍太大不分 batch 還是跑不出來
- 繪圖只是方便人類歸納總結,具體策略後續考慮用 RL 來跑,而目前所作的工作可以透過參數餵給它
- 根據 position,spr,equity bucket move 這幾個參數來制定翻後策略
- 感興趣的小夥伴私信聯系啊











