一、選擇題(本大題共10小題,每小題4分,滿分40分)每小題都給出A、B、C、D四個選項,其中只有一個是正確的。
1.(4分)近年來中國芯片技術迅猛發展,麒麟系列芯片突破封鎖,采用先進的7奈米工藝.7奈米=0.000007公釐,將數據0.000007用科學記數法表示為
故選:D.
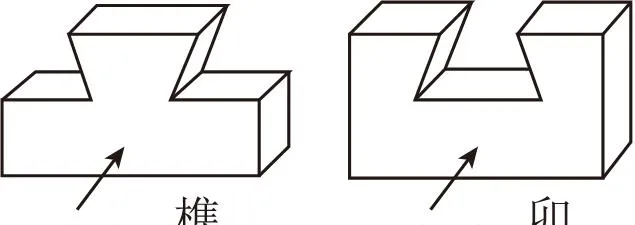
3.(4分)榫卯(sǔnmǎo),是古代中國采用凹凸部位相結合的一種連線方式.在物件上不使用釘子,利用榫卯加固物件,體現出中國古老的文化和智慧.如圖是某種榫卯構件的示意圖,則它們的
A.
B.
C.
D.
∴不等式組的解集為:﹣3≤x<1,
故選:B.
5.(4分)如圖,AB∥DE,∠ABC=80°,∠C=40°,則∠CDE=
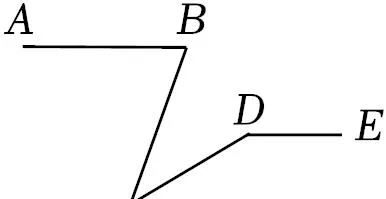
A.120°B.130°C.140°D.150°
【解答】解:延長ED交BC於F,
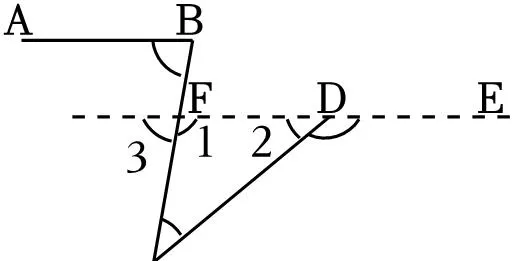
∵AB∥DE,
∴AB∥EF,
∴∠3=∠ABC=80°,
∴∠1=180°﹣∠3=180°﹣80°=100°,
∴∠CDE=∠C+∠1=40°+100°=140°,
故選:C.
【解答】解:根據題意可得:x⊗(x+2)=x(x+2)﹣x,6⊗x=6x﹣6,
∵x⊗(x+2)=6⊗x,
∴x(x+2)﹣x=6x﹣6,
故選:B.
7.(4分)在皖文中學組織舉辦的「唐風宋韻」詩詞大賽中,九年級參賽的25名同學的成績情況如統計圖所示,這些成績的眾數和中位數分別是
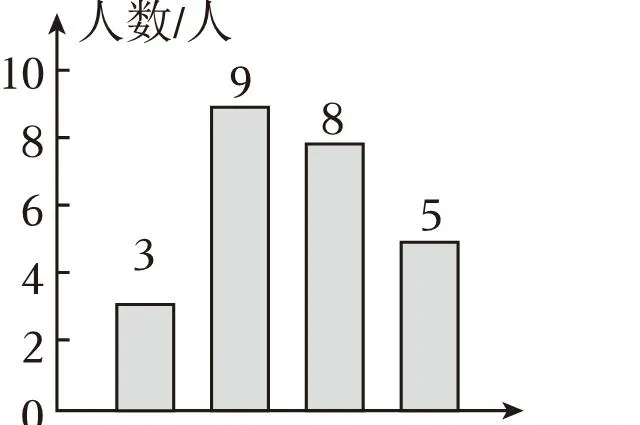
A.98,97B.98,96C.96,98D.96,97
【解答】解:由圖可知:98出現的次數最多,故眾數為98,
按照從小到大排列,第13個數據為96,故中位數為96;
故選:B.
8.(4分)已知四邊形ABCD,對角線AC和BD交於點O,則下列命題是真命題的是
A.如果OB=OD,∠ABC=∠ADC,那麽四邊形ABCD為平行四邊形
B.如果AB=CD,OB=OD,那麽四邊形ABCD為平行四邊形
C.如果AD∥BC,∠ADB=∠CBD,那麽四邊形ABCD為平行四邊形
D.如果AB∥CD,∠ABC=∠ADC,那麽四邊形ABCD為平行四邊形
【解答】解:A、如果OB=OD,∠ABC=∠ADC,不能判定四邊形ABCD為平行四邊形,故本選項不符合題意;
B、如果AB=CD,OB=OD,不能判定四邊形ABCD為平行四邊形,故本選項不符合題意;
C、如果AD∥BC,∠ADB=∠CBD,不能判定四邊形ABCD為平行四邊形,故本選項不符合題意;
D、如果AB∥CD,則∠ABC+∠BCD=180°,再由∠ABC=∠ADC,可得∠ADC+∠BCD=180°,則得到AD∥BC,那麽四邊形ABCD為平行四邊形,故本選項符合題意,
故選:D.
A.B.
C.D.
∴拋物線與x軸相交於(0,0),(2,0),
∴拋物線開口向上,
∴拋物線圖像經過第一、二、四象限,
∴雙曲線圖像位於一、三象限,
∴拋物線與雙曲線交點位於第一象限,即a>0,
∴y=ax+2﹣a必過一、三象限,
∵拋物線與x軸相交於(0,0),(2,0)
∴由圖可知,拋物線與雙曲線交點在(2,0)右邊,
∴a>2,
∴2﹣a<0,
∴直線y=ax+2﹣a的圖像經過一、三、四象限,
故選:A.
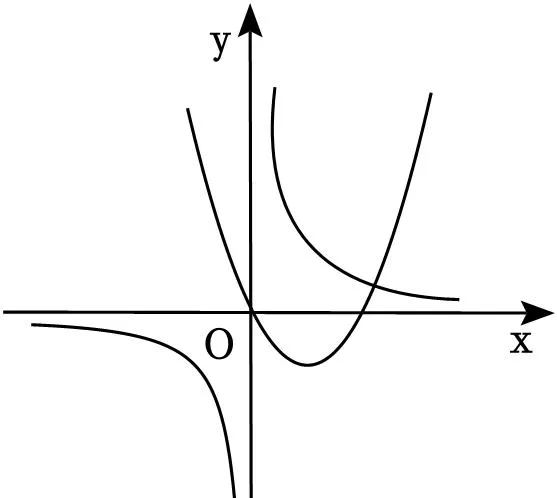
A.CD的最大值是4B.當DE⊥EF時,DE=2
C.CD的最小值是2D.當DE=2時,DE⊥EF
【解答】解:A、如圖:EF,OC相交於點H,連線OE,
∵直線AB與⊙O相切於點C,
∴AB⊥OC,
∵EF∥AB,
∴EF⊥OC,
∵
∴
∴OC=2,
當點C、O、D在同一條直線上時,CD取最大值,此時CD=2OC=4,
故A正確,不符合題意;
C、∵EF⊥OC,
∴CE=CE,
∴∠COF=∠COE=60°,
∵OC=OF=2,
∴△COF是等邊三角形,
∴CF=2,
當點D在CF上時,CD<CF,即CD<2,
故C不正確,符合題意;
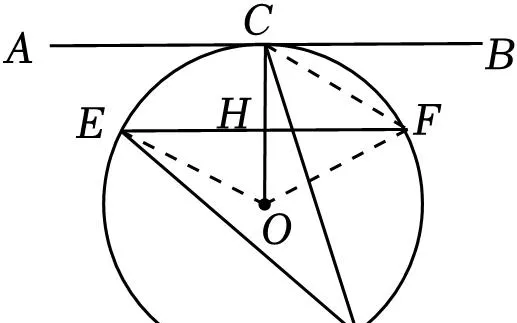
B、連線DF,OD,
∵∠COF=∠COE=60°,OE=OF,
∴∠OFE=30°,
當DE⊥EF時,∠DEF=90°,
∴DF為直徑,則DF=4,
∵OF=OD=2,
∴OF+OD=DF,即點D、O、F共線,
∴∠DFE=30°,
故B正確,不符合題意;
D、當DE=2時,
∵DE=OE=OD=2,
∴△DOE是等邊三角形,則∠DEO=60°,
∴∠OEF=30°,
∴∠DEF=90°,即DE⊥EF,
故D正確,不符合題意;
故選:C.
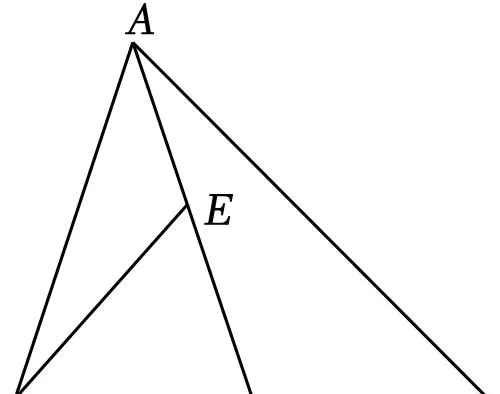
【解答】解:∵AD是中線,BC=6,
∴BD=CD=3,
∵BE=BD,
∴BE=3,∠BED=∠BDE,
∵∠BED=∠ABE+∠BAE,∠BDE=∠DAC+∠C,∠ABE=∠DAC,
∴∠BAE=∠C,
又∵∠ABD=∠CBA,
∴△ABD∽△CBA,
解得:(負值已經舍去).
故答案為:.
∴拋物線對稱軸為直線x=2,
∴點A離對稱軸的距離小於點B離對稱軸的距離,
∵a<0,
∴拋物線開口向下,
∴離對稱軸越遠函式值越小,
故答案為:>;
解得x=1或x=4,
∴x 1 =1,x 2 =4,
∵y 1 ﹣y 2 <3,
∴a+k﹣(4a+k)<3,
∴a>﹣1且a≠0,
故答案為:a>﹣1且a≠0.
=
=
=
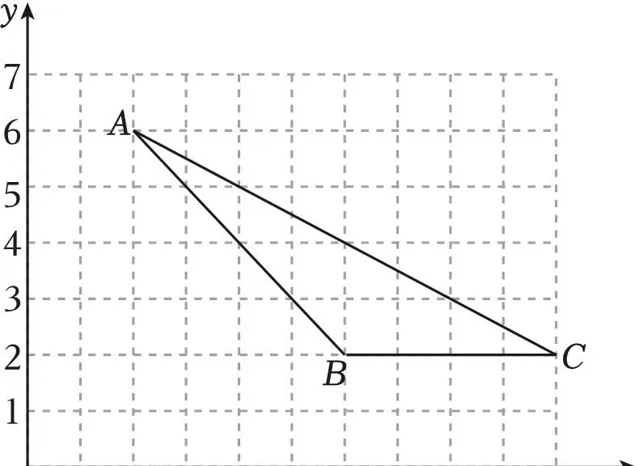
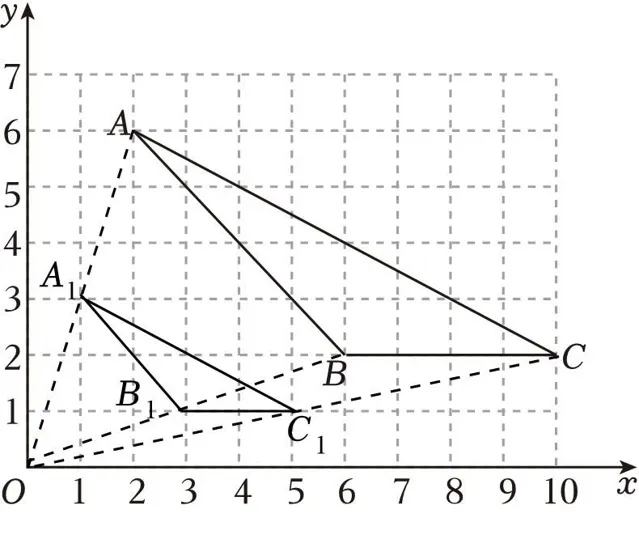
16.(8分)已知△ABC在平面直角座標系中的位置如圖所示,其中點A和點B的座標分別為A(2,6),B(6,2).
四、(本大題共2小題,每小題8分,滿分16分)
17.(8分)某健身達人今年2月份在網上開通直播分享健身經驗和健康飲食,吸引了大批粉絲.2月份新增關註人數為10萬人,4月份新增關註人數為14.4萬人.
(1)求2月份到4月份該健身達人直播的新增關註人數的月平均增長率;
(2)如果能保持這個月平均增長率,則接下來哪一個月該健身達人直播的新增關註人數能達到20萬人?
【解答】解:(1)設新增關註人數的月平均增長率為x,
答:2月份到4月份該健身達人直播的新增關註人數的月平均增長率為20%;
(2)5月份新增關註人數為:14.4×(1+20%)=17.28(萬人),
6月份新增關註人數為:17.28×(1+20%)=20.736(萬人),
答:6月該健身達人直播的新增關註人數能達到20萬人.
18.(8分)鄰邊不相等的矩形紙片,剪去一個正方形,余下一個四邊形,稱為第一次操作;在余下的四邊形紙片中再剪去一個正方形,又余下一個四邊形,稱為第二次操作;……依次類推,若第n次操作余下的四邊形是正方形,操作停止,這樣第n次操作後所得到的余下的正方形則稱為原矩形的n階正方形,如圖,相鄰兩邊長分別為3和5的矩形,最後所得到的正方形為原矩形的3階正方形.

(1)完成上表:
(2)已知矩形的兩相鄰邊長分別為a,b,滿足a=6b+m,b=3m(m為正整數),則最後所得到的正方形是原矩形的 8階正方形.
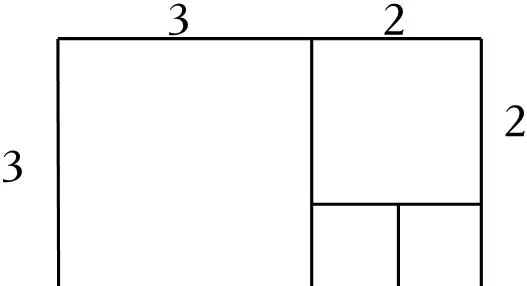
【解答】解:(1)矩形相鄰的兩邊長為3和2時,操作次數為2,最後所得到的正方形為原矩形的2階正方形;
當矩形相鄰的兩邊長為8和3時,如圖:
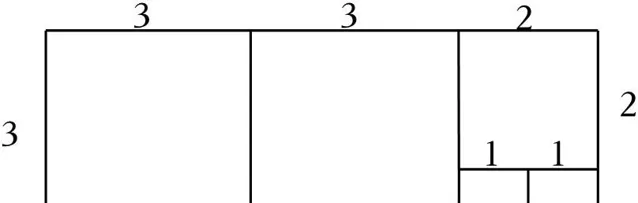
操作次數為4,最後所得到的正方形為原矩形的4階正方形;
填表如下:

(2)a=6b+m,b=3m,
∴a=19m,
如圖:

經過8次操作,最後所得到的正方形為原矩形的8階正方形;
故答案為:8.
五、(本大題共2小題,每小題10分,滿分20分)
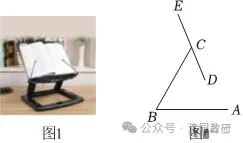
【解答】解:如圖,過點E作EF⊥AB於點F,過點C作CG⊥EF於點G.
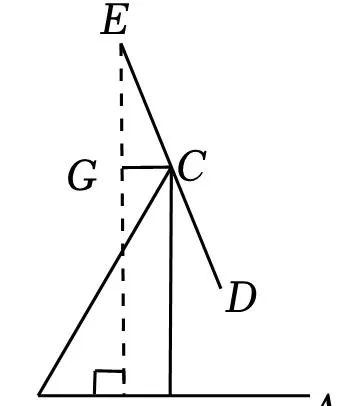
∴四邊形CGFH為矩形,
∴GF=CH,EF∥CH,
∴∠CEG=∠DCH.
∵∠ABC=60°,BC=16cm,
∴∠CEG=∠DCH=∠BCD﹣∠BCH=52°﹣30°=22°.
∵C是DE的中點,
∴
∴
∴EF=EG+GF=7.5+13.84≈21.3cm,即支撐板上的點E到底面AB的距離是21.3cm.
(1)求k,b的值;
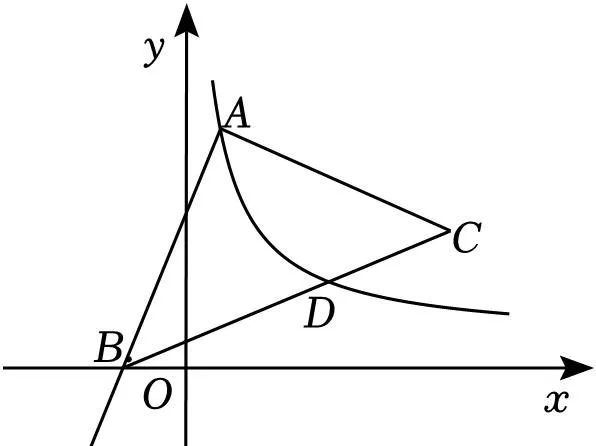
【解答】解:(1)把B(﹣2,0)代入y=2x+b得:0=2×(﹣2)+b,
解得:b=4,
∴該直線的函式解析式為y=2x+4,
把A(m,6)代入y=2x+4得:6=2m+4,
綜上:k=6,b=4.
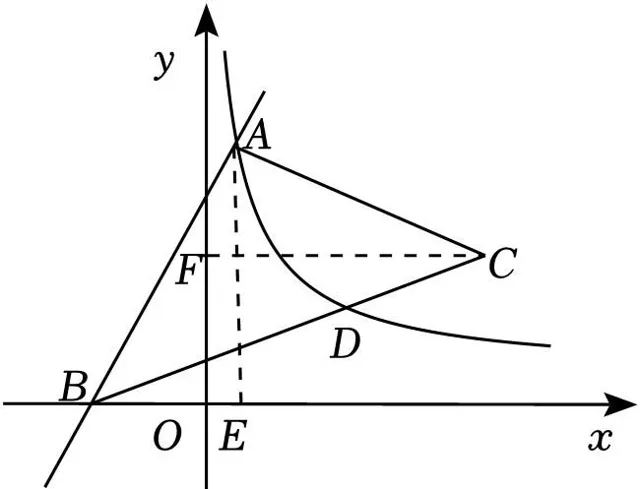
(2)過點A作AE⊥x軸於點E,過點C作CF⊥AE與點F,
∵A(1,6),B(﹣2,0),
∴AO=6,OB=3,
∵AE⊥x軸,CA⊥AB,
∴∠OAB+∠FAC=90°,∠OAB+∠OBA=90°,
∴∠FAC=∠OBA,
∵AE⊥x軸,CF⊥AE,
∴∠AFC=∠BOA=90°,
在△AOB和△CFA中,
∴△AOB≌△CFA,
∴AF=OB=3,AO=CF=6,
∴C(7,3),
設BC所在直線的函式解析式為y=mx+n,
將B(﹣2,0),C(7,3)代入得:
聯立
則
六、(本題滿分12分)
21.(12分)為了了解白龍村村民家庭的用電情況,電力公司抽樣調查了該村村民的每月每戶用電的電費,根據調查結果,繪制出了如下兩個尚不完整的統計圖表.請根據圖表,解答下列問題:
白龍村村民用電情況抽樣調查統計表

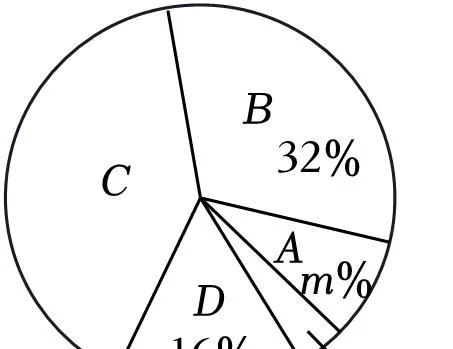
白龍村村民用電情況抽樣調查扇形統計圖
(1)填空:這次被調查的戶數共有 50戶,a+b=28,m=8;
(2)扇形統計圖中扇形C的圓心角度數為 144°;
(3)電力公司擬從小劉、小陳等五名工作人員中任選兩位前往白龍村進行用電安全檢查和指導科學用電,求小劉和小陳至少有一人被選中前往該村的機率.
∴m=8;
故答案為:50,28,8;
(2)360°×(1﹣32%﹣8%﹣4%﹣16%)=144°;
故答案為:144°;
(3)分別用A,B,C,D,E表示小劉、小陳和其他三名工作人員,畫出樹狀圖如圖:
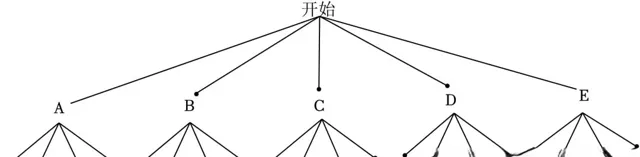
共有20種等可能的結果,其中小劉和小陳至少有一人被選中有14種等可能的結果,
七、(本題滿分12分)
(1)求p關於x的函式關系式;
(2)求等待觀光車的遊客最多時有多少人?
當5<x≤8時,p=50x+1550﹣20x×12=﹣190x+1550,
∵a=﹣20<0,
∴當x=4時,p有最大值620;
當5<x≤8時,p=﹣190x+1550,
把x=5代入得,p=﹣190×5+1550=600,
∵k=﹣190<0,
∴p最大值小於600,
綜上:等待觀光車的遊客最多時有多少人620人.
八、(本題滿分14分)
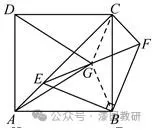
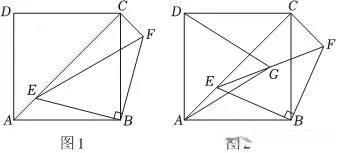
23.(14分)如圖1,點E是正方形ABCD的對角線AC上一個動點(不與A,C重合),連線BE,作等腰直角△EBF,其中∠EBF=90°,EF與BC相交,連線CF.
(1)求證:△ABE≌△CBF;
(2)如圖2,點G為EF的中點,連線DG,AG,DG=DC.
①△ADG是什麽特殊三角形,並說明理由;
②線段BE與CF之間的有什麽數量關系,並證明你的結論.
【解答】解:(1)∵四邊形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△EBF是等腰直角三角形,
∴BE=BF,∠EBF=90°,
∴∠ABC﹣∠EBC=∠EBF﹣∠EBC,即∠ABE=∠CBF,
在△ABE和△CBF中,
∴△ABE≌△CBF(SAS);
(2)①連線CG,BG,
∵四邊形ABCD是正方形,
∴∠BCA=∠BAC=45°,
∵△ABE≌△CBF,
∴∠BCF=∠BAC=45°,
∴∠ECF=∠BCA+∠BCF=90°,
∵點G為EF的中點,∠EBF=90°,
∴∠GCB=∠GBC,
∴∠GCD=∠GBA,
在△DCG和△ABG中,
∴△DCG≌△ABG(SAS),
∵DG=DC,AD=CD,
∵△ADG是等邊三角形;
∴∠GCB=90°﹣∠DCG=15°,
∵點G為EF的中點,∠EBF=90°,
∴△CGF是等邊三角形,
∴GE=GF=x,則EF=2x,
∵△EBF是等腰直角三角形,