沒想到是個科研人員提的問題,還問的這麽具體,那我簡單從嚴謹(瞎扯)的角度說一下。作為紅警營長水平,經驗還是不少的,還是有資格講講這個。
紅警2坦克交戰的唯象動力學:蘭開斯特方程式方法
一童天下*1
1物理系,b乎,地球,銀河系
ABSTRACT
In this Letter, 我們用蘭徹斯特戰鬥學理論討論了紅警中坦克隊形與數量的影響,建立了描述部隊戰鬥力的唯象理論。用這一方法可以簡潔明了的解釋為什麽一字長蛇陣會出現奇怪的戰損比。灰熊坦克和犀牛坦克實際的價效比is also investigated. 我們也給出了改善玩家紅警坦克操作表現的建設性建議。It is anticipated that our results would constitute an indispensable component of nonequilibrium statistical physics for RedAlert2.
1*https://www. zhihu.com/people/yi-ton g-tian-xia-86-69
I,Introduction
紅色警戒2是風靡全球的即時戰略(RTS)遊戲,與星際爭霸,魔獸世界,帝國時代並稱為RTS遊戲四大名著。即使遊戲已經釋出超過20年,遊戲的發行商westwood已經被收購,紅色警戒2還是在中國有不小的熱度。近年來,紅警HBK08,紅警魔鬼藍天等b站up主的視訊廣受歡迎,前者充電量甚至一度沖擊上b站第一。紅色警戒2遊戲視訊的爆火吸引了很多新手玩家重溫這款經典遊戲。但是RTS遊戲都有較高的門檻,很多玩家無法適應。這其中一個很fundamental的問題就是,為什麽同樣坦克數量交戰,總有一方會輸?
In this Letter,我們引入局部作戰區域的概念。將整個坦克交戰簡化為若幹局部交戰在時間上的累計。這些局部交戰的集合,就相當於是某種系綜。為了討論動力學,我們引入了 classical蘭開斯特戰鬥學方程式來唯象分析這類問題。Throughout this paper,我們主要考慮蘭開斯特平方律成立的情況。
II,坦克隊形的定量分析
很多人看到為什麽雙方坦克數量差不多,可以打出驚人的戰損比時感覺不可思議(08視訊彈幕,奇損現=奇怪的戰損比出現了),這裏面除去操作(點殺,殘血後拉),坦克品質(你灰熊怎麽可能打得過犀牛),血量(被放射線燙了一次什麽的)這些區別,最大的決定性因素就是坦克的隊形。
為什麽隊形這麽重要呢?很多人不理解。實際上很簡單,雖然坦克是個現代武器,但是在紅警裏面坦克的射程其實非常近(只有幾個車身的距離),所以實際上兩軍交戰的時候,處於作戰狀態的坦克數量是非常有限的。而真正決定此時誰會虧的,是這個 作戰狀態局部範圍內的勝負 情況。所以結論就很明確了,一字長蛇陣中,比如下圖紅方。看似紅藍雙方都是16個坦克,但是在交戰區域綠色圈裏面其實是8v4,顯然藍色贏。然後紅色後面的坦克進場還是面臨以少打多這樣的狀況。以此類推, 全程紅色都是在以少敵多。 自然紅色會輸了
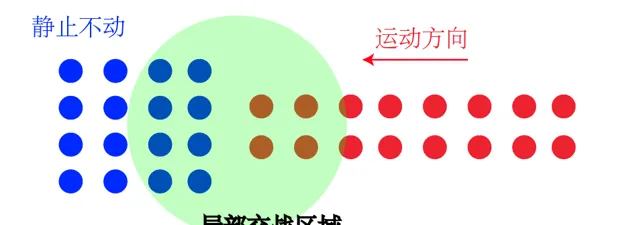
所以我們看到,真正決定勝負的其實並不是絕對的數量,而是每一個瞬間局部交戰的情況。將這每一個瞬間局部交戰的得失積分,看誰先消耗到0誰就輸了。實際上操作的坦克的時候往往也會遇到不小心一下子一字長蛇了,之後還得調整過來,但是一開始還是要吃虧。
知道了這個原理,題目裏面說「一字長蛇」是不好的隊形,這就是不嚴謹了,不好也是看相對於誰不好
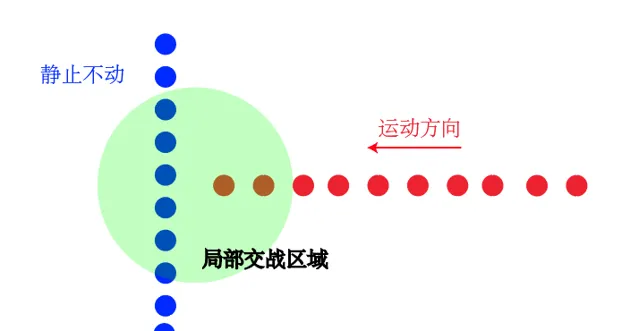
同樣是一字長蛇陣,猜猜看哪一方會贏?
至於局部交戰時候,到底數量的差異會有多大。我們用如下簡單理論分析,假設雙方坦克數量分別用 x(t) 和 y(t) 表示,我們很合理的假設一方坦克單位時間的減少量,應該是正比於對方坦克的數量的(敵人越多火力越猛,我們人也死的越多),就有
\frac{\mathrm d}{\mathrm d t}x(t)=-ay(t)
以及
\frac{\mathrm d}{\mathrm d t}y(t)=-bx(t)
這裏 a,b 都是正的常數,可以用來代表 y,x 隊伍的單個坦克的戰鬥力。
這個方程式組我相信物理系學生都很熟悉,這種互為求導關系的方程式在多自由度振動,電動力學等等很常見。為了方便讀者我還是詳細得寫一下,易得
bx(t)\frac{\mathrm d}{\mathrm d t}x(t)-ay(t)\frac{\mathrm d}{\mathrm d t}y(t)=0
也就是
\frac{\mathrm d}{\mathrm d t}[bx^2(t)-ay^2(t)]=0
說明 bx^2(t)-ay^2(t) 是守恒量,那麽有
bx^2(t)-ay^2(t)=bx^2(0)-ay^2(0)
其中 x(0),y(0) 代表初始時候的隊伍數量。我們假設雙方都是一樣的坦克,那麽 a=b ,初始的格局是4打5,看起來差別不大吧?帶入 x(0)=4,y(0)=5,x(t_{\rm final})=0 進去,看看 x 隊死光的時候 y 隊還剩多少?結果發現
y(t_{\rm final})=3
沒想到僅僅是多了一個坦克,居然結果是可以剩下來三個!這就是蘭開斯特平方關系,其實戰鬥力是和隊伍數量(在一定的假設下)的平方成正比的。所以數量差距會被平方一樣的放大。在上面第一張圖的例子中,8打4的情況下,可以剩下來 \sqrt{8^2-4^2}\sim6.9 大致七個,基本上也就沒失真失。持續下去,當然就是「奇怪的戰損比出現了」
紅警是一個規則簡單的遊戲,上面的討論適合於雙方都是一樣的坦克(比如都是0級犀牛),出場都是滿血,沒有帶狗的情況。這是很常見可以滿足的。
那如果是犀牛打灰熊呢?顯然此時 a\neq b 。但是他們到底比值是多少?這也可以反向運用蘭開斯特平方率求出,根據經驗(參見操作水平相同的情況下,同等價格的犀牛坦克和灰熊坦克誰更厲害?),犀牛與灰熊戰損交換比可以近似為 1:1.5 ,那麽相當於是說 x(0)=1,y(0)=1.5,x(t_{\rm final})=0,y(t_{\rm final})=0 ,解得 b/a=2.25 ,也就是說從經驗反推出犀牛的有效戰鬥力超過灰熊的兩倍!要知道犀牛900,灰熊還要700(甚至加了工業工廠打折後犀牛只要675更加便宜),所以說灰熊是真正的垃圾兵種,價效比極低。
當然至於為什麽灰熊這麽差,這裏有很多分析,我覺得比較合理的有,紅警2的不平衡性有哪些? 。也可以看我的分析操作水平相同的情況下,同等價格的犀牛坦克和灰熊坦克誰更厲害?
III,隊形最佳化分析
那麽在遊戲過程中,如何才能操控好隊形呢?這裏就不扯理論了,只說幹貨
1,交戰前調整坦克聚集到一塊,操作:框起來全部a一下地板(對動員兵這招尤其有效)
2,移動坦克的時候不要一下子點很遠,要一點一點移動,紅警2的尋路演算法是有問題的,拖動很遠很容易變成一字長蛇
3,不要過橋和別人打,不要硬沖狹窄路口
4,交戰前把狗移動到坦克前方,逃跑時移動到坦克後方,抗傷害
5,移動坦克的時候盡量左右或者上下平移,斜著移動不容易保持隊形
6,把1星,3星坦克移動到隊伍中間,不要一上來就被別人點死了
IV,Summary
To conclude, 我們使用了蘭開斯特戰鬥學方程式分析紅警2中坦克對戰的關鍵因素,並給出了動力學方程式。As a future prospect, 我們還需要討論坦克升級,帶狗,有動員兵,有地堡,有放射線工兵時候的坦克交戰情況。並借助蒙地卡羅模擬,分子動力學模擬的技術討論紅警中的坦克交戰問題。
Reference
本文不需要任何參考文獻










