作為一個名叫R2但還沒寫過幾個星戰的回答的答主,在這裏回顧一下星際大戰(新正史)影視系列中人類一時半會兒是肯定達不到的科幻設定。

1. 超空間跳躍
因為這是一個long long ago, and a galaxy far far away的時間地點,飛船不能超空間飛行的話同眾多科幻作品一樣,主角團從一個星球遊歷另一個星球,那大部份時間都浪費在路上了。。。這肯定不行。
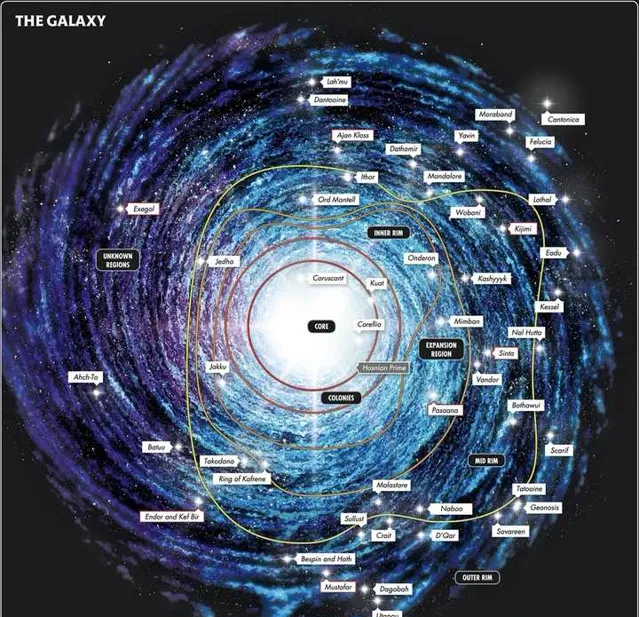
The galaxy | Wookieepedia | Fandom
例如,Han Solo引以為傲的:
漢:「我用十二個秒差距就完成了科舍爾航線。」丘巴卡:「嗷嗷嗷……」
漢:「你四舍五入一下就不是。」
——漢·索羅與丘巴卡向歐比-旺·克諾比、盧克·天行者自我介紹 [1]
漢以他高超的開船技術,完成科舍爾航線時透過的距離略多於12秒差距,而其他飛船則至少要透過20秒差距以上的距離。
我們知道1秒差距(pc)=3.26光年(ly),一艘 接近光速 飛行的飛船(比如v=0.9c )飛行12pc,或者大約 L= 40光年,如果沒有電腦計算超空間航道然後jump的話,塔圖因慣性系上的盧克看到(假設可以看到)千年隼勻速飛過去用了 T=40/0.9=44 年。
對於飛船上的漢和楚巴卡,由於相對論效應,世界線縮短為 \Delta L=\sqrt{c^2-v^2} T = 0.4cT [2] ,飛船的時間過去了\Delta\tau=\frac{\Delta L}{c}=0.4T ,也就是18年。(感謝評論區提醒,飛船參考系的時間會短一些)
年輕帥氣的漢人到中年,

等著他的盧克成為自暴自棄的老頭

盧克如果等不下去了,給漢打了個電(磁波)電話,還是得40年,這時漢也該老了,太費時間了。

超空間跳躍則是先設定好航線,從一個地方跳入,看到的恒星都拉線了

剛好東南路易士安那大學的助理教授Rhett Allain計算了在jump過程中,千年隼號的加速度。透過 【帝國反擊戰】 結尾,千年隼跳躍到超空間的鏡頭 [3] ,

假設千年隼號寬 25 米,從距離相機 100 米的距離開始,可以測量出千年隼的視角變化。
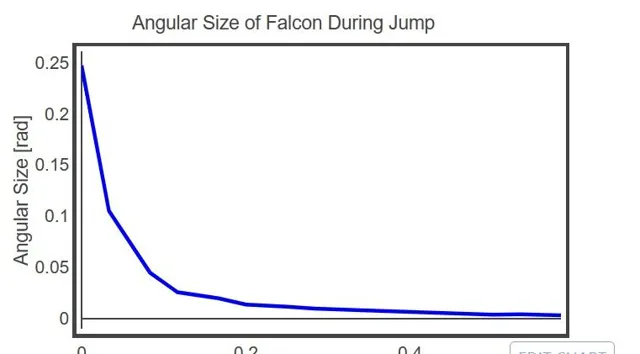
乘上相機距離即為千年隼在這段時間航行的距離
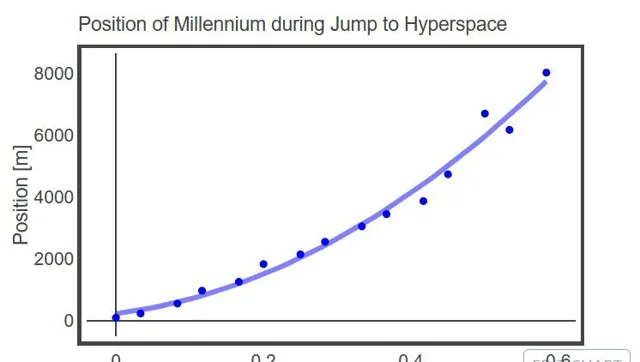
0.6s走了大概8km,由簡單的高中物理, x=x_0 + v_0t + \frac{1}{2}at^2 ,這個加速度擬合,Rhett算出來
\begin{align} a &= 33,922 \ \mathrm{m · s^{-2}} \\ v_0 &= 2977 \ \mathrm{m · s} \\ x_0 &= 234 \ \mathrm{m} \end{align}
這個加速度已經是3000多倍重力加速度了,對於需要進入深海狀態的「自然選擇,前進四」,加速度也才120G [4] ,所以為了讓主角團不變成肉泥,千年隼上得配備慣性阻尼器(inertial dampers)來抵消強大的慣性力。
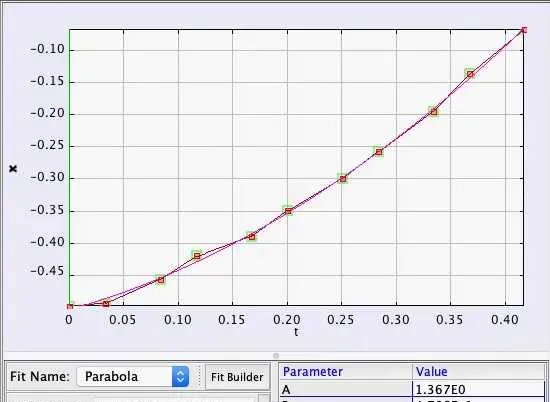
Rhett測量了在飛船內翻滾的R2(啊,翻滾的我?),用一個二次函式擬合,得到加速度是 a = 2.7 \ \mathrm{m · s^{-2}} ,大概0.3G的加速度,很友好。
進入超空間後,我們有可能碰到若隱若現的普爾褶鯨(Purrgil),普爾褶鯨天生就有超空間躍遷能力。據說,幾千年前,科學家們正是透過仿生學研究普爾褶鯨才發明了超空間驅動器 [5] 。

通常,匆忙地跳入hyperspace是危險的,正如【沙丘】中需要服用香料的領航員的預知能力才能完成星際航行一樣,星際大戰中超空間航行非常精密,所以Han Solo在超空間中僅用12pc就透過了阿卡德漩渦確實厲害。
在美劇【阿索卡】之前,飛船們只是在這個galaxy中(即有著宇宙中心塔圖因的星系)跳來跳去,這次終於用了個超大的超空間環跳到了其它星系,順便把發福的索隆元帥弄回來。

2. 死星
死星,Death Star,就是R2的圓形滑鼠墊,

New bing說
死星是帝國最強大的武器,它是一個巨大的人造衛星,能夠發射出足以摧毀一顆行星的雷射束。這種武器的威力是驚人的,但是它也需要消耗巨量的能量。如果要摧毀一顆行星,以目前地球人的水平顯然是不夠的,拿核彈狂轟亂炸也就在小破球裏炸個月亮(月亮:我招誰惹誰了qwq)。即使「核」平地球,頂多毀掉生物圈,地球還是好好的,不會像Leia公主家一樣

根據一些估算,要摧毀一顆地球品質( 6\times10^{24}\rm{kg} )的行星,或者說使這些粒子不再被束縛, 需要要克服地球的 重力結合能 (gravity binding energy) [6] ,
\display style{ U = -\frac{3GM^2}{5R} }
這個系數是怎麽來的,R2可以簡單講一下,當然 [6] 中已經有推導了,思路很簡單,品質 \mathrm{d}m 的球殼的重力勢能是 \display style \mathrm{d}U = -\frac{GM(<r)}{r}\mathrm{d}m=-\frac{4}{3}\pi r^3\rho \ \frac{G}{r} \ 4\pi \rho r^2\mathrm{d}r=-\frac{16}{3}\pi^2 G\rho^2 r^4{d}r
然後對所有球殼積分, \display style U = -\frac{16}{3}\pi^2 G\rho^2 \int_0^R r^4{d}r = -\frac{16}{15}\pi^2 G\rho^2 R^5
前面假設的均勻密度的球,總品質 M=\frac{4}{3}\pi R^3\rho 代進去就得到上面簡潔的運算式了,一個簡單的高數題。
地球半徑大約是6370km,得到 U=2.24 \times10^{32} \rm{J} 。考慮地球密度的不均勻,實際的U在 2.49 \times10^{32} \rm{J} [6] 。
太陽每秒發出的能量是 10^{26} 焦耳量級,相當於死星轟出地球的重力結合能這麽多能量相當於10天的太陽能量,人類顯然達不到。所以New bing說,
死星需要有一個非常高效和穩定的能源系統(R2說,是 凱伯水晶 ),而且還要考慮到雷射束在空間中傳播時會損失多少能量。因此,死星超級武器是一種超出人類能力範圍的設定,人類目前沒有任何技術能夠制造出這樣的武器。下面幾個圖是死星在工作,比如,俠盜一號中的熱帶星球Scarif

或者死星的早期測試,毀掉Jedha古代聖城

都出現了綠色雷射。設定裏死星用的是超級雷射炮,設計功率是 6.2\times10^{32} \rm{J/s} [7] 。在新希望結尾中被盧克炸了後,帝國搞了死星2號,結果在絕地歸來中又毀掉了,直到蕾伊ppt去死星2號廢墟尋找西斯wayfinder,死星才再度出鏡。
至於達斯米契推出的 弒星者基地 Starkiller Base是一個行星改造的,「利用恒星的能量來收集暗能量」 [8] ,所謂可以直接摧毀一個恒星系。

好吧,越來越扯,如果盧克失敗了,帝國喪心病狂想摧毀一顆太陽,甚至摧毀整個「銀河系」呢?
建議把舊正史的遇戰瘋人拉過來打一架。
3. 還想寫啥
R2想湊個第三點,但是發現前面寫的不少了,其實星戰中的不少東西已經在現實中有了一些近似的實作,比如R2機器人
很多星戰機器人愛好者會加入的R2建造者俱樂部
這裏有很多我的同類機器人朋友們。
至於可以烤肉的light saber(我們記得它叫 光劍 ,不是雷射劍!!!),也有了神還原。

最後以GPT的話結束。
以上就是星際大戰中人類科技水平無法實作的設定,當然,這並不影響我們欣賞這部電影的魅力和創意。科幻電影的目的不一定是要展示真實的科學,而是要激發我們的想象力和探索精神。也許有一天,人類能夠突破現有的科技限制,實作星際大戰中的一些設定,但在那之前,我們可以透過電影來體驗一個不同的世界和故事。就醬。(獎勵星戰的閱讀量
歡迎關註R2的專欄:予日行辰,不定時更新。。。

分類整理:天文、Linux、編程、雜談、科幻、科研、醫學流水賬
本文最早發於2023.10.28
參考
- ^ 科舍爾航線 https://starwars.fandom.com/zh/wiki/科舍尔航线
- ^ 這裏的計算更詳細,也復雜 https://www.zhihu.com/question/436831676
- ^ The Physics of the Millennium Falcon's Jump to Hyperspace https://www.wired.com/story/the-physics-of-the-millennium-falcons-jump-to-hyperspace/
- ^ 【三體】中行星際飛船「前進四」的加速度至少有多大? https://www.zhihu.com/question/35541698
- ^ 南大的【曼達洛人】第三季第1集細節解析 https://zhuanlan.zhihu.com/p/610923606
- ^ a b c Physics:Gravitational binding energy https://handwiki.org/wiki/Physics:Gravitational_binding_energy
- ^ Death Star wiki https://en.wikipedia.org/wiki/Death_Star
- ^ Starkiller Base https://starwars.fandom.com/wiki/Starkiller_Base











