中國高等教育的數學課都是數學系老師教的,乍一看天經地義,但實則數學系老師只會用純數學的思維教課,只說定義、性質,再用剩下的兩節課證明性質,從不說這些花花綠綠公式是幹什麽用的,才會催生出一大批和題主一樣的對學數學產生懷疑的人。
數學是可以用並且非常實用的學科!
尤其是矩陣
1.1、影像處理
先說最簡單的灰度圖,影像是由一個個小像素點行列排列組成的,每個像素點由數值大小代表不同顏色(黑白灰),那麽圖片天然就可以用一個矩陣表示。把一張黑色的圖片和一張白色的圖片摻雜變成灰色的圖片,說白了就是(1+0)/2=0.5的過程,矩陣表示為:
C=(A+B)/2
如果不用矩陣:
c_{11}=( a_{11} +b_{11})/2
c_{21}=( a_{21} +b_{21})/2
`
`
c_{mn}=( a_{mn} +b_{mn})/2
一張圖怎麽也得幾百個像素點吧。這還只是黑白灰圖片,彩色圖片是由紅綠藍三個通道組成的,那就是三維矩陣了,換成普通運算式又得翻3倍。
小米釋出了一億像素的手機,不知道題主對一億有沒有概念,如果鋪成可愛的脖子長長的小動物可以繞內心一圈。
但矩陣運算式永遠都是簡單的(再寫一遍):
C=(A+B)/2
1.2、影像壓縮
老師肯定講過特征值分解後,較大的幾個特征值包含了原矩陣更多的資訊,剩下的幾個特征值越小,對原矩陣貢獻越小。
基於此,對於一張一億像素的圖片,應該可以理解保存在磁盤上是非常大的一個檔,進行奇異值(只有方陣才有特征值,非方陣叫奇異值)分解後,只留下特征值較大的,以及對應的特征向量,剩下的全部扔掉,就可以完成影像壓縮,減小磁盤占用,而不影響圖片的辨識度。
如果不用矩陣。。。想不出來了,大概就像按元素寫SVD分解吧,可能類似給一億只小動物逐個起名字吧。
2、空間變換
機器人座標變換盡管爛大街了,鑒於讀者專業不同,說個容易理解的:衛星在太空把天線朝向從西安轉移對準北京(這裏只是用來說明旋轉變換的容易理解的例子,真實航空航天是怎樣算的並不知道):
v_1=Rv_0
其中R是旋轉矩陣, v_0 為衛星當前朝向向量(對準西安), v_1 為目標朝向向量(對準北京)。
在這裏不嚴格推導了,我們定性分析一下,繞空間三個自由度旋轉,每個座標旋轉後都會影響下一個座標位置的選取,所以數學上就是一大堆三角函式相乘,類似於: x_1=cos\alpha *cos\beta *x_0 + (sin\gamma *sin\alpha * cos \beta -cos\gamma*sin\beta)*y_0+(cos\gamma *cos\alpha * sin \beta -sin\gamma*cos\beta)*z_0
y_1=cos\alpha *sin\beta *x_0 + (sin\gamma *sin\alpha * sin \beta +cos\gamma*cos\beta)*y_0+(cos\gamma *sin\alpha * sin \beta -cos\gamma*cos\beta)*z_0
z_0=-sin\alpha*x_0+sin\gamma*cos\beta*y_0+cos\gamma*cos\beta*z_0
x、y、z為朝向向量v的三個方向分量。
3、最小平方
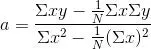
線性回歸常用公式,中學統計題中求斜率經常見到,表面看似簡單的公式,但裏麵包含了數個求和符號:和的平均、平方和的平均、和的平方的平均、積的和的平均,和的積的平均,當時為了算這個公式內心不知跑過多少長脖子的小動物。之後有了多元函式、高次函式擬合約樣是基於最小平方原理,更加mmp。但他的矩陣形式:
b=(X^TX)^{-1}X^Ty
內心的小動物瞬間安靜了。
4、空間約束
這個在最佳化問題比較常見,比如初中就學過開口向上的二次函式最小值在槽底,但如果限定x取值範圍的話,槽底可能根本不在所規定的可行域範圍內。
如果不是初中的二次函式,而是高維空間,自變量有上百個,他的可行域空間約束:
x_1+3x_2-0.2x_3+...+mx_n<2
x_1-3x_2+10x_3+...+ax_n<0.6
`
`
8x_1-0.2x_2+1.6x_3+...+cx_n<22
寫成矩陣:
Ax<b
搞定。
5、卡爾曼濾波
卡爾曼濾波是控制理論對系統狀態估計最常用的方法,矩陣形式:

其中中有一個求增益K的公式,也就是第三個公式,註意分母也是矩陣(眾所周知矩陣不存在除法,分母實際是右乘他的逆)
如果不用矩陣,其他幾個公式尚且可以按元素乘開,但唯獨這個K,總不能把矩陣求逆按元素展開寫進程式碼裏吧,那樣心裏可就不止幾只可愛的小動物那麽簡單了。。。
===========
依稀記得書上說特征值在工、醫、化、生、經等各個學科有極其廣泛的套用,但無論是課本還是數學系老師對這個''極其廣泛''到底怎麽廣泛卻只字不提。等到後來實踐接觸越多,才發現矩陣理論真如王八拳一樣可以打遍天下無敵手,但因為數學系老師當初的填鴨教育,好多東西必須回頭再學一遍。
因此在此對矩陣理論產生懷疑的讀者們保證一句: 矩陣理論,絕對有用,絕對好用。
數學有一個特點,它可以完成數學體系內的自洽而不與外部世界發生交集,其他學科諸如物理化學電腦醫學生物歷史經濟等,則必須依靠現實世界進行推演,馬克思說萬物都是物質的,但數學除了要寫在物質上要人理解以外,好像真的可以完全脫離物質。
數學系老師也有一個特點,他們追求純數學裏的自洽,沈浸在數學性質證明上,而完全脫離數學性質在現實世界的套用。
小學學數學,是和小明小紅一起度過的。
大學學數學,只能和內心的脖子長長的小動物一起度過了。
希望工科數學改革,讓工科系老師教數學。哪怕讓小明和小紅回來也好哇。
=========
哈哈哈哈,已經越來越多的人開始同情背鍋的數學系老師了。我必須澄清一下,我認為理論數學是極其具有前瞻性的學科,量子物理的發展就以早就存在但當時看似無用的理論數學為基礎的。研究理論數學的人更是這個星球上最聰明的人的集合。我吐槽的是高等教育數學課的教學模式,畢竟教學大綱裏沒有數學套用人家老師自然也不必講。
張躍輝老師那本【矩陣理論與套用】每一章最後一節都在寫本章內容的實際套用,可上課的老師只會背對講台在那裏證明性質123而絕口不提套用123。不能說數學系老師不懂工科套用,因為考試大綱裏沒有啊,正課都講不完還拓展什麽?套用書上有寫你自己去看就好了啊?
話說回來,雪崩前沒有一片雪花是無辜的。但前邊性質推導我也能自己看也不用講啊?正是因為學生缺乏實踐經驗,所以套用部份才需要有經驗的人來講啊?
我計算方法那門課老師是工科背景的,微分方程式旁征博引,希望數學系老師都去聽一聽。
==================
祈求喜歡無腦噴的知友提升一下閱讀理解能力 T_T,幫這類人概括一下中心思想:
- 題目問的是''簡化'',所以我舉得是簡化表達的例子。
- 吐槽的是工科數學的授課模式,不是數學系,詳見京東連結上一段。
當然絕大部份知友都是能夠理解的,畢竟數學課不提原因就講性質轉眼就考試太有共鳴了。









