用 【幾何原本】 中的話說,就是「三等分一般角是立體問題,不是平面問題」。
本書對作圖問題的復雜程度進行了兩次分類:第一次是按產生所需交點需要直線的條數分類,將4條直線以內的問題稱為「 平面問題 」,5~8條直線則為「 立體問題 」,9條以上直線為「 超立體問題 」。第二次是按表示所求長度所需可巢狀方程式的最高次數分類(系數為以已知長度或任意有理數,「巢狀」指方程式的根可作另一方程式的系數,例如已知a、b求作x,且 t^2+at+b=0 ,x=a+t,則最高次數為二次),低於二次為「 平面問題 」,三至四次為「 立體問題 」,五次以上為「 超立體問題 」。
相比較而言,第一種分類比較抽象,不容易理解。所以後人在利用這些結論時,主意采用第二種分類方法,即由巢狀方程式的最高次數判斷。
平面問題 有一個重要的特點,即可以透過通常的(只在 平面內 使用無刻度直尺和康伯斯)尺規作圖作出;反之,立體問題與超立體問題都不能尺規作圖。證明方法需要用到群論,這裏不作展開。平面問題的得數也存在一個特征:可以由已知數、有理數作四則運算或開 平方根(或2^n 次方根) 運算得到。例如,已知a、b、c,則 \frac{1+2\sqrt{ab}}{3} 、1+\sqrt{a+3\sqrt{b^3-c}} 等為平面問題;而 \frac{3+\sqrt[3]{2a}\cdot b}{4a}+c^2 則是立體問題,因為出現了立方根。
由「 立體問題 」定義易知,將平面問題得數的特征中增加「 開立方根(或 2^n\cdot3^m 次方根) 」的允許操作即立體問題。但 【幾何原本】中對於「立體問題」的描述為:可以在立體空間中透過尺規作圖得出。 根據三倍角的余弦公式,顯然 三等分任意角是立體問題 。題主所用的方法中,將所作扇形 在空間中制成立體圖形——圓椎 ,本質上就是 在空間中 利用尺規作圖。根據本描述,利用這一類作圖方法一定能作出立體問題,但本書的關註點不在此,未作展開。
本書中取而代之的是 截線法 ,即用立體可作圖形在平面上的截線,在平面內作圖,以解決立體操作的不方便性。因為圓錐是立體可作圖形(就像題主利用的方法),它與平面的截線為圓錐曲線,故可以用圓錐曲線作出立體問題。需要註意的是,這裏的圓錐曲線只能選取橢圓(不包括圓)、拋物線、雙曲線(屬於立體可作而平面不可作的圖形),而不能選取平面可作的圓和雙直線。相比較之下拋物線的方程式較簡單,故本書中以 拋物線 為例。
以下是開立方根的方法:首先在座標系中作出拋物線 y=x^2 ,並取點(0,1)為A。過A點作水平線AB,且 AB=\frac{a}{2} 。以B點為圓心,以OB為半徑作圓,交拋物線於O、C兩點。過C點作水平線CD,交y軸於點D,則 CD=\sqrt[3]{a} 。
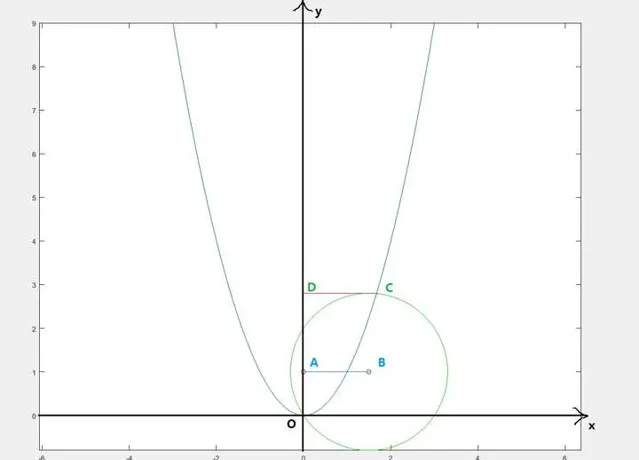
更一般地,如果求作x使 x^3=ax+b ,則令A點座標為 (0,1+\frac{a}{2}) ,B點座標為 (\frac{b}{2},1+\frac{a}{2}) ,其余不變。特別地,若已知角的余弦值為 cos\theta=a ,根據三倍角公式,則令 A(0,\frac{11}{8}) , B(\frac{a}{8},\frac{11}{8}) ,作出的CD長度即 cos\frac{\theta}{3} ,從而實作三等分角。
本描述實際上存在一個問題, 對「立體問題」的界線不明確 。因為正五邊形可尺規作圖,故利用題主的方法可以五等分任意角,從而五等分任意角是 立體問題 。但如果設 cos\theta=a , sin\theta=b ,其中θ可任意取值,則顯然cos\frac{\theta}{5}=\frac{\sqrt[5]{a+bi}+\sqrt[5]{a-bi}}{2} 用到了五次方根,按照本書的描述其實屬於 超立體問題 。從而產生矛盾的結論。











