比如用機器學習演算法來預測學習者的長期記憶。機器學習是電腦科學下的一個分支,而長期記憶屬於認知心理學下的一個熱門研究方向。
可能有人會問,預測學習者長期記憶有啥用。我打個比方,在戰爭中,能夠精確預測炮彈落點的一方,能夠用更少的火炮,打擊更多有價值的目標。在學習中,如果我們可以精確預測一個人所知的一切知識的記憶情況,我們就能制定相應的高效學習策略,用更少的時間記住更多的知識。
現在比較公認的、有實證研究支持的高效記憶方法叫做間隔重復(spaced repetition),這在心理學的學術界已經有很多研究了,比如下面這篇綜述:

但是在傳統心理學研究中,研究者透過設定實驗能夠收集到的數據非常有限,難以建立有關長期記憶的精確模型,更不用說設計高效的間隔重復演算法了。不過現在已經有不少開源的大規模記憶數據集,比如:
有了這些數據,就可以對人類記憶進行建模。這裏簡單介紹一下我在這個領域的研究進展。
數據收集
數據是記憶演算法的源頭活水,沒有數據,巧婦也難為無米之炊。收集合適、全面、精確的數據,將決定記憶演算法的上限。
為了精準的刻畫學習者的記憶情況,我們需要定義出記憶的基本行為。先讓我們思考一下,一個記憶行為,包含哪些重要內容?
最基本的要素很容易想到:誰(行為主體)何時(時間)做了什麽事(記憶)。對於記憶,我們又可以繼續挖掘:記了什麽(內容)、記得怎麽樣(反饋)、花了多久(成本)等等。
考慮到這些內容之後,我們便可用一個元組來記錄一條記憶行為事件:
e:=(user,item,time,response,cost)
該事件記錄了一個使用者 user 對某條材料 item 在某個時刻 time 作出了某類反饋 response,付出了多少成本 cost。舉例說明:
e:=(\textrm{小葉},\textrm{apple},\textrm{2022-04-01 12:00:01},\textrm{忘記},\textrm{5秒})
即:小葉在 2022 年 4 月 1 日 12 點 0 分 1 秒記憶了 apple 這個單詞,反饋忘記,用時 5 秒。
有了基本的記憶行為事件的定義,我們在此基礎上,抽取、計算更多感興趣的資訊。
比如,在間隔重復中,兩次重復之間的時間間隔是一個重要的資訊,利用上述記憶行為事件,我們可以將事件數據按照 user、item 分組,按 time 進行排序,然後將相鄰兩次事件的 time 相減,即可得到間隔。通常來說,為了省去這些計算步驟,可以直接將間隔記錄在事件中。雖然造成了儲存冗余,但能夠節省計算資源。
除了時間間隔之外,反饋、間隔的歷史序列也是一個重要的特征。比如「忘記、記得、記得、記得」、「1 天、3 天、 6 天、10 天」,這些資訊能夠較為完整地反映一個記憶行為的獨立歷史,也可以直接記錄到記憶行為事件中:
e_{i} :=(user, item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}} , \Delta t_i , r_i)
DSR 模型
有了數據之後,該如何利用呢?其實我們想要知道的是記憶狀態的種種內容,而我們目前收集的數據暫時不包括這些內容。因此,如何將記憶數據轉換成記憶狀態和狀態之間的轉移關系,是本節的目標。
記憶狀態
DSR 模型的三個字母分別對應難度(difficulty)、穩定性(stability)和可提取性(retrievability)。讓我們先從可提取性入手。可提取性反應了記憶在某時刻的回憶機率,但記憶行為事件已經是進行回憶後的結果。用機率論的語言來說,記憶行為是只有兩種可能結果的單次隨機試驗,其成功機率等於可提取性。
因此,若要測得可提取性,最容易想到的方法就是對同一個記憶進行無數次獨立實驗,然後統計回憶成功的頻率。但這種方法在實際上是不可行的。因為對記憶進行實驗,將改變記憶的狀態。我們無法作為一個觀察者,在不對記憶造成影響的情況下對記憶進行測量。(註:以目前的腦科學水平,還無法在神經層面測量記憶的狀態,因此這條路目前也用不了)
那麽,我們就束手無策了麽?目前有兩種妥協的測量方式:(1)忽略記憶材料的差異:SuperMemo 和 Anki 都屬於此類;(2)忽略學習者的差異:MaiMemo 屬於此類。(註:其實作在已經考慮了,只是在我剛動筆寫這段話的時候還沒開始考慮,但是沒有關系,不會對理解下面的內容產生影響)
忽略記憶材料的差異是說,測量可提取性時,統計除了記憶材料外其他內容都相同的數據。雖然無法對一位學習者、一條材料進行多次獨立實驗,但一位學習者、多條材料就可以了。而忽略學習者的差異,則是對多位學習者、一條材料進行統計。
考慮到 MaiMemo 的數據量較為充分,本節僅介紹忽略學習者差異的測量方式。忽略後,我們便能聚合得到新的記憶行為事件組:
e_{i} :=(item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}} , \Delta t_i , p_i, N)
其中,N 為記憶該材料且歷史行為相同的學習者數量,可提取性 p=\frac{n_{r=1}}{N} 是這些學習者中回憶成功的比例。當 N 足夠大時,比率 n_{r=1}/N 接近真實的可提取性。
解決了可提取性之後,穩定性也就迎刃而解了。測量穩定性的方法是遺忘曲線,根據收集的數據,可以使用指數函式來回歸計算 (item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}}) 相同的記憶行為事件組的穩定性。
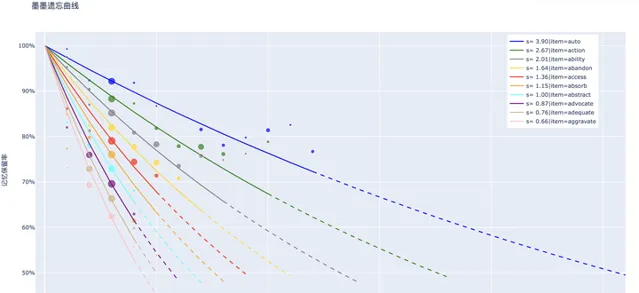
圖中的散點座標為 (\Delta t_i , p_i) ,相對大小為 \log N 。曲線是擬合後的遺忘曲線。
最後,該對難度下手了。如何從記憶數據中得出難度?讓我們先從一個簡單的思想實驗開始。假設有一群學習者,第一次記憶 apple 和 accelerate 兩個單詞。如何用記憶行為數據來區分兩個單詞的難度?
最簡單的方法,在第二天立即測試,記錄記憶行為數據,統計一下,看見哪一個單詞的回憶比例更高。從這一個立足點出發,我們可以將第二天的回憶比例,換成第一次記憶後的穩定性。
也就是說,第一次記憶後的穩定效能夠反映出難度。但如何使用第一次記憶後的穩定性來劃分難度,並沒有統一的標準。怎樣的劃分方式最好,也沒有定論。作為入門材料,本文就不詳細討論了。
狀態轉移
至此,我們已經可以將記憶數據轉化為記憶狀態:
(item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}} , \Delta t_i , p_i, N) => (D_i, S_i, R_i)
接下來,我們便可以著手描述狀態之間的轉移關系。如 (D_i, S_i, R_i) 在 \Delta t 天後復習,回憶結果為 r ,得到新的記憶狀態 (D_{i+1}, S_{i+1}, R_{i+1}) 。那麽,(D_{i+1}, S_{i+1}, R_{i+1}) 與(D_i, S_i, R_i) 和 \Delta t 、r 之間的關系是什麽?
首先,依然是先將記憶狀態數據整理成適合分析的形式:
(D_i, S_i, R_i, \Delta t, r, D_{i+1}, S_{i+1}, R_{i+1})
其中, R_{i+1} 在復習後會立刻達到 100%,因此在分析過程中可以將其忽略。還有R_i 、\Delta t 和 S_i 之間知二求一,可以忽略掉 \Delta t 。
最終,我們要分析的狀態轉移數據如下:
(D_i, S_i, R_i, r, D_{i+1}, S_{i+1})
而 \cfrac{S_{i+1}}{S_i}=SInc ,正好可以參考我們在記憶穩定性增長一章中的提到的幾個規律:
SInc = a S^{-b}
SInc = c e^{-d R}
可以得到關系公式(難度 D 的影響在此處被省略了):
S_{i+1} = S_{i} \cdot a S_{i}^{-b} e^{-c R_i}\textrm{(if r = 1)}
根據上式,我們預測學習者的每次回憶成功後的記憶狀態 (D_{i+1}, S_{i+1}) 。反饋遺忘也是同理,可以用另一組公式狀態轉移方程式進行描述。
SRS 模擬
有了記憶的 DSR 模型,我們便可以模擬任何復習規劃下的記憶情況。那麽,具體該如何模擬呢?我們需要從現實中普通人是如何使用間隔重復軟體的角度出發。
假如小葉需要為四個月後的考研英語做好準備,需要使用間隔重復記憶考研考綱英語單詞。而由於其他科目也需要抽時間準備。
從上面這句話中,有兩個很明顯的約束:學習周期天數和每日學習時間。SRS(Spaced Repetition System)模擬器需要將這兩個約束考慮進來,同時這也點明了 SRS 模擬的兩個維度:日間(by day)和日內(in day)。此外,考綱單詞的數量是有限的,所以 SRS 模擬還有一個有限的卡片集合,學習者每天都從這個集合中挑選材料進行學習和復習。而復習任務的安排則由間隔重復排程演算法來安排。整理一下,SRS 模擬需要:
- 材料集合
- 學習者
- 排程器
- 模擬時長(日內+日間)
其中學習者可以用 DSR 模型進行模擬,給出每次復習的反饋和記憶狀態。排程器可以是 SM-2、Leitner box、遞增間隔表,或者其他任何安排復習間隔的演算法。而模擬時長和材料集合則需要根據想要模擬的情況來設定。
然後,我們從 SRS 模擬的兩個維度出發,設計一下具體的模擬流程。顯然,我們需要按照時間順序,一天一天地往未來模擬,而每一天的模擬則由一張張卡片的反饋組成。所以,SRS 模擬可以由兩個迴圈組成:外層迴圈表示當前模擬的日期,內層迴圈表示當前模擬的卡片。在內層迴圈中,我們需要規定每次復習所花費的時間,當累計時間超過每日學習時長限制時,自動跳出迴圈,準備進入下一天。
SRS 模擬的虛擬碼如下:
 相關的 Python 程式碼我開源在了 GitHub 上,感興趣的讀者可以自行閱讀程式碼:L-M-Sherlock/space_repetition_simulators: 間隔重復模擬器 (github.com)
相關的 Python 程式碼我開源在了 GitHub 上,感興趣的讀者可以自行閱讀程式碼:L-M-Sherlock/space_repetition_simulators: 間隔重復模擬器 (github.com)
SSP-MMC 演算法
說完了 DSR 模型和 SRS 模擬,我們已經能夠預測學習者的記憶狀態和在給定復習規劃下的記憶情況,但是仍然沒有回答我們的最終問題:怎樣的復習規劃是最高效的?如何找到最優的復習規劃呢?SSP-MMC 演算法從最優控制的角度解決了這一問題。
SSP-MMC 是 Stochastic Shortest Path 和 Minimize Memorization Cost 的縮寫,以體現這一演算法的數學工具和最佳化目標。以下內容改編自我的畢業論文【基於 LSTM 和間隔重復模型的復習排程演算法研究】 [1] 和會議論文 A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling [2] 。
問題場景
間隔重復方法的目標在於幫助學習者高效地形成長期記憶。而記憶穩定性反映了長期記憶的儲存強度,復習次數、每次復習所花費的時間則反映了記憶的成本。所以,間隔重復排程最佳化的目標可以表述為:在給定記憶成本約束內, 盡可能讓更多的材料達到目標穩定性,或以最小的記憶成本讓一定量的記憶材料達到目標穩定性。其中,後者的問題可以簡化為如何以最小的記憶成本讓一條記憶材料達到目標穩定性,即最小化記憶成本(Minimize Memorization Cost, MMC)。
DSR 模型滿足馬可夫性,每次記憶的狀態只取決於上一次的記憶狀態和當前的復習輸入和結果。其中回憶結果服從一個與復習間隔有關的隨機分布。由於記憶狀態轉移存在隨機性,一條記憶材料達到目標穩定性所需的復習次數是不確定的。因此,間隔重復排程問題可以視作一個 無限階段的隨機動態規劃問題。考慮最佳化目標是讓記憶穩定性達到目標水平,所 以本問題存在終止狀態,可以轉化為一個隨機最短路徑問題(Stochastic Shortest Path, SSP)。
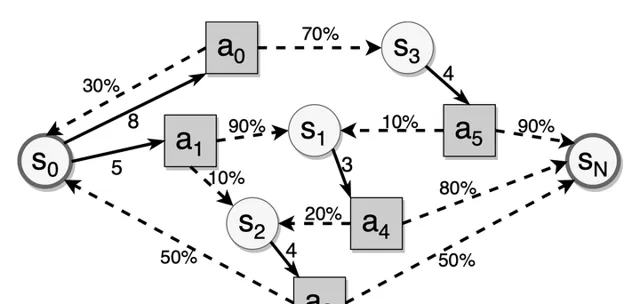
如上圖所示,圓圈是記憶狀態,方塊是復習行為(即當前復習後的間隔),虛線箭頭表示給定復習間隔的狀態轉移,黑邊表示給定記憶狀態中可用的復習間隔。間隔重復中的隨機最短路徑問題是找到最佳復習間隔,以最小化到達目標狀態的預期復習成本。
方法表述
為了解決這個問題,可以用馬爾科夫決策過程(MDP)來建模每張卡片的復習過程,有一組狀態 \mathcal{S} 、行為 \mathcal{A} 、狀態轉換機率 \mathcal{P} 和成本函式 \mathcal{J} 。演算法的目標是找到一個策略 \pi ,使達到目標狀態 s_N 的預期復習成本最小。
\pi^{*}=\underset{\pi \in \Pi}{\operatorname{argmin}} \lim\limits_{N\to \infty} E_{s_{0}, a_{0}, \ldots}\left[\sum_{t=0}^{N} \mathcal{J}\left(s_{t}, a_{t}\right) \mid \pi\right]
狀態空間 S 取決於記憶模型的狀態大小。DSR 只有兩個狀態變量,所以狀態可以表述為 s=(D,S) 。行為空間 \mathcal{A}=\{\Delta t_1,\Delta t_2,\cdots,\Delta t_n\} 由可以安排復習的 N 個間隔組成。狀態轉換機率 \mathcal{P}_{s,a}(s') 是卡片在狀態 s 和行為 a 下被回憶的機率。成本函式 \mathcal{J} 定義為:
\begin{aligned} \mathcal{J}(s_0) & = \lim\limits_{N\to \infty} E\left[\sum\limits_{t=0}^{N-1}g_t(s_t,a_t(s_t), r_t) \right]\\ r_{t} & \sim Bernoulli(p_{t}) \end{aligned}
其中 g_t 是每次復習的成本, r_t 是服從白努利分布的回憶結果。目標狀態 s_N 即目標穩定性所對應的狀態。
演算法設計
可以用值叠代方法來解決 \textrm{MDP}(\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{J}) ,其貝爾曼方程式為:
\begin{aligned} \mathcal{J}^*(s) & = \min\limits_{a \in \mathcal{A}(s)} \left[\sum\limits_{s'}\mathcal{P}_{s,a}(s')(g(r) + \mathcal{J}^*(s'))\right]\\ s' & = \mathcal{F}(s,a,r,p) \end{aligned}
其中 \mathcal{J}^* 是最優成本函式, \mathcal{F} 是狀態轉移函式,即 DSR 模型。對於每次復習的成本,出於簡單起見,只考慮回憶結果的影響: g(r) = a \cdot r + b \cdot (1-r) ,a 是回憶成功的成本,b 是回憶失敗的成本。
基於該貝爾曼方程式,下圖所示的值叠代演算法在叠代過程中使用成本矩陣來記錄最優成本,使用策略矩陣來保存每個狀態的最佳行為。

不斷遍歷每個記憶狀態下的每個可選的復習間隔,比較選擇當前復習間隔後的期望記憶成本和成本矩陣中的記憶成本,如果當前復習間隔的成本更低,就更新對應的成本矩陣和策略矩陣,最終所有記憶狀態對應的最優間隔和成本就會收斂。
這樣以來,我們便得到了最優復習策略,與預測記憶狀態的 DSR 模型相結合,便可為每一位使用 SSP-MMC 記憶演算法的學習者安排最高效的復習規劃。
更多相關研究資源,請見:
參考
- ^ [本科畢設] 基於 LSTM 和間隔重復模型的復習演算法研究 https://zhuanlan.zhihu.com/p/626308184
- ^ KDD'22 | 墨墨背單詞:基於時序模型與最優控制的記憶演算法 [AI+教育] https://zhuanlan.zhihu.com/p/577383961





